基于动态损失厌恶投资组合模型的最优资产配置与实证研究

金 秀，王 佳，高 莹

（东北大学工商管理学院，辽宁沈阳 110819）

基于动态损失厌恶投资组合模型的最优资产配置与实证研究

金 秀，王 佳，高 莹

（东北大学工商管理学院，辽宁沈阳 110819）

从行为金融学的角度考虑投资者损失厌恶的心理特征，建立预期效用最大化的动态损失厌恶投资组合优化模型。以我国股票市场为依托，将市场分为上升、下降和盘整三种状态，研究动态损失厌恶投资组合模型的最优资产配置和绩效表现，并与静态损失厌恶投资组合模型、M-V投资组合模型和CVaR投资组合模型进行比较。最后，在具有交易成本的条件下对动态模型进行稳健性检验。得出结论：不同情况下，动态损失厌恶投资者具有不同的最优资产配置比例，且动态损失厌恶投资组合模型明显优于静态模型、M-V投资组合模型和CVaR投资组合模型。

动态损失厌恶；资产配置；稳健性检验；前景理论

1 引言

一直以来，预期效用理论是研究投资决策的理论基础，描述理性经济人在风险环境下的资产配置行为。但是研究表明，该理论不能有效地解释金融市场上的各种异象。一些学者认为这是由于人类的认知、情感等心理因素严重地影响投资者的决策行为。Kahneman和Tversky［1］提出了著名的前景理论，从认知心理学的角度研究投资者的决策行为，指出人们具有损失厌恶特征对损失比对盈利更敏感。它是行为金融学最为重要的成就之一。

国内外一些学者对损失厌恶行为的特征进行研究，大多数工作主要集中于实验研究或模拟研究［2-7］。受诸多不可控因素的影响，实验中的决策者可能与其在真实金融市场中的表现不同，研究结果不具有完全可信性。随后，一些学者研究损失厌恶投资者的金融资产配置问题。Bernard等［8］研究单期经济体中累积前景理论投资者的最优投资组合选择。Berkelaar等［9］研究损失厌恶拐点幂效用函数下的最优资产配置，指出当评估期间较短时，具有损失厌恶特征的投资者在初始投资组合中股票的权重较少。De Giorgi［10］研究不同损失厌恶程度下狭窄框架对投资者资产配置决策的影响。Blake［11］将损失厌恶与固定缴款养老金计划相结合，研究基于目标导向的养老金的最优配置问题。Fortin等［12］研究了M-V投资组合模型、CVaR投资组合模型和线性损失厌恶投资组合模型具有相同最优解的条件，并对美国和欧洲股票市场进行了实证分析。Fong W M［13］指出前景理论价值函数值随着投资期间的增加而单调递增，而M-V最优资产配置策略则表现为保守投资，其股票的权重随着投资期间的增加而降低。徐绪松等［14］用投资者财富变化和期末最终财富表示投资者效用函数，建立了基于损失厌恶的最优投资组合模型，并对我国股票市场进行了实证分析。胡支军等［15］从期望效用最大化的角度建立了基于损失厌恶的最优投资组合模型，研究不同风险资产的配置问题。

目前，大多数学者的研究都集中于损失厌恶系数和参照点保持不变的静态损失厌恶投资组合选择问题。现实中，投资者的损失厌恶程度和参照水平均会随着市场状态及投资者相对财富状况的变化而变化。因此，损失厌恶系数和参照点保持不变的假设并不完全符合投资者真实心理。

在Fortin等［12］的基础上，对动态效用函数进行改进，构建动态损失厌恶投资组合模型。为了反映不同市场状态下该模型的不同表现，以我国股票市场为背景，将其分为上升、下降和盘整三种状态，对比分析动态损失厌恶投资组合模型与损失厌恶系数和参照点不变的静态模型、M-V投资组合模型和CVaR投资组合模型的不同绩效表现，并对动态模型进行稳健性检验。

2 损失厌恶投资组合模型

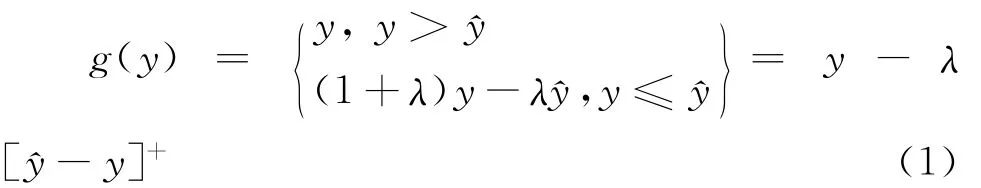
其中，λ≥0是损失厌恶系数，反映投资者的损失厌恶程度。y是投资组合收益率，^y∈R是给定的参照点，［a］+表示0和a中的较大值。从式（1）中可以看出，在参照点左右损失的斜率大于收益的斜率，说明投资者对损失比对收益更敏感。

损失厌恶投资组合模型考虑两种情形，一种是损失厌恶系数和参照点不变的静态损失厌恶情况，另一种是损失厌恶系数和参照点具有时变性的动态损失厌恶情况。

2.1 静态损失厌恶投资组合模型

静态损失厌恶投资组合模型是参照点和损失厌恶系数不变的损失厌恶投资组合模型。设整个投资期内有T个时期，x=（x1，…，xn）′，x为n种资产的权重向量，rt=（rt1，…，rtn）′，t=1，…，T，rt为第t期n种资产的收益率向量，第t期投资组合收益率yt=x，则由式（1）得，第t期损失厌恶效用函数为：

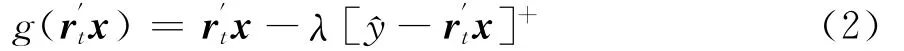
整个投资期预期损失厌恶效用最大化问题为：

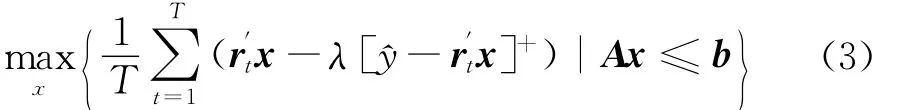
本文采用线性损失厌恶效用函数来研究损失厌恶投资者的最优资产配置行为，它是Kahneman和Tversky［1］提出的S-型损失厌恶效用函数的一种特殊情况，函数表达式为：

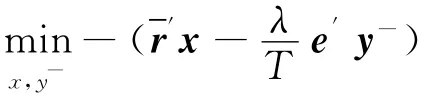
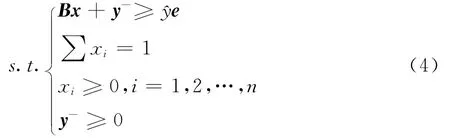
求解式（4）得静态损失厌恶投资组合模型的最优投资组合权重x*。

2.2 动态损失厌恶投资组合模型

动态损失厌恶投资组合模型是损失厌恶系数和参照点依赖于先前收益或损失而动态变化的损失厌恶投资组合模型。投资者在进行实际投资过程中，损失带来的负效用不仅取决于损失的大小还取决于该损失前期的投资表现。当投资者遭受损失时，如果在前期已经获得了收益，那么前期的收益会缓冲损失带来的负效用，如果其在前期也遭受了损失，投资者在经受损失之后，对额外的损失更加敏感等量的损失会带来更大的负效用。因此，在现实中应该考虑投资者的损失厌恶程度和参照点动态变化的情况，构建损失厌恶程度和参照点动态变化的投资组合模型。

采用Barberis［2］的动态变化规则调整损失厌恶系数和参照点：当投资者获得收益时，损失厌恶系数为初始λ值，参照点降低，低于无风险利率；当投资者遭受损失时，投资者损失厌恶系数增加，参照点等于无风险利率。动态变化的损失厌恶系数λt满足λt≥λ0≥0，λ0为初始损失厌恶系数；动态变化的参照点^yt满足0≤^yt≤r0t，r0t是第t期的无风险利率。

文献［12］中的动态损失厌恶效用函数为：

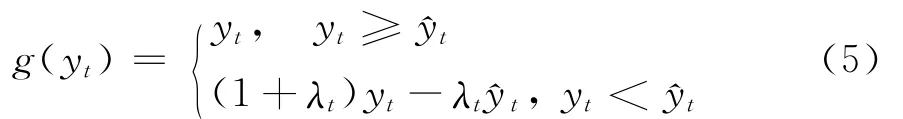
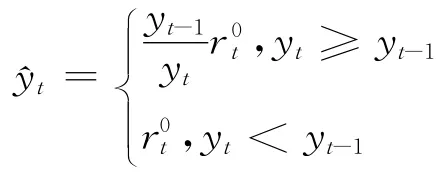
式（5）中存在两个问题：

（1）当yt＜0，yt-1＞0时，，则λt=λ0+，不满足动态变化中λt≥λ0≥0的要求。

（2）当yt-1＜0，yt＞0时，，则^yt=，不满足动态变化中的要求。因此，本文在构建动态损失厌恶投资组合模型时对文献［12］中的损失厌恶效用函数进行改进，将其收益率之间的比较换成资产组合价值之间的比较，解决了可能出现的λt＜λ0或^yt＜0的问题，改进的动态损失厌恶效用函数为

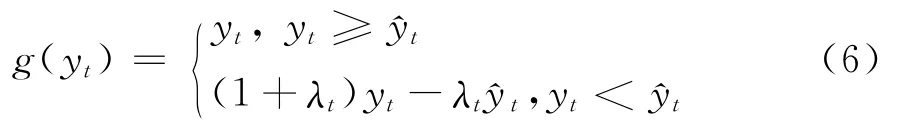
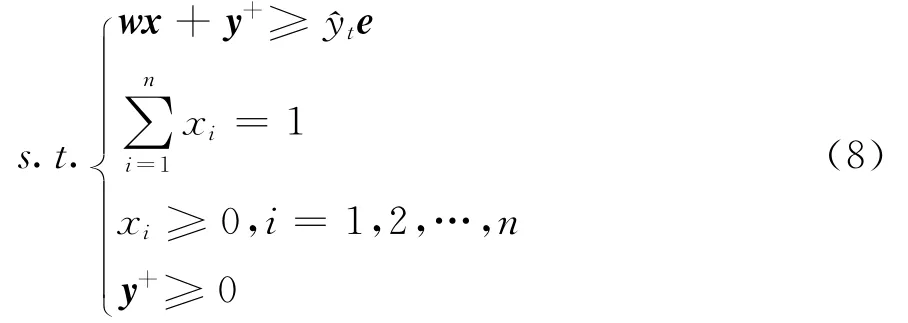
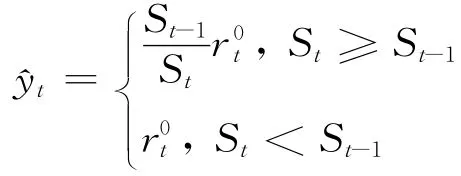
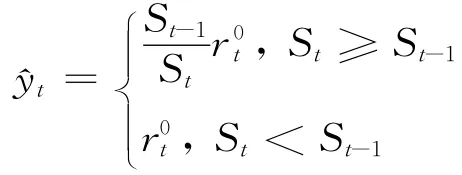
式（6）中，St为第t期投资组合价值，St-1为前期投资组合价值。用λt和^yt分别代替式（5）中的λ和^y，动态损失厌恶投资组合模型可以表示为。资产组合的期望净收益率为

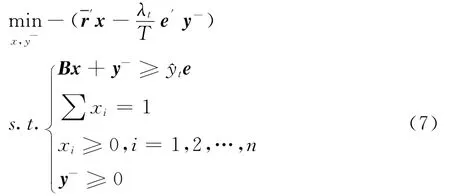
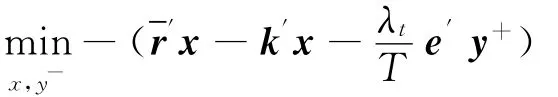
求解式（7）可得动态损失厌恶投资组合模型的最优投资组合权重x*。

2.3 具有交易成本的动态损失厌恶投资组合模型

在实际股市投资中，买入和卖出资产都会存在一定的交易成本，忽略交易成本可能会导致非有效的投资组合。因此，在损失厌恶投资组合模型中加入交易成本的因素来检验动态模型的稳健性。

假设买入和卖出第i种资产的交易成本是单位交易额的ki倍，k=［k1，k2，…，kn］′，k为单位成本向量。存在卖空限制xi≥0的条件下，交易成本函数为

3 实证分析

为研究动态损失厌恶投资组合模型的表现，计算各模型的最优投资组合权重、最优收益率和O-mega指数，并将动态损失厌恶投资组合模型与静态模型、M-V模型［16］和CVaR模型［17］的绩效进行对比。

3.1 数据选取

选用三种股票指数分别代表高、中、低风险资产构建投资组合，其中高风险资产为上证全指成长股，中风险资产为上证全指价值股，低风险资产为上证国债。用rt=pt/pt-1-1计算收益率，pt是第t个月的收盘价指数。选用的初始参照点为当期的活期存款利率。样本估计期间为2005年6月-2012年3月，数据来自Wind数据库。样本期间内，上证综合指数周收盘价具体走势如图1。

从图1可以看出，2005年6月-2007年10月为上升阶段，2007年11月-2008年10月为下降阶段，2008年11月-2012年3月为盘整阶段。各项资产的描述性统计见表1。

从表1可以看出，在整个样本期及上升和盘整阶段，成长股表现为高风险、高收益，价值股表现为中风险、中收益，国债表现为低风险和低收益。在下降阶段，国债收益率均值为8.23%，显著高于成长股和价值股，标准差为2.68%，显著低于成长股和价值股，因此，国债表现明显优于其他两种资产，在下降阶段应只投资于国债。基于以上分析，在实证部分主要研究四种模型在整体、上升和盘整三种情况下的最优资产配置和绩效表现。

3.2 计算过程与结果

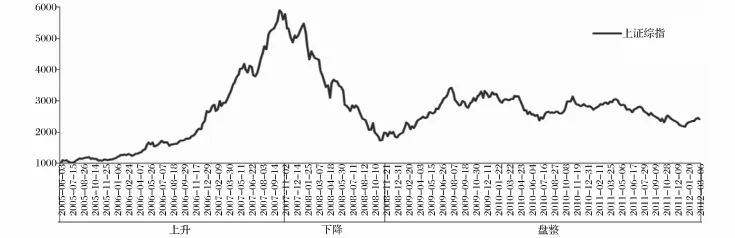
图1 2005年6月-2012年3月上证综指走势图

表1 各项资产的描述性统计（%）

表2 无交易成本各模型的资产比例构成（%）

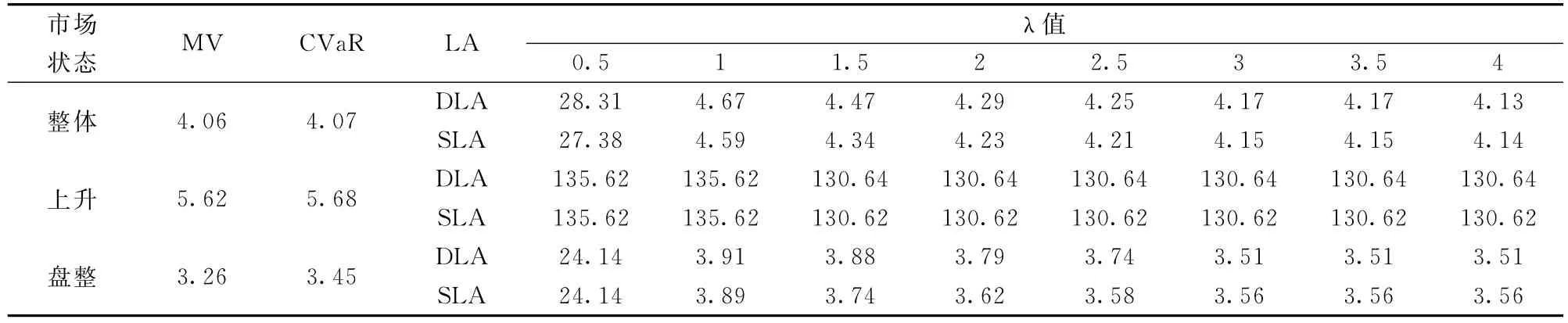
表3 无交易成本各模型的最优收益率（%）

第一步，计算最优投资组合权重。参考Kahneman和Tversky［18］通过实验得出的美国投资者损失厌恶系数中间值为2.25的结果，选择λ值区间为［0.5，4］，代表不同的初始损失厌恶程度。根据式（4）和式（7）利用MATLAB2010b，得到静态损失厌恶投资组合模型、动态损失厌恶组合模型及相同条件下的M-V模型、CVaR模型在三种情况下的最优投资组合权重x*，见表2。

第二步，计算最优投资组合收益率。按照所得最优权重和各资产在三种情况下的收益率均值，分别计算四种模型的最优投资组合收益率R*，见表3。

第三步，计算Omega指数值，得到Omega指数结果如图2-4。

图2 整体的Omega指数

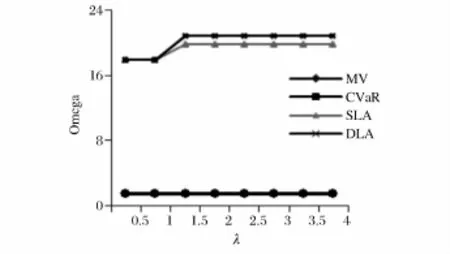
图3 上升阶段的Omega指数

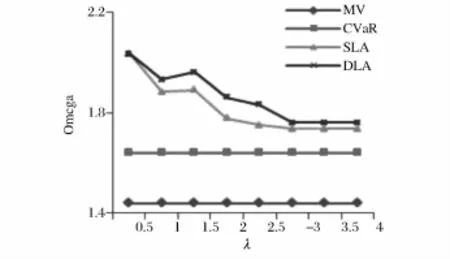
图4 盘整阶段的Omega指数

3.3 结果分析

3.3.1 最优权重结果分析

从表2可以看出，动态损失厌恶模型的最优资产配置比例分布特征为：（1）在整个投资期内，当λ =0.5，成长股权重为1，价值股和国债权重均为0。随着λ值逐渐增大，成长股权重逐渐减少，国债权重逐渐增加；（2）在上升阶段，当λ=0.5和1，成长股权重为1。当λ∈［1.5，4］，成长股和价值股的比例分别为59.48和40.52，国债的权重为0，此区间内λ值的变化对各资产比例无影响；（3）在盘整阶段，当λ=0.5，成长股权重为1。随着λ值逐渐增大，成长股权重逐渐减少，国债权重逐渐增加，价值股权重始终为0。

可以看出，在整个投资期内，损失厌恶投资者各资产分配相对分散，在高、中、低风险资产中均持有一定比例，投资者初始损失厌恶程度不同，各资产比例有所不同。而在上升阶段，投资者只投资于高、中风险资产，在盘整阶段，只投资于高、低风险资产。

3.3.2 Omega指数结果分析

（1）损失厌恶投资组合模型与M-V模型、CVaR模型的比较。从图2-4可以看出，损失厌恶投资组合模型的Omega值均明显高于M-V模型和CVaR模型的相应值。

（2）动态模型与静态模型的比较。①从图2可以看出，在整个投资期内，动态模型的Omega值高于静态模型的相应值。且两模型的Omega值均逐渐下降；②从图3可以看出，在上升阶段当λ=0.5和1，两模型的Omega值相等。当λ∈［1.5，4］，动态模型的Omega值高于静态模型的相应值，此区间内λ值变化对Omega指数无影响；③从图4可以看出，在盘整阶段，当λ=0.5，两模型的Omega值相等。当λ∈［1，4］，动态模型的Omega值高于静态模型的相应值。两模型的Omega指数随着λ值增大均经历一个先下降后小幅上升最后逐渐下降的过程。

总之，在综合考虑收益和下方风险时，动态模型的Omega指数值高于静态模型的相应值。因此，动态损失厌恶模型优于静态损失厌恶模型。

3.4 稳健性检验

对动态损失厌恶投资组合模型进行稳健性检验，检验在具有交易成本的情况下其是否仍然优于静态模型、M-V模型和CVaR模型。考虑目前我国股票市场上的印花税和佣金比例等，设买入和卖出资产的交易成本分别为0.3%，整个投资期内进行投资的交易成本之和为0.6%。首先，根据式（8），利用MATLAB2010b，分别得到有交易成本的动态损失厌恶投资组合模型与相同条件下的静态模型、M-V模型和CVaR模型的最优权重结果，见表4。其次，按照所得最优权重和各资产的平均收益率净值，分别计算四种模型的最优投资组合收益率，见表5。最后，计算Omega指数，如图5-7。

（1）最优权重的稳健性检验结果

从表4可以看出，在λ值变化区间内，三种情况下动态损失厌恶模型的各资产权重分布特征与无交易成本时相似。在整个样本期和盘整阶段，该模型中各资产权重对λ值的敏感性有所降低。在上升阶段，损失厌恶模型中成长股的权重有所升高，价值股的权重降低。

（2）Omega指数的稳健性检验结果

从图5-7可以看出，存在交易成本时，损失厌恶模型的Omega指数值均高于M-V模型、CVaR模型的相应值。同时，动态模型和静态模型的关系与无交易成本时二者的关系相似。

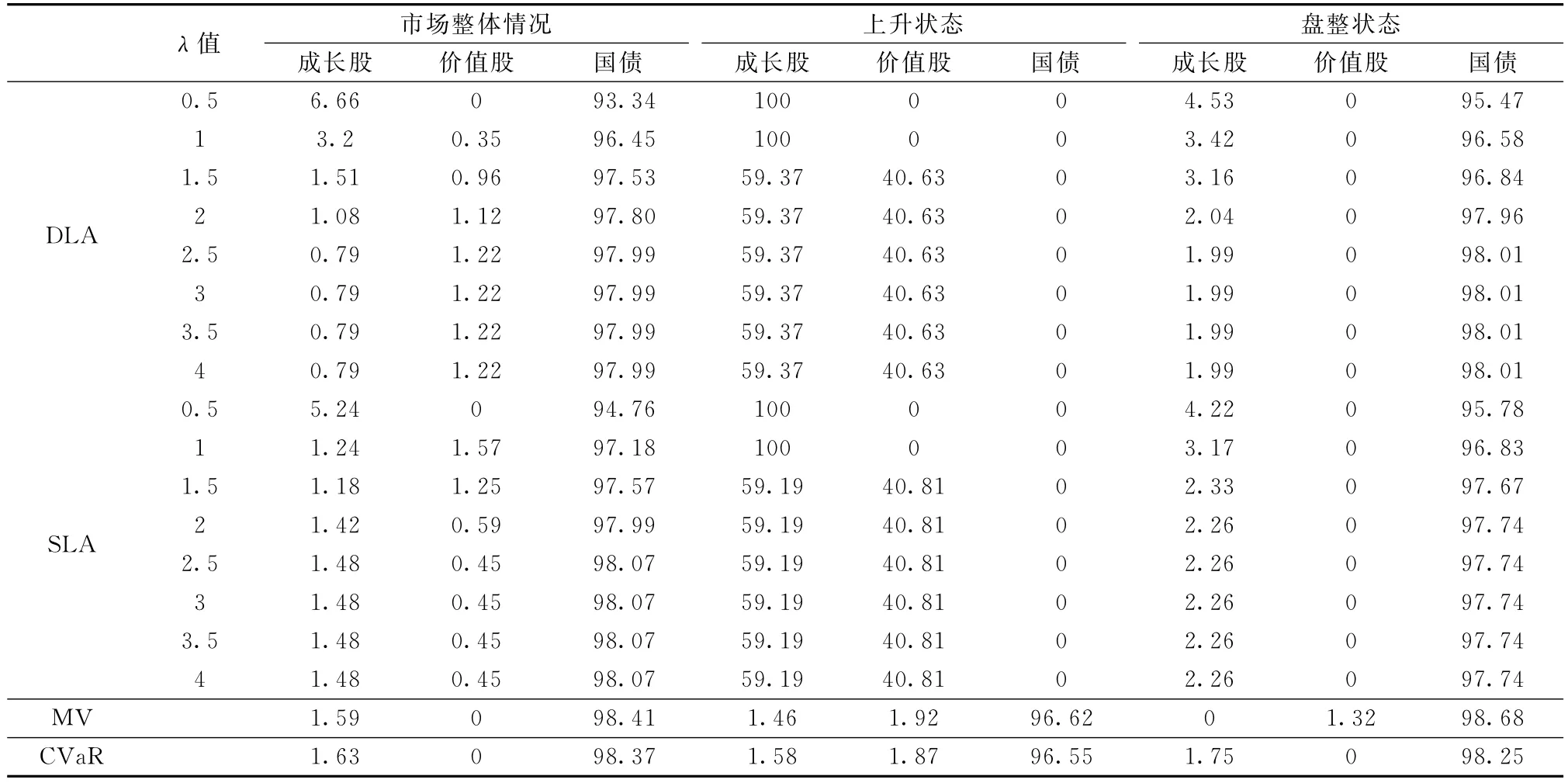
表4 有交易成本各模型的资产比例构成（%）

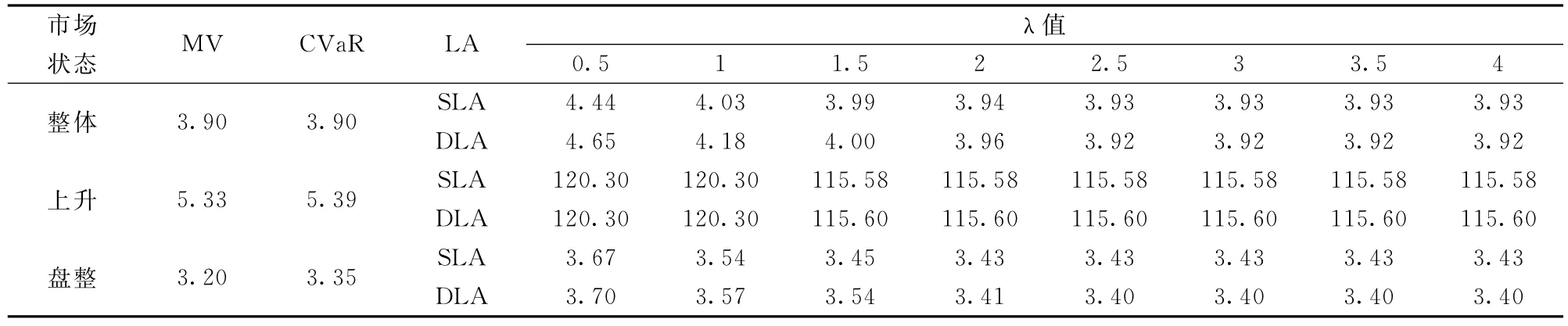
表5 有交易成本各模型的最优收益率（%）

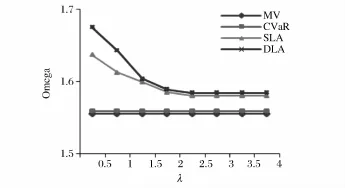
图5 整体的Omega指数

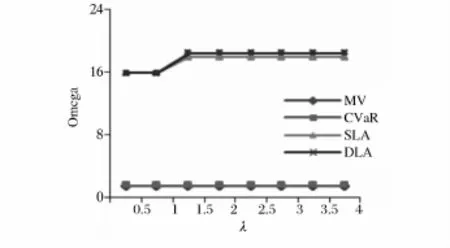
图6 上升阶段的Omega指数

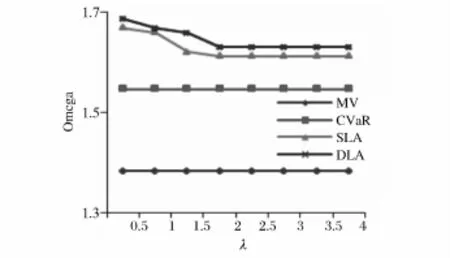
图7 盘整阶段的Omega指数

4 结语

建立动态损失厌恶投资组合模型，以我国股票市场为背景，探究在整个样本期及上升和盘整阶段动态损失厌恶投资组合模型的最优资产配置，

并将其绩效与静态模型、M-V投资组合模型和

CVaR投资组合模型进行比较。得出结论：（1）不同情况下，动态损失厌恶投资者具有不同的最优资产配置比例；（2）最优损失厌恶投资组合模型在

Omega指数方面均优于M-V和CVaR投资组合模型；（3）在整个样本期及上升和盘整阶段，动态损失厌恶投资组合模型在综合考虑收益和风险的

Omega指数方面优于静态模型。（4）在具有交易成本的条件下得出动态模型具有很好的稳健性。

以上结论表明投资者的损失厌恶和参照点动态变化的心理特征能够对其投资决策和投资行为产生一定影响。

［1］Kahneman D，Tversky A.Prospect theory：An analysis of decision under risk［J］.Econometrica，1979，47（2）：263-291.

［2］Barberis N，Huang Ming.Mental accounting，loss aversion，and individual stock returns［J］.Journal of Finance，2001，56（4）：1247-1292.

［3］Liberman N，Idson L C，Higgins E T.Predicting the intensity of losses vs.non-gains and non-losses vs. gains in judging fairness and value：A test of the loss aversion explanation［J］.Journal of Experimental Social Psychology，2005，41（5）：527-534.

［4］Gomes F J.Portfolio choice and trading volume with loss-averse investors［J］.Journal of Business，2005，78（2）：675-706.

［5］Zank H.On probabilities and loss aversion［J］.Theory and Decision，2010，68（3）：243-261.

［6］He Xuedong，Zhou Xunyu.Portfolio choice under cumulative prospect theory：An analytical treatment［J］. Management Science，2011，57（2）：315-331.

［7］Schmidt U，Zank H.What is loss aversion［J］.Journal of Risk and Uncertainty，2005，30（2）：157-167.

［8］Bernard C，Ghossoub M.Static portfolio choice under cumulative prospect theory［J］.Mathematics and Financial Economics，2010，2（4）：277-306.

［9］Berkelaar A B，Kouwenberg R，Post T.Optimal portfolio choice under loss aversion［J］.The Review of Economics and Statistics，2004，86（4）：973-987.

［10］De Giorgi E G，Legg S.Dynamic portfolio choice and asset pricing with narrow framing and probability weighting［J］.Journal of Economic Dynamics and Control，2012，36（7）：951-972.

［11］Blake D，Wright D，Zhang Yumeng.Target-driven investing：Optimal investment strategies in defined contribution pension plans under loss aversion［J］.Journal of Economic Dynamics&Control，2013，37（1）：195-209.

［12］Fortin I，Hlouskova J.Optimal asset allocation under linear loss aversion［J］.Journal of Banking and Finance，2011，35（11）：2974-2990.

［13］Fong W M.Time diversification under loss aversion：A bootstrap analysis［J］.Applied Economics，2013，45（5）：605-610.

［14］徐绪松，马莉莉，陈彦斌.考虑损失规避的期望效用投资组合模型［J］.中国管理科学，2007，22（5）：42-47.

［15］胡支军，叶丹.基于损失厌恶的非线性投资组合问题［J］.中国管理科学，2010，25（4）：28-33.

［16］Markowitz H.Portfolio selection［J］.The Journal of Finance，1952，7（1）：77-91.

［17］Anderson F，Mausser H，Rosen D.Credit risk optimization with conditional Value-at-Risk criterion［J］. Mathematical Programming，2000，89（2）：273-291.

［18］Kahneman D，Tversky A.Advances in prospect theory：Cumulative representation of uncertainty［J］.Journal of Risk and Uncertainty，1992，5（4）：297-323.

Optimal Asset Allocation Based on Dynamic Loss Aversion Portfolio Model and Empirical Research

JIN Xiu，WANG Jia，GAO Ying
（School of Business Administration，Northeastern University，Shenyang 110819，China）

Considering the psychological characteristics of loss aversion from the perspective of behavioral finance，a dynamic loss aversion portfolio optimization model that maximizes the expected utility is constructed.Dividing China's stock market into three states including rise，decline and consolidation，we empirically study the optimal asset allocation and performance of the dynamic loss aversion portfolio model is empirically studied comparing it with static loss aversion portfolio model as well as mean-variance and CVaR portfolio models.It is found under different market conditions，dynamic loss aversion investors have different optimal asset allocation ratios.Meanwhile，dynamic loss aversion portfolio model clearly outperforms static model，mean-variance portfolio model and CVaR portfolio model.The conclusions above can provide investors with advice when making investment decisions.

dynamic loss aversion；asset allocation；robust test；prospect theory

F830.91

：A

1003-207（2014）05-0016-08

2012-09-11；

2013-02-28

国家自然科学基金资助项目（70771023）

金秀（1963-），女（汉族），辽宁辽阳人，东北大学工商管理学院，教授，博士生导师，研究方向：金融工程.