On Existence of Local Solu tions of a M ovingBoundary Prob lem M odelling Chem otaxis in 1-D

WU Shaohua and YUEBo

SchoolofM athematicsand Statistics,Wuhan University,Wuhan 430072,China.

On Existence of Local Solu tions of a M oving
Boundary Prob lem M odelling Chem otaxis in 1-D

WU Shaohua and YUEBo∗

SchoolofM athematicsand Statistics,Wuhan University,Wuhan 430072,China.

Received 23Ap ril2014;Accep ted 31August2014

.w e p rove the local existence and uniqueness of am oving boundary p roblem m odeling chem otactic phenom ena.We also get the exp licit rep resentative for the m oving boundary in a special case.

Keller-Segelm odelof chem otaxis;m oving boundary;localexistence;special case.

1 In troduction

In thispaper,w eare in terested in am oving boundary p roblem due to a chem otaxism odel w hich w as introduced by Keller and Segel[1].Them odel readsas follow s

w here u(x,t)and v(x,t)stand respectively for the density of the considered species and that of the chem ical w hich triggers them ovem ent,constantsχ,γ,µandβare positive param eters,Ωis a bounded open subset in RN(N≥1)w ith sm ooth boundary∂Ω,and n is unit ou ter norm al vector of∂Ω.The p roblem(1.1)is intensively stud ied by m any

au thors and m ost resu lts have been devoted to the investigation of som e lim it cases correspond ing to particu lar choicesof the param etersχ,γ,µandβabove.Oneof them is that the d iffusive velocity ofγtends to infinity,w hich leads to the follow ing system(see[2])

w here R

Ωu0d x=|Ω|,|Ω|rep resents the volum e ofΩ.

For the p roblem(1.2),m any resu lts have been gained by som e authors(see for instance[2–6]).Since the spatial d iffusive velocity of v ism uch faster than that of u,it m akes sense that the spatial dom ain occupied by u is a subsetof the spatial dom ain occup ied by v at the sam e tim e.In otherw ords,letΩ⊂RNbe a bounded open dom ain andΩ0⊂⊂Ωbe an open sub-dom ain.Assum e a popu lation density u(x,0)occupying the dom ainΩ0,and in the ou tside ofΩ0the popu lation density u(x,0)≡0 and the external signal v occupyingΩ.For t＞0,u(x,t)sp reads to dom ainΩt⊂Ω,let∂Ωtdenote the boundary ofΩtand ntdenote the ou ter norm al vector of∂Ωt,thenΓt=∂Ωt×(0,T)is the m oving boundary.

The spatial d iffusion of species is referred to them oving boundary ofΩtw hich is occup ied by the specie at the tim e t≥0.Observe the flux is increasing w ith respect to the density of the species,so itw ou ld be reasonable to suppose that flux is p roportional to the density.Thusw e have follow ing flux cond ition on∂Ωt,

w here k(x,t)is a positive function,and 1/k(x,t)＞0 ism ass flow ratio. On the other hand,noticing that the fu ll flux on∂Ωtis

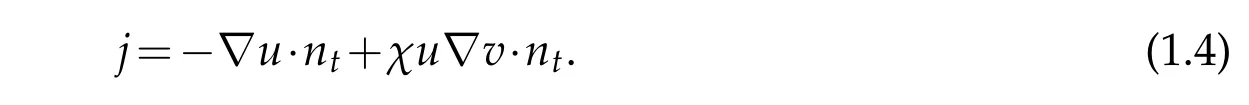
By conservation of popu lation,one has

w here vntis the norm ald iffusion velocity of∂Ωt. Assum eΓt:Φ(x,t)=0,then

Notice that

thus(1.6)and(1.7)give

We use(1.8)in(1.5)to obtain

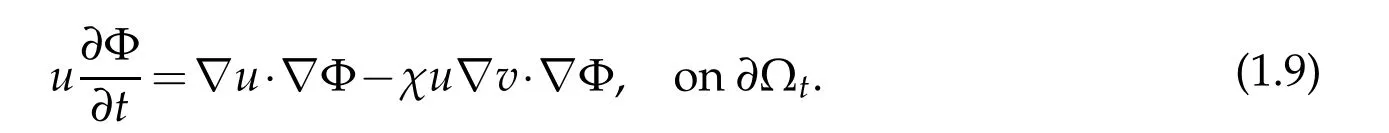
A t lastw e obtain the cond itionsof them oving boundaryΓt

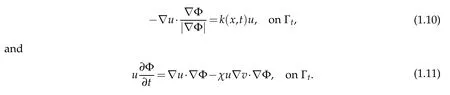
Therefore the fu llm oving boundary p roblem reads

w hereΓt:Φ(x,t)=0 is them oving boundary.

Rem ark 1.1.If N=1 andΓt:x-h(t)=0,then∇Φ=1 and∂Φ/∂t=-d h/d t,the cond itions of them oving boundary convert into

Rem ark 1.2.Under the case of Rem ark 1.1,if u＞0 onΓt,then(1.14)isequivalen t to

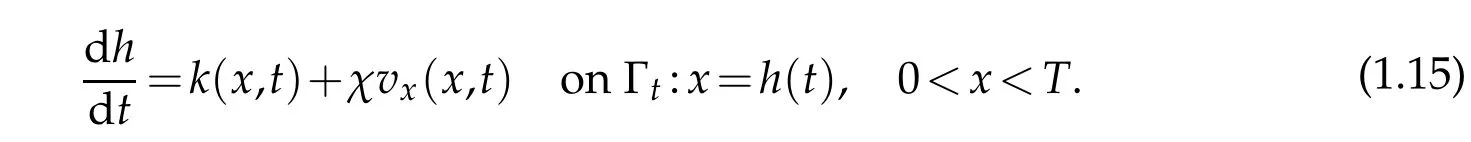
We consider one d im ensionalm oving boundary p roblem(1.12).W ithou t loss of generality,w e assum e thatΩ0=(0,b)w ith 0＜b＜1,Ω=(0,1),and for sim p licity,letχ=1.In this case,them oving boundary p roblem can be regarded as follow ing p roblem

w here u0＞0 and RΩ0u0d x=1.H.Chen and S.Wu(see[7])have given the localexistence and uniquenessof thism oving boundary p roblem(1.16)for the case k(x,t)≡k,w here k＞0 isa constant,gotten theexp licit rep resentative for them oving boundary,and show ed the finite-tim e blow up and chem otactic collapse for the solu tion of the p roblem.

In this paperw ew ou ld d iscuss the case of k(x,t)∈C([0,1]×[0,T0]),t0＜T0,w here T0is a given positive constan t.

2 M ain resu lts

Letus consider the follow ing system:

w here k(x,t)∈C([0,1]×[0,T0]),u0＞0 and RΩ0u0d x=1.Ou r app roach here is to find a rad ically symm etric solu tion for the p roblem(2.1)We need to find a pair(u,v)and a cu rveΓt:x=h(t),h(0)=b,to solve them oving boundary p roblem(2.1).

Now,for tw o positive constants M0andσ,satisfying M0＜m in{b,1-b}/(2t0),t0＜T0and 1＜σ＜2,w e define

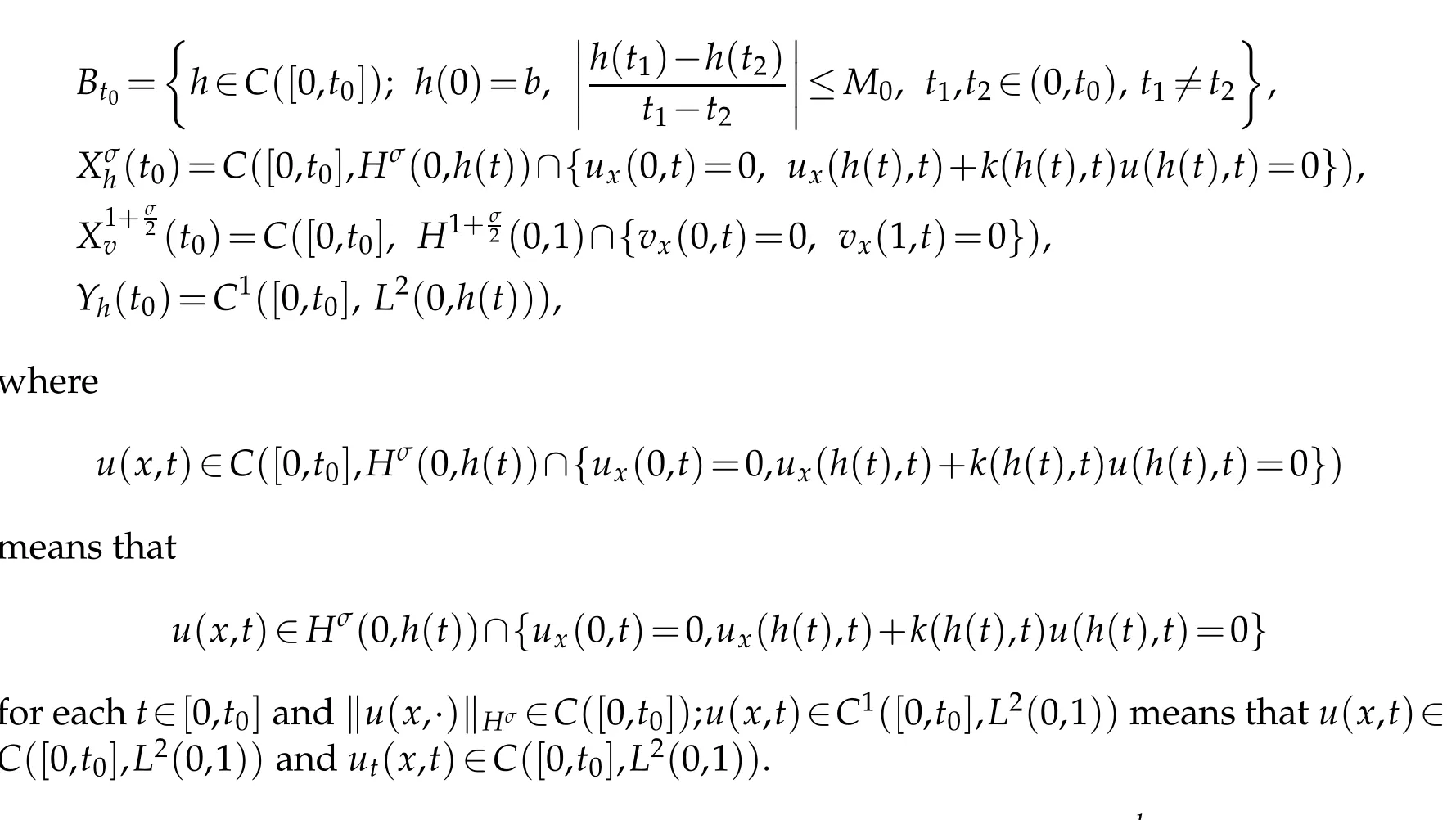
which are thesolutionsof(2.1)forsome t0＞0 smallenough.

3 Som e lemm as

and for each 1＜σ＜2 and t0smallenough

where C dependson M0but is independent oft0and h∈Bt0.

Proof.Take the transform

w here 0＜ξ＜1,0＜τ＜t0.

so the p roblem(3.7)has a unique solu tion

for each t0.

Thus

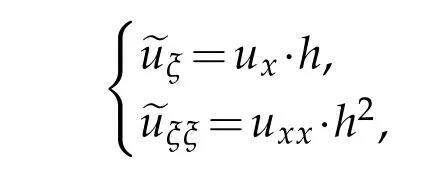
We know that Tt1(τ)isa holom orphic sem igroup on X and

Thus for f∈Hλ,one has

w here C is dependenton M0but independentof t1.

If t′＞0,then take t1=t′in(3.8),one has

In particu larw e have

By using the estim ate(3.9),one can deduce

w here C dependson M0bu t is independen tof t′and h∈Bt0.

Accord ing to(3.10)and(3.13)-(3.15),for t′sm allenough,it is obvious that

In case of t′=0,then for each 0≤t2≤t0,w e have

From(3.16)and(3.17)w e can easily obtain the estim ate(3.4),Lemm a 3.1 is p roved.

For the p roblem(3.2),ifωsatisfies that R10ω(ξ,t)dξ=1 for each t,then from a d irect calcu lation,one has

So w e know

4 Localexistenceand uniqueness form oving boundary p rob lem

In thissection,w e p rove theexistenceand uniqueness for the localsolution of them oving boundary p roblem(2.1).Ou rm ain resu lt is

In order to p rove this theorem,for each h(t)∈Bt0,w e first consider follow ing p roblem

Then from(3.18),(3.19)and Lemm a 3.2,w e know that for 0≤t1≤t2≤t0≤T0,

here

and c is independentof t0.Let M2denote the constan tat the righthand side of(4.4),if t0is sm allenough,then

Thusw e can choose M0=M2,thatm eans s(t)∈Bt0.Observe that Bt0⊂C[0,t0]isa com pact, closed and convex subset.

Define G:h(t)→s(t),then G m aps Bt0in to Bt0.We can p rove that G is a con tractive m app ing,then the fixed point theorem yields that there exist a pair(u,v)and a curve Γt:x=h(t)w hich are the solu tion of(4.1).

In fact,for h1(t),h2(t)∈Bt0,let(u1,v1)and(u2,v2)rep resent the correspond ing solutionsof(4.2)respectively.Then for 0≤t≤t0,one has

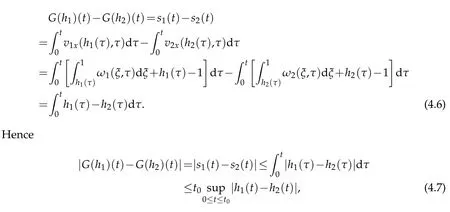
thatm eans them app ing G is contractive if 0＜t0＜1.Thusw e have p roved follow ing lemm a:

Next,w e can deduce that

Lemm a 4.2.Ifu0＞0,k u0kL1(0,b)=1and(u,v)is the solution ofthe system(4.1),then for t0＞0

smallenough,wehaveu＞0 and k u kL1(0,1)=k u0kL1(0,b)=1.

Proof.Since u0(x)＞0,by standard m axim alp rincip le of the parabolic equation,it follow s that u＞0.Integrating the firstequation of(4.1)over(0,h(t)),w e have

as required.

ProofofTheorem 4.1. Considerω∈C([0,t0],L∞(0,1)),satisfying Rh(t)0ω(x,t)d x=1,andω= 0,for h(t)＜x＜1,0＜t＜t0.Let u∈Xσh(t0)be the correspond ing solu tion of(4.1),w e define am ap G1by G1(ω)=u.

w here M=2C k u0kH2,and the constant C isgiven by theestim ate(3.4).Thus from Lemm a 4.1 and Lemm a 4.2,w e know that e BMis nonem p ty.

By using Lemm a 3.1 and Lemm a 3.2,w e have

Since the constan t C is independentof t0,so the estim ate above show s that

for t0＞0 sm allenough,w hichm eans that them app ing G1m apsin to

Forω1,ω2∈e BM,let u1,u2denote the correspond ing solution of(4.1)respectively.Set

Sim ilar to the p roof of Lemm a 3.1,one can obtain that for each 1＜σ＜2 and t0＞0 sm all enough

w here C dependson M bu t is independentof t0and h∈Bt0. On the other hand,w e have

w hich im p lies that them app ing G1is contractive for t0＞0 sm all enough.So it is p roved that,for a fixed h∈Bt0,the p roblem

Concerning the uniquenessof the solu tion,from the p rocessabove,w e know that the solution u is unique,but the solu tion v is notunique since if(u,v)is a pair of solution of (2.1)then for any constan t c,(u,v+c)is also a pair of solu tion of(2.1).

5 The exp licit rep resen tative of them oving boundary in a special case

Letus consider a special case that k(x,t)=µ(t)∈C[0,T0].Then a d irect calcu lation gives follow ing unique solu tion:

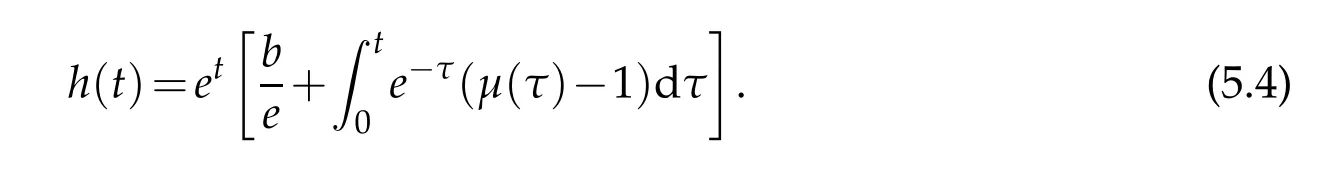
Thusw e have p roved follow ing resu lt:

[1]Keller E.F.,Segel L.A.,Initiation of slim em old aggregation view ed asan instability.J.Theor. Biol.,26(1970),399-415.

[2]Herrero M iguel A.,Vel´azquez Juan J.L.,Singu larity patterns in a chem otaxism odel.M ath. Ann.,306(1996),583-623.

[4]Nanjund iah V.,Chem otaxis signal relaying and aggregation m orphology.J.Theor.Biol.,42 (1973),63-105.

[5]Nagai T.,Blow-up of rad ially symm etric solu tions to a chem otaxis system.Adv.M ath.Sci. Appl.,5(1995),581-601.

[6]Child ress S.,Chem otactic collapse in tw o d im ensions,Lectu re Notes in Biom ath.Sp ringer-Verlag,55(1984),61-66.

[7]Chen H.,Wu S.,Them oving boundary p roblem in a chem otaxism odel.Comm.Pure Appl. Anal.,11(2012),735-746.

10.4208/jpde.v27.n3.7 Sep tem ber 2014

∗Correspond ing au thor.Emailaddresses:WUSH8@sina.com(S.Wu),yuebo060713@163.com(B.Yue)

AM SSub jectClassifications: 35A 01,35K57,35M 10,35L10,47D03,35R35

Chinese Lib rary Classifications: O175.28,O175.29