Quenching Tim e fora Sem ilinearHeatEquation w ith a Non linear Neum ann Boundary Cond ition

LIRuifei,ZHU Lip ingand ZHANG Zhengce,∗School ofM athematics and Statistics,Xi’an Jiaotong University,Xi’an 70049, China.

2College ofScience,Xi’an University ofArchitecture&Technology,Xi’an 710055, China.

Quenching Tim e fora Sem ilinearHeatEquation w ith a Non linear Neum ann Boundary Cond ition

LIRuifei1,ZHU Lip ing2and ZHANG Zhengce1,∗1School ofM athematics and Statistics,Xi’an Jiaotong University,Xi’an 710049, China.

2College ofScience,Xi’an University ofArchitecture&Technology,Xi’an 710055, China.

Received 19 January 2014;Accep ted 3M ay 2014

. Inthispaperweconsider thef initetimequenchingbehaviorofsolutionsto a sem ilinear heatequation w ith a nonlinear Neum ann boundary condition.Firstly,w e establish cond itions on nonlinear source and boundary to guarantee that the solution doesn’tquench for all tim e.Second ly,w e give su fficient conditions on data such that the solu tion quenches in finite tim e,and derive an upper bound of quenching tim e. Third ly,underm ore restrictive cond itions,w eobtain a low erbound ofquenching tim e. Finally,w e give the exactbounds of quenching tim e of a specialexam p le.

Nonl inearNeumannboundary;quenching;quenchingt ime.

1 In troduction

In this paper,w em ainly study the follow ing initial-boundary value p roblem

w hereνis the exterior norm al vector of the∂Ωassum ed sm ooth enough,Ωis a starshaped sm ooth ly bounded dom ain in(N≥2),and u0(x)is a positive bounded function satisfying the com patibility cond itions.We say a solution u of the p roblem(1.1) quenches in finite tim e,ifu＞0 exists in the classical senseforall t∈[0,T),and satisfies

Ifquenching occurs,w e denote the quenching tim e by T,or else T=∞.

Quenching p roblem s have been stud ied by m any researchers(see[1–8]and the references therein),since the initialw ork of Kaw arada[9]appeared in 1975.Contrary to quenching,another singu larity is called blow up,w e refer to[10–15]and the references therein for the latest resu ltsof blow up p roblem s.

In[16],Fila and Levine stud ied the quenching phenom enon of the equation

Hu and Yin[17]stud ied theblow up p rofilenear theblow up tim e for theheatequation

Recently,Payne etal.[18–20]stud ied the blow up phenom ena and derived the upper and low er bounds of blow up tim e of Eq.(1.1)under certain assum p tions of f and g. As w e know,m any au thors considered the rate estim ates of the blow up or quenching solu tions,and even blow up tim e estim ate,bu t very few ones stud ied the exact estim ate ofquenching tim e.In thispaper,under the d ifferentassum p tionsof f and g,w e consider the quenching p roblem,and study the estim ate of quenching tim e.First,w e show the criteria for the solution u of(1.1)non-quenching and get the upper and low er boundsof quenching tim eof p roblem(1.1).M oreover,w egivean exam p le to show theapp licability ofour resu lts.In the paper,w e shalluse the follow ing Sobolev type inequality

2 Criteria for non-quenching

Throughout this paper,w e use k and c to denote various generic constants if there is no con fusion.

Theorem2.1.Assume that functions fand g satisfy thefollow ing conditions

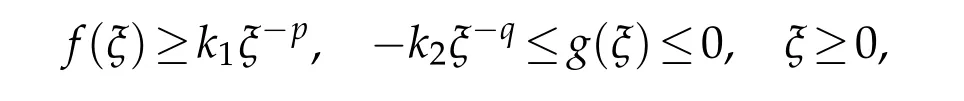
w ith nonnegative constants k1,k2.M oreover,assume that p,q＞1,and p-1＞2q.Then the solution u of(1.1)w illnot quench forall time.

Proof.Defineφ(t)=RΩu-2d x.Differentiating and using the assum p tions abou t f and g, w e obtain

w herew e use the equality∇(u-n)=-nu-(n+1)∇u.SinceΩis the star-shaped dom ain, and

In tegrating it,so w e have the follow ing inequality(see[19,Lemm a A.1])

So w e can rew riteφ(t)into

Using arithm etic-geom etricm ean inequality,w e have

w ithσ=(3+q)d1k2/(6ρ1).It follow s from(2.4)and(2.5)that

w ithα=(p-1-2q)/(p-q)and arbitraryε＞0.Note thatα∈(0,1)in view of p-1＞2q w ith p,q＞1.By inserting(2.7)in(2.6),w e obtain

w here|Ω|is the N-volum e ofΩ.So

so w e can rew rite(2.8)in to

Remark2.1.Clearly,w hen f,g are both nonnegative functions,quenching w ill never occu r,w hereas itw illdo if f,g are both negative.Herew e adm itand om it the details.

3 Criteria for quenching

Theorem3.1.Letu(x,t)be the classical solution oftheproblem(1.1),and assume thefollow ing conditions on the data

where0≤β≤α,f,g≤0,f′,g′≥0,f′,g′≤0,andΔu0≤0.M oreover,weassumeΨ(0)＞0w ith

Proof.By them axim um p rincip le,w e know that ut≤0.Define

Using the hypotheses stated in this theorem,w e obtain

sinceΨ(t)＞0,w hich will be p roved.M oreover,from the definition ofΨ(t),w e obtain

Togetherw ith(3.4),w e get

Clearly,thisinequalitycannotholdsforalltime.Infact,thisinequalityleadsto

NowweproveΨ′(t)≥R2aRΩ(ut)2dxR＞0,infactfromtheinequality(3.6)and2-2a＞0,we onlytoneedtoproveΩ(ut)2dx+Ω∇u·∇utdx≥0. ApplyingGreen’stheorem,wederive

Letv,Δu,thenvsatisfiestheproblem

Remark 3.1.In this theorem,Ω needs not to bestar-shaped domain.

4 Lower bound for quenching time

In this section, we will seek the lower bound for the quenching time T if quenching occurs,andassumethatΩ⊂is a bounded star-shaped domain and convex in two orthogonal directions.Before the proof,we defineχ(t)=RΩu-2ndx.

Theorem4.1.Letu(x,t)betheclassicalsolutionoftheproblem(1.1)inΩ.Assumemoreover that

ifp＜n-1,where c1,c2,c3are nonnegative constants.For p＞n-1,the solution u w ill not quench forall time.

Proof.From the definition ofχ(t),w e obtain

w herew e use the equality∇(u-n)=-n∇u·u-(n+1).SinceΩis star-shaped dom ain,and

Integrating itand app lying the Divergence’s theorem,so

w here d,d1,ρ0,ρ1are defined in(2.3)(see[19,Lemm a A.1]).So w e can rew rite(4.3)in to

w hereµis a nonnegative constant,w hich w ill be determ ined.Nextw e use the Sobolev type inequality(see[20,Eq.(2.10)])

valid for bounded star-shaped dom ainΩinassum ed to be convex in tw o orthogonal d irections and for arbitraryλ＞0.Com bining above inequalities,w e obtain

Forµ＞0 sm allenough,w e can chooseλ＞0 such that c5=0.This leads to

w here c1,c2,c3,c4are defined in(4.10).

In the particu lar case p=n-1,the d ifferentialequality(4.11)reduces to

If p＜n-1,since the follow ing inequality

This leads to the d ifferential inequality

If p＞n-1,w e are in the situation of Theorem 2.1.So w e com p lete the p roof of low er bound ofquenching tim e.

Rem ark 4.1.Through a sim p le calcu lation,if f(u)satisfies(4.1)for k1＞0,then ifquenching occu rs itw illbe ata tim e later than thatw hen f(u)=0.

Rem ark 4.2.W hen f,g and u0satisfy certain assum p tions,the solu tion u of the p roblem (1.1)m ay blow up(see[21,22]).In this paper,w e on ly consider the situationΔu0,f≤0, w hich can ensu re blow up w illnotoccu r before quenching.

5 An exam p le

In thissection,w ew illd iscuss the specialcase f(u)=0,g(u)=-u-q(q＞1).M oreover,w e derive the exactupper and low er boundsofquenching tim e of solution u of the p roblem

(1.1).Before the p roof,w e assum e thatΩsatisfies the hypothesisof Theorem 4.1.

Theorem 5.1.AssumeΔu0≤0,Ψ(0)＞0.Let g(u)=-u-q(q＞1),f=0,then thesolution u of problem(1.1)quenches in finite time T,and T satisfies

w ith nonnegative constants c1,c2,c3,whereΨ,Φandχare defined as in Theorems 3.1 and 4.1 respectively.

So H(t)≤H(0)-γt,w hichm eans that u quenching in finite tim e T.

Second ly,w e give the upper bound of quenching tim e.Since

valid for∀α≥0,β≥(3-q)/(q-1),then w e can chooseαsuch that 0≤β≤α.If q≥3,w e haveβ≥0;if q＜3,w e haveβ≥(3-q)/(q-1)＞0.So w e have by Theorem 3.1 that

Now w e give the low er bound of quenching tim e.Since k1=0,app ly Theorem 4.1, w e have

w here c1,c2,c3are defined in(4.10).So

Thusw e com p lete the p roof.

Acknow ledgm en ts

The au thorsw ou ld like to thank the refereesverym uch for their valuable comm entsand suggestions.

This w ork w as supported in part by the National Natural Science Foundation of China(No.11371286),the Scientific Research Foundation for the Returned OverseasChinese Scholars,State Education M inistry,the You th Foundation of NSFC(No.11401458), the Special Fund of Education Departm ent(No.2013JK0586)and the Youth Natu ral Science Grant(No.2013JQ1015)of ShaanxiProvince of China.

[1]Chan C.Y.,New Resu lts in Quenching,In:Proc.1stWorld Congressof Nonlinear Analysis, Berlin:Walterde Gruyter,1996.

[2]Deng K.,Xu M.,Quenching for a non linear d iffusion equation w ith a singu lar boundary cond ition.Z.Angew.M ath.Phys.50(1999),574-584.

[3]Deng K.,Xu M.,On solutions of a singu lar d iffusion equation.Nonlinear Anal.TMA.41 (2000),489-500.

[4]Gidas B.,Sp ruck J.,A p riori bounds for positive solutions of nonlinear ellip tic equations. Comm.PartialD ifferential Equations8(1981),883-901.

[5]Levine H.A.,Advance in Quenching.In:Proc Internet Con f on Reaction-Diffusion Equa

tions and Their Equilibrium States,Boston:Birkh¨auser,1992.

[6]Levine H.A.,Lieberm an G.M.,Quenching of solu tions of parabolic equationsw ith non linear boundary cond itions in severald im ensions.J.Reine Angew M ath.345(1983),23-38.

[7]Zhao C.L.,Blow-up and Quenching for Solutionsof Som e Parabolic Equations,Ph.D.thesis, Univ.of Louisiana,Lafayette,2000.

[8]Zhang Z.C.,LiY.Y.,Quenching rate for the porousm ed ium equation w ith a singu larboundary cond ition.Appl.M ath.9(2011),1134-1139.

[9]Kaw arada H.,On solutionsof initialboundary value p roblem for ut=uxx+1/(1-u).RIMS Kyoto Univ.10(1975),729-736.

[10]Zhang Z.C.,Gradientblow up rate for a viscous Ham ilton-Jacobiequation w ith degenerate d iffusion.Arch.M ath.4(2013),361-367.

[11]Zhang Z.C.,Hu B.,Grad ient blow up rate for a sem ilinear parabolic equation.Discrete Contin.Dyn.Sys.A26(2010),767-779.

[12]Zhang Z.C.,Hu B.,Rate estim atesofgradientblow up for a heatequation w ith exponential nonlinearity.Nonlinear,Anal.TMA.12(2010),4594-4601.

[13]Zhang Z.C.,LiY.,Blow up and existenceofglobalsolu tions to non linear parabolic equations w ith degenerate d iffusion.Electron.J.Differential Equations264(2013),17pp.

[14]Zhang Z.C.,Li Y.Y.,Grad ient blow up solu tions of a sem ilinear parabolic equation w ith exponentialsource.Comm.PureAppl.Anal.12(2013),269-280.

[15]Zhang Z.C.,Wang B.,Blow up rate estim ate for degenerate parabolic equation w ith nonlinear grad ient term.Appl.M ath.M ech.6(2010),787-796.

[16]Fila M.,Levine H.A.,Quenching on the boundary.Nonlinear Anal.TMA.21(1993),795-802.

[17]Hu B.,Yin H.M.,The p rofile near blow up tim e for solu tions of the heat equation w ith a nonlinear boundary condition.Trans.Amer.M ath.Soc.346(1994),117-135.

[18]Payne L.E.,Philippin G.A.and Piro S.Vernier,Blow-up pheonom ena for a sem ilinear heat equation w ith nonlinear boundary cond ition.I,Z.Angew.M ath.Phys.61(2010),999-1007.

[19]Payne L.E.,Philipp in G.A.and Piro S.Vernier,Blow-up pheonom ena for a sem ilinear heat equation w ith non linear boundary cond ition.II,Nonlinear Anal.TMA.73(2010),971-978.

[20]Payne L.E.,Schaefer P.W.,Bounds for the blow up tim e for the heatequation under non linear boundary cond itions.Proc.Royal Soc.Edinburgh 139A(2009),1289-1296.

[21]Deng K.,Zhao C.L.,Quenching versus blow-up.J.Partial Differential Equations 13(2000), 243-252.

[22]Deng K.,Zhao C.L.,Blow-up versus quenching.Commun.Appl.Anal.7(2003),87-100.

10.4208/jpde.v27.n3.3 Sep tem ber 2014

∗Correspond ing author.Email addresses:l i rui fei@stu.xj tu.edu.cn(R.Li),nyzhul iping@gmai l.com(L. Zhu),zhangzc@mai l.xj tu.edu.cn(Z.Zhang)

AMSSubjectClassifications:35A01,35B40,35K05,35K55

ChineseLibraryClassifications:O175.26