Strong Solu tions for Nonhom ogeneousIncom p ressib le Viscous Heat-Conductive Fluidsw ith Non-New tonian Poten tial

MENG Qiuand YUAN HongjunInstituteofM athematicsand Statistics,Beihua University,Jilin 132013,China.

2InstituteofM athematics,Jilin University,Changchun 130012,China.

Strong Solu tions for Nonhom ogeneous
Incom p ressib le Viscous Heat-Conductive Fluidsw ith Non-New tonian Poten tial

MENG Qiu1,∗and YUAN Hongjun21InstituteofM athematicsand Statistics,Beihua University,Jilin 132013,China.

2InstituteofM athematics,Jilin University,Changchun 130012,China.

Received 18 February 2014;Accep ted 13August2014Abstract.We consider the Navier-Stokes system w ith non-New tonian potential for heat-conducting incom p ressible fluids in a dom ainΩ⊂R3.The viscosity,heatconduction coefficients and specific heatat constant volum e are allow ed to depend sm ooth ly on the density and tem peratu re.We p rove the existence of unique local strong solutions forall initialdata satisfying a naturalcom patibility condition.The difficu ltof this typem odel ism ainly that theequationsare coup led w ith ellip tic,parabolicand hyperbolic,and the vacuum of density cause also m uch trouble,that is,the initial density need notbe positive and m ay vanish in an open set.

AM SSub jectClassifications:35A 05,35D35,76A 05,76D03

Chinese Lib rary Classifications:O 175.29

Strong solutions;heat-conductive fluids;vacuum;Poincar´e type inequality;non-New tonian potential.

1 In troduction

The governing system of equations for a heat-conducting viscous fluids under the selfgravitational forceand outer pow er can be described by them odelof the fluids dynam ic, that is,the incom p ressible fu ll Navier-Stokesequationsw ith non-New tonian poten tial:

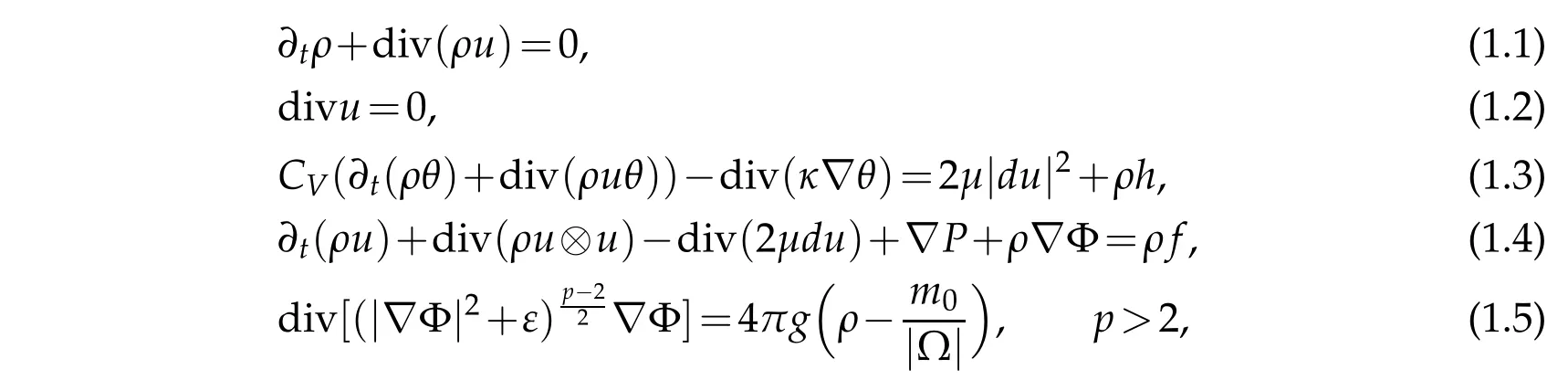
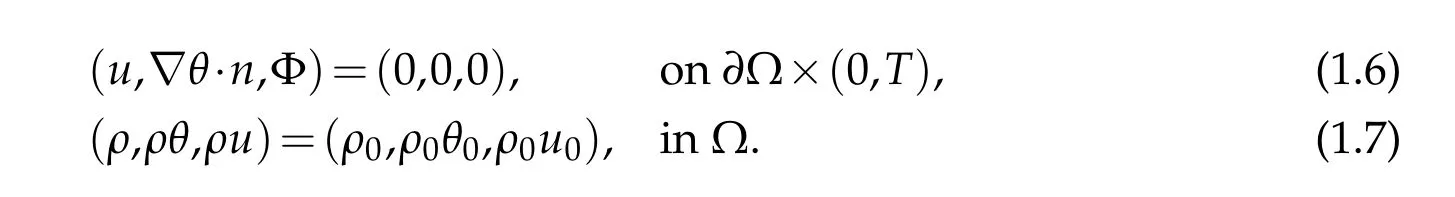
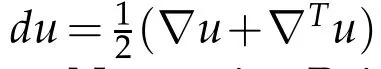
ForΦ=0,the p roblem has been stud ied by m any au thors[1–8].Very recen tly,Cho and Kim[9]show ed that the p roblem hasa unique localsolu tion(ρ,u,P,θ)w ith them ain hypothesis

and som e natu ral com patibility cond itions:

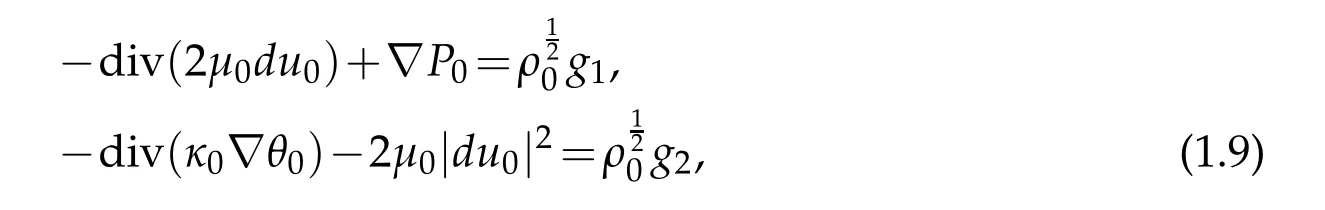
for som e P0∈H1(Ω)and functions(g1,g2)∈L2(Ω).And fu rther they assum e an add itional cond ition,such that

for nonconstant coefficients.

The aim of this paper is to use them ethod of[9]to p rove the existence of unique localstrong solu tions to(1.1)-(1.7)w ith infρ0=0.Here it shou ld be noted that,in[9],the au thorsp rescribed thehom ogeneousDirich letboundary cond ition for the tem peratu reθ, i.e.θ|∂Ω=0,instead of thehom ogeneousNeum ann boundary cond ition,i.e.∇θ·n|∂Ω=0, for technical reasons,w e w ill use a Poincar´e type inequality[10,11]to circum ven t this d ifficu lty.

The follow ing isou r MA IN RESULT.

Theorem 1.1.Assume that thedata(ρ0,u0,θ0,h,f)satisfy the regu larity condition

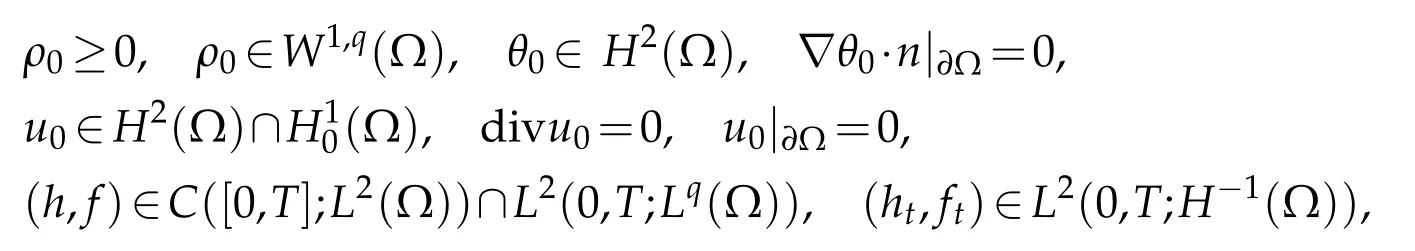
for some 3＜q≤6.Further assume the compatibility condition(1.9)and coefficient condition (1.10).Then there exists a small time T∗＞0 and a unique strong solution(ρ,u,θ,P,Φ)to the initialboundary valueproblem(1.1)-(1.7)such that

The detailed p roof of Theorem 1.1 is given in the follow ing tw o sections.In Section 2,w e consider a linearized p roblem and derive som e local estim ates for the solutions independent of the low er bound of the initial density and in Section 3,w e p rove the theorem by app lying classical iteration argum entbased on the uniform estim ates.

2 A p rioriestim ates for a linearized p rob lem

In this section,w e consider the follow ing linearized p roblem:

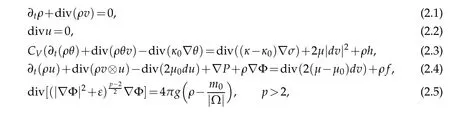
in(0,T)×Ωtogetherw ith the boundary and the initial cond itions

w herew ew rite

for sim p licity,throughou t this section,w e assum e that the data(ρ0,u0,θ0)satisfy cond ition

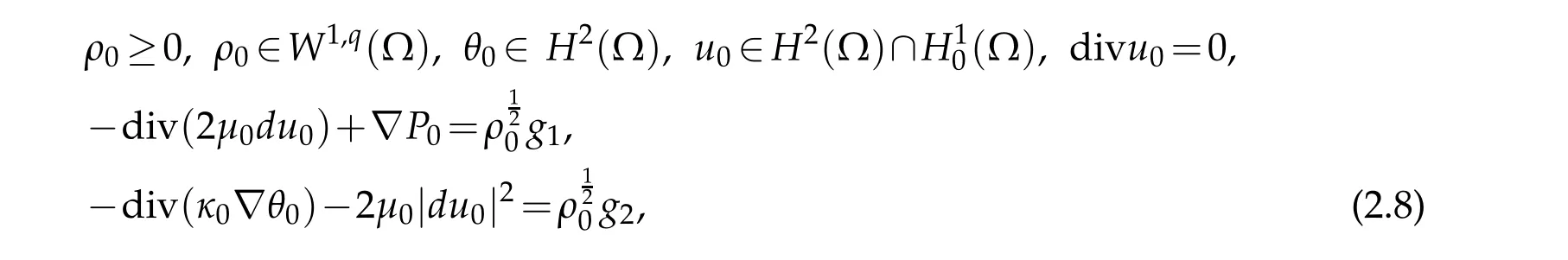
for som e q∈(3,6],P0∈H1(Ω)and(g1,g2)∈L2(Ω).We assum e fu rther that the pair(v,σ) of know n vector and scalar fields satisfies

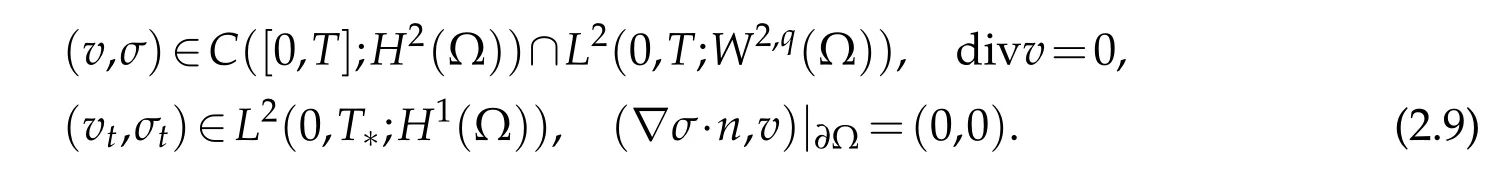
First,w e p rove an existence resu lt for the p roblem(2.1)-(2.7)for the case w hereρ0is bounded below aw ay from zero.

Lemm a 2.1.In addition to(2.8)-(2.9),weassume thatρ0≥δinΩforsome constantδ＞0.Then there existsa uniquesolution(ρ,u,θ,P,Φ)to the linearized problem(2.1)-(2.7)such that

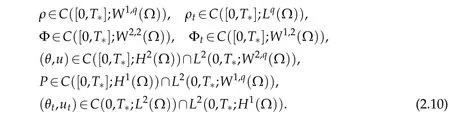
andρ≥δ/2 in(0,T∗)×Ω.

Proof.Since the p roof is the sam e as that in[9],w e om it the details here.

The purpose of this section is to derive som e local(in tim e)a p riori estim ates for (ρ,u,θ,P,Φ)w hich are independen t of the low er boundδofρ0.For this pu rpose,w e choose a fixed constant c0＞1 such that

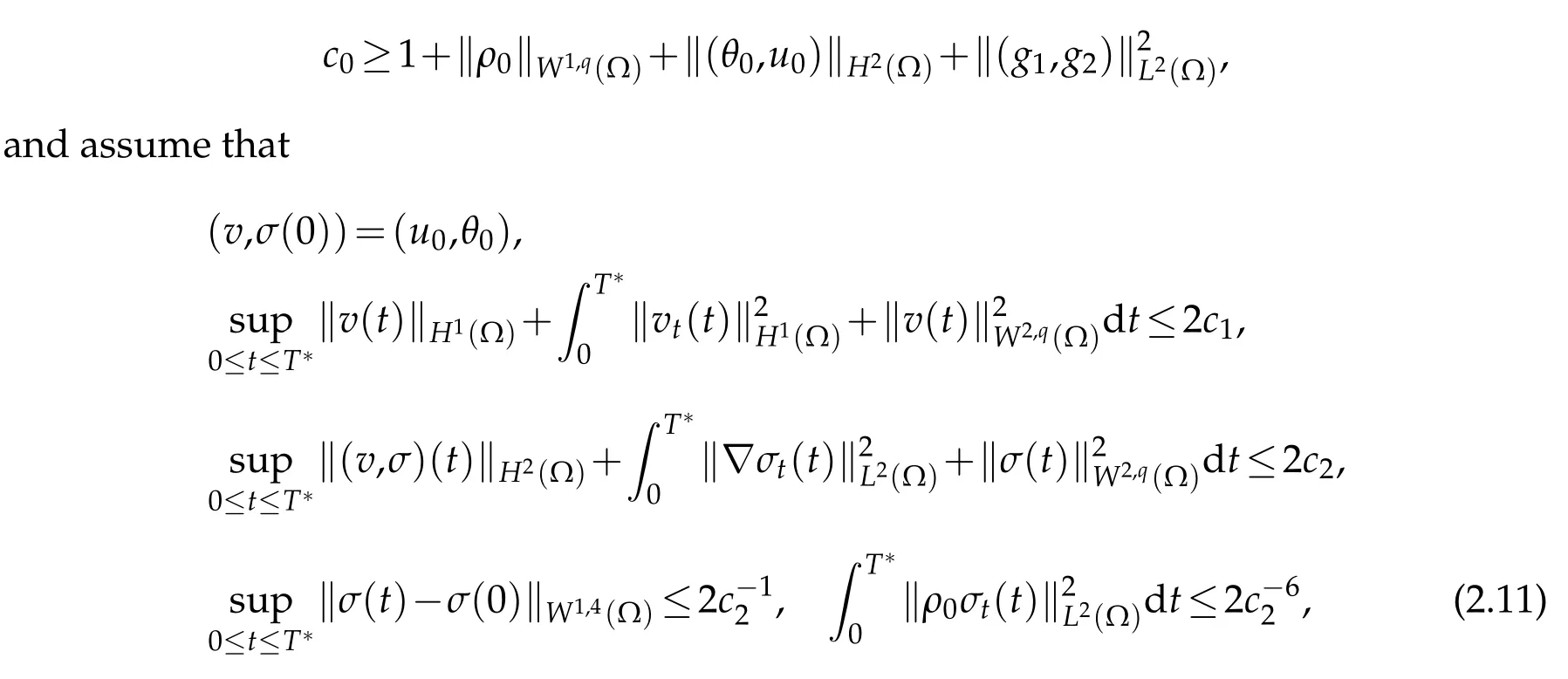
for som e constants c1,c2(independent ofδ),and T∗w ith 1＜c0≤c1≤c2and 0＜T∗≤T, w hich w illbe determ ined laterand depend only on c0and the param etersof C.Throughou t thisand the follow ing sections,w e denoteby C a generic positive constantdepend ing

on ly on the fixed constants q,T,kµkC1(R2),k CVkC1(R2)and kκkC1(R2).M oreover,M=M(·) denotes a generic increasing continuous function from[1,∞)to[1,∞)w hich depends on ly on the param etersof C,w ealso adop t the sim p lified notationµ(t)=µ(ρ(t),ρ(t)σ(t)), etc.

In[9],the au thors p roved the follow ing estim ates for the densityρ.

Lemm a 2.2.

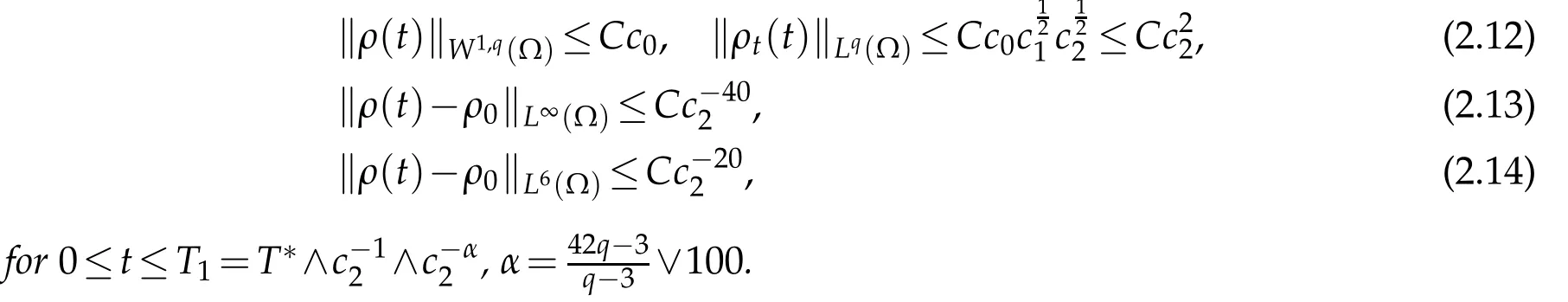
Here and later on w ew illuse a∧b=m in(a,b)and a∨b=m ax(a,b). Using(2.11)-(2.13),w e easily show that

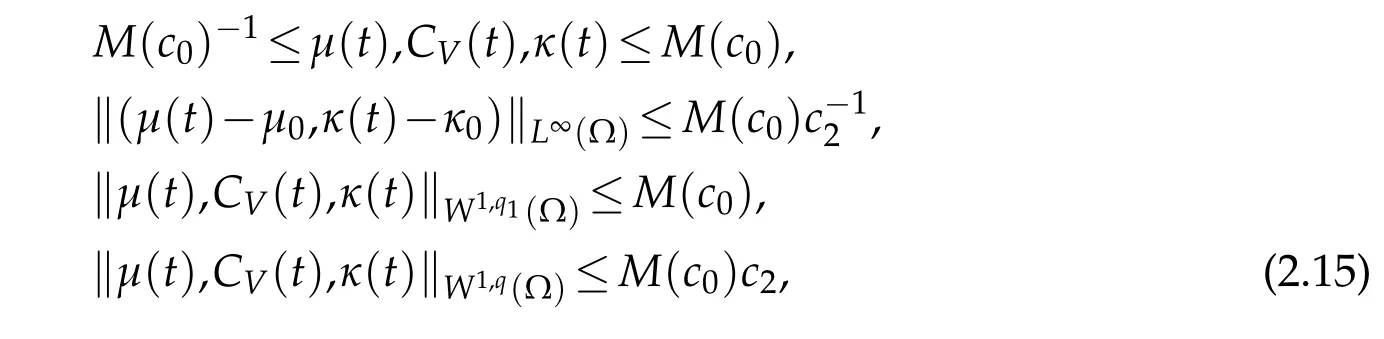
for 0≤t≤T1,q1=q∧4.M oreover,in view of(2.12)and(2.14),and using the Poincartype inequality[10,11]

Rem ark 2.1.The constant in(2.16)m ay depend onΩ,and thusw e do not know n how to solve the p roblem in an exterior dom ain w ith the hom ogeneous Neum ann boundary cond ition for the tem perature.

The next lemm a gives the estim ate on the non-New tonian gravitational potential.

Lemm a 2.3.Assume thatρ0≥δ＞0 inΩ.Then there exists a unique strong solutionΦto the initialboundary valueproblem(2.5)-(2.7)such that

Proof.M u ltip lying(2.5)byΦand integrating overΩ,w e get,

Next,d ifferentiating(2.5)w ith respect to tim e,m u ltip lying itbyΦtand integrating overΩ,w e get

Finally,letusestim ate k∇Φ(t)kH1(Ω),w e consider Eq.(2.5),

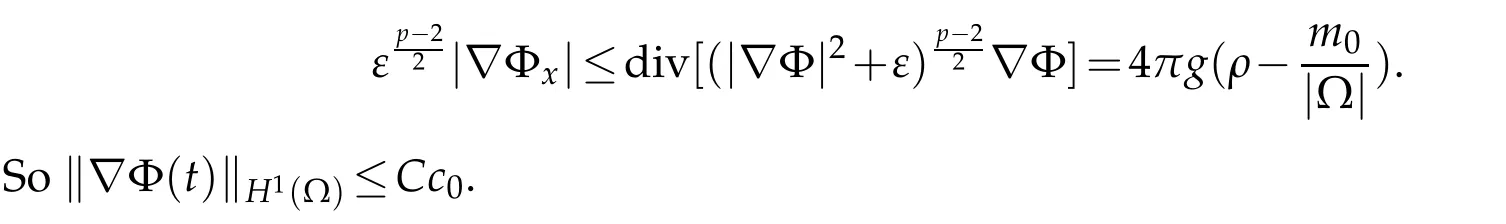
The next lemm a gives the estim ate on the velocity u,the calcu lations are very sim ilar to those in[9,14],w ew illom it the detailed p roofhere.

Lemm a 2.4.

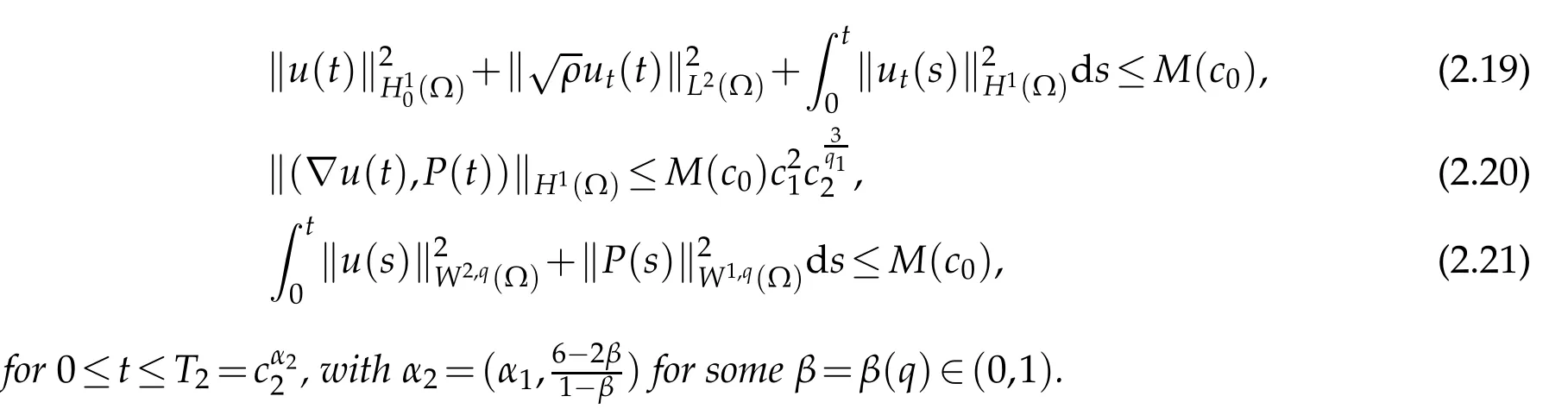
The next lemm a gives the estim ates on the tem peratu reθ,since w e consider the hom ogeneous Neum ann boundary cond ition forθ,w hich cou ld notbe dealw ith in[9],so w e detail the p roofshere.

Lemm a 2.5.

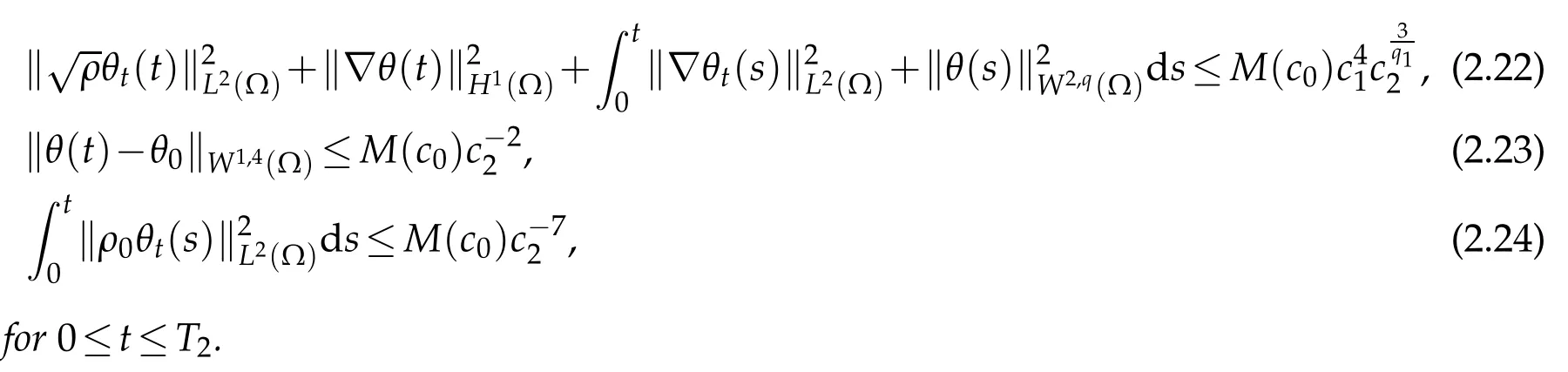
Proof.Differentiating(2.3)w ith respect to tim e,w e obtain

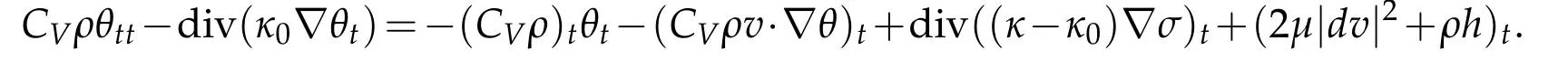
Thenm u ltip lying this byθtand integrating overΩ,w e have

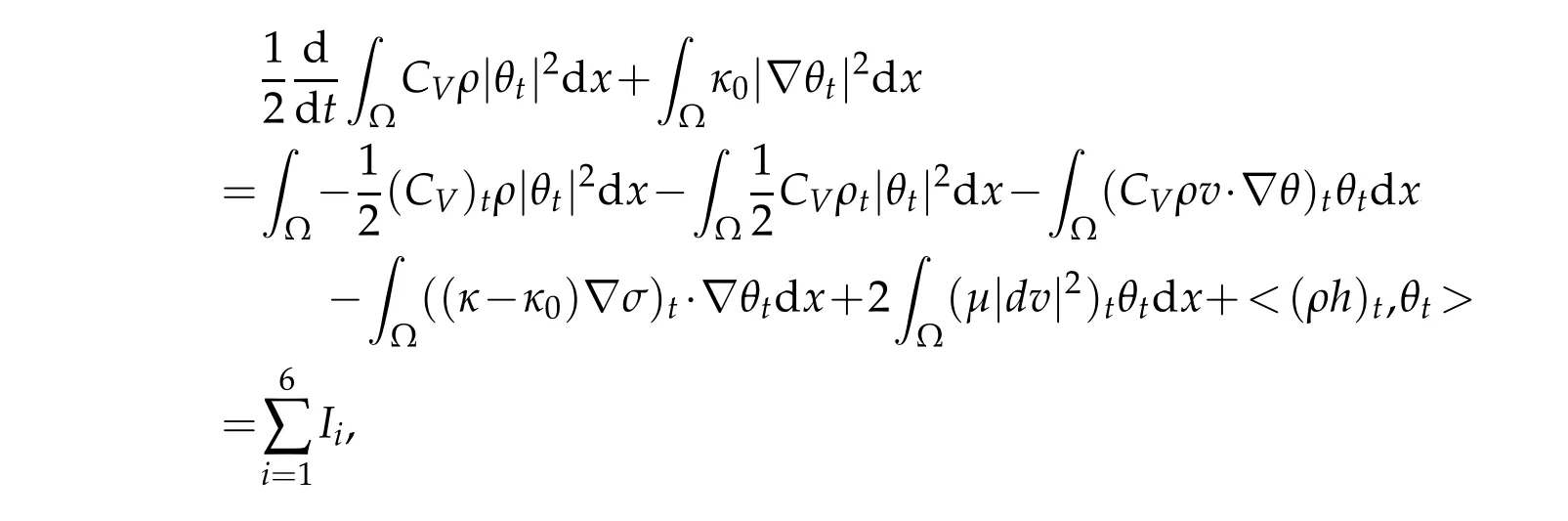
We use(2.12),(2.15),(2.17),(2.19)-(2.21)and the Poincar´e type inequality

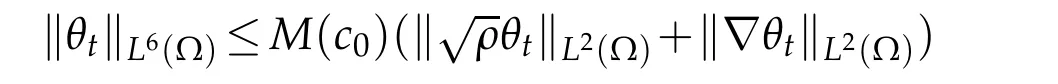
in[10,11]to bound Ii,1≤i≤6 as follow s:

Now using the interpolation inequality

The restof the calcu lations are the sam e as those in[9],w hich com p letes the p roof of the lemm a.

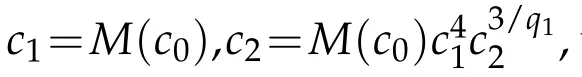
conclude that

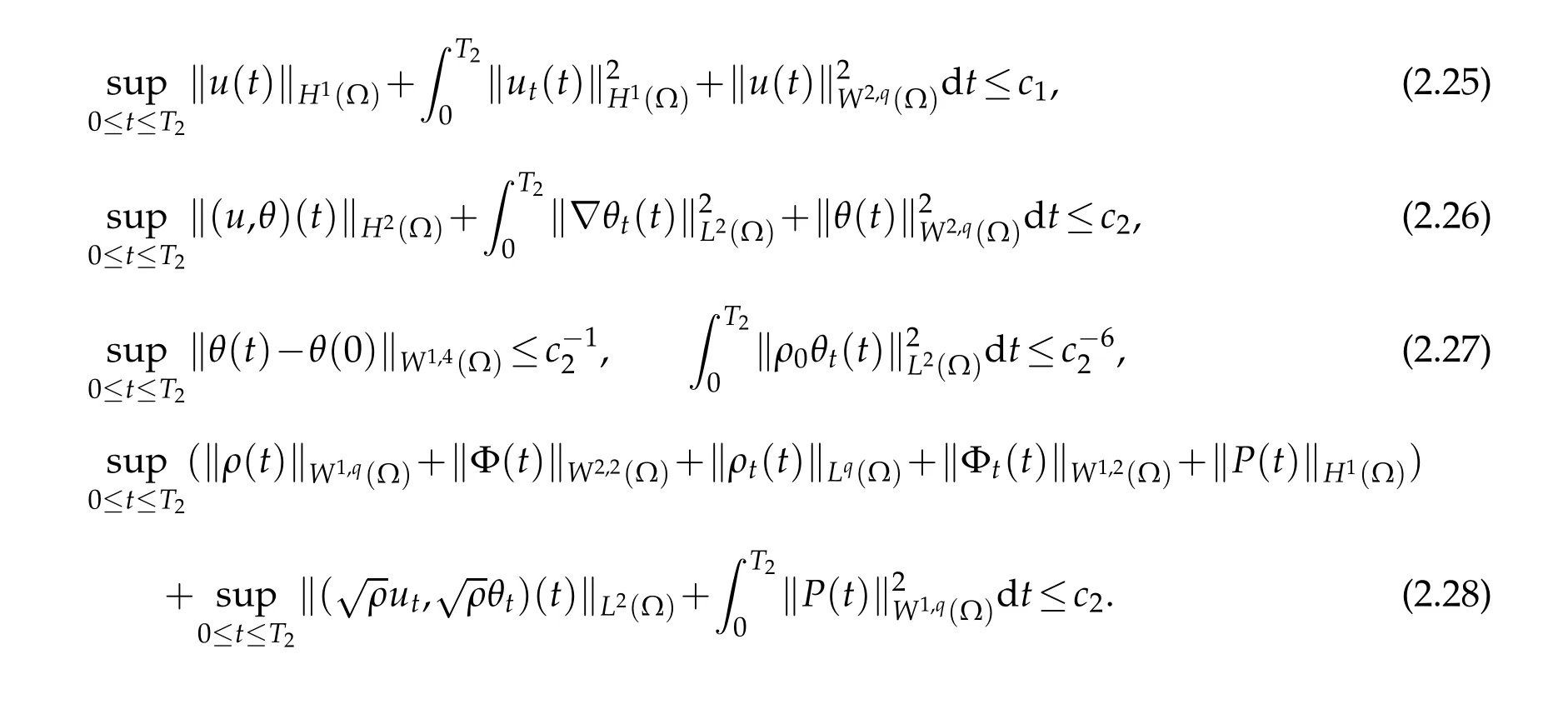
Now w e are in a position to p rove them ain resu lt in this section.

Lemm a 2.6.Assume that(v,σ)satisfies(2.9)w ith T replaced by T∗,and

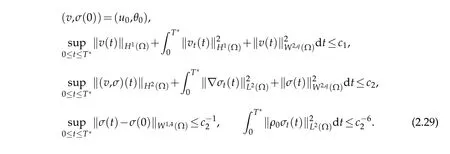
Then there exists a unique strong solution(ρ,θ,u,P,Φ)to the linearized problems(2.1)-(2.8)in [0,T∗]satisfying theestimates(2.25)-(2.28)aswellas theregularity

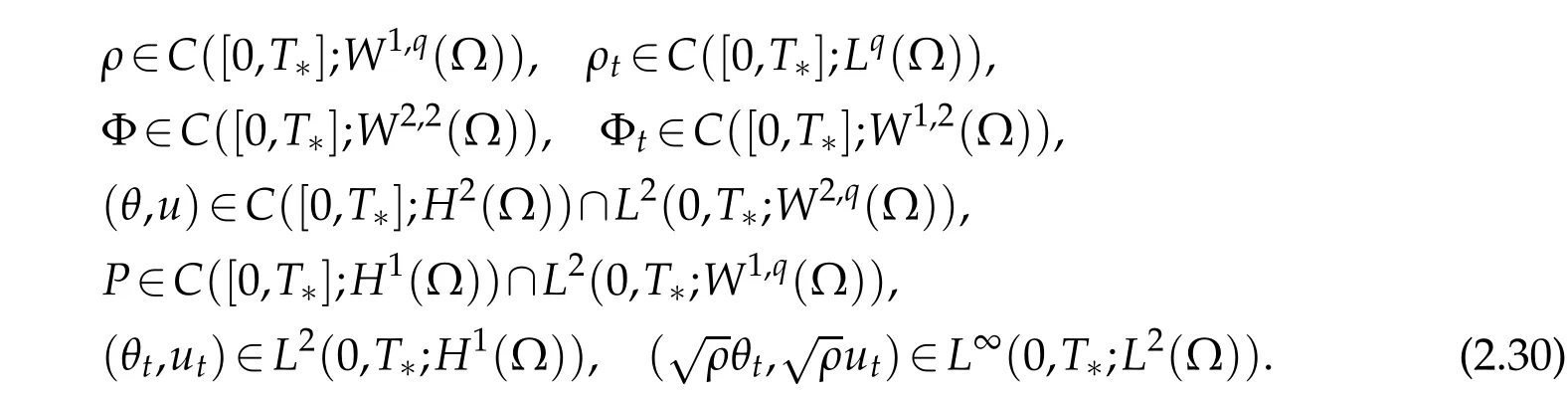
Proof.Since the p roofsare the sam e as those[9],w e om it the detailshere.

3 Proof of Theorem 1.1

Our p roofw illbe based on theusual iteration argum entand on the resu lts(in particu lar, Lemm a 2.6)in the last section.

Let u0,θ0∈C([0,∞);H2(Ω))∩L2(0,∞;H3(Ω))be theunique solutions to the follow ing linear parabolic p roblem s,respectively.

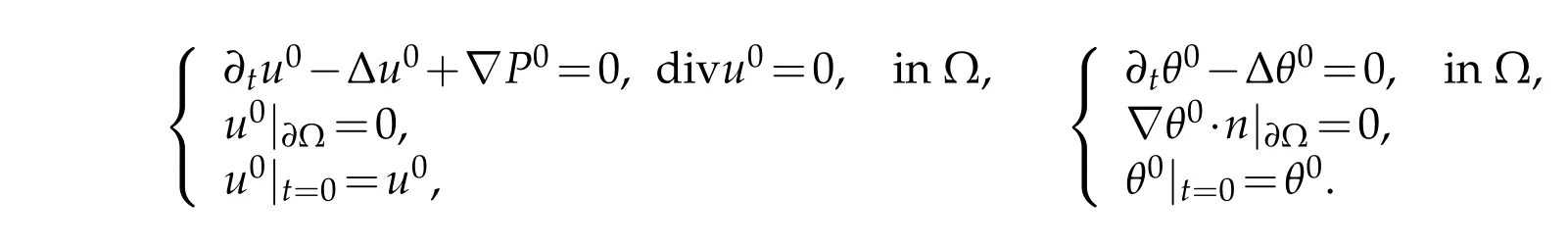
Then using the sam e p roofs as in[9],it is easy to p rove that

M oreover,sinceθ0∈C([0,∞);H2(Ω)),θ0t∈L2(0,∞;H1(Ω))andρ0∈L3(Ω),there isa sm all tim e T∗∈(0,1)such that

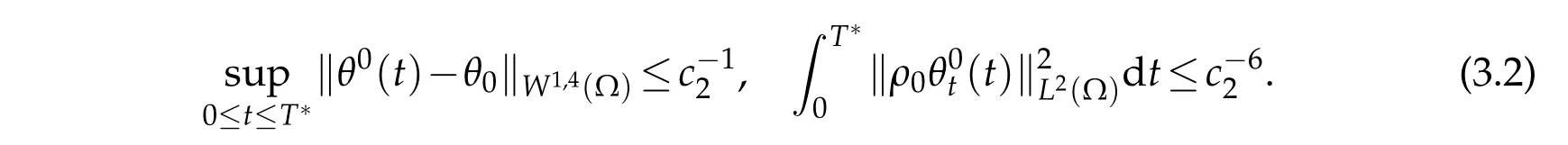
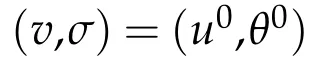
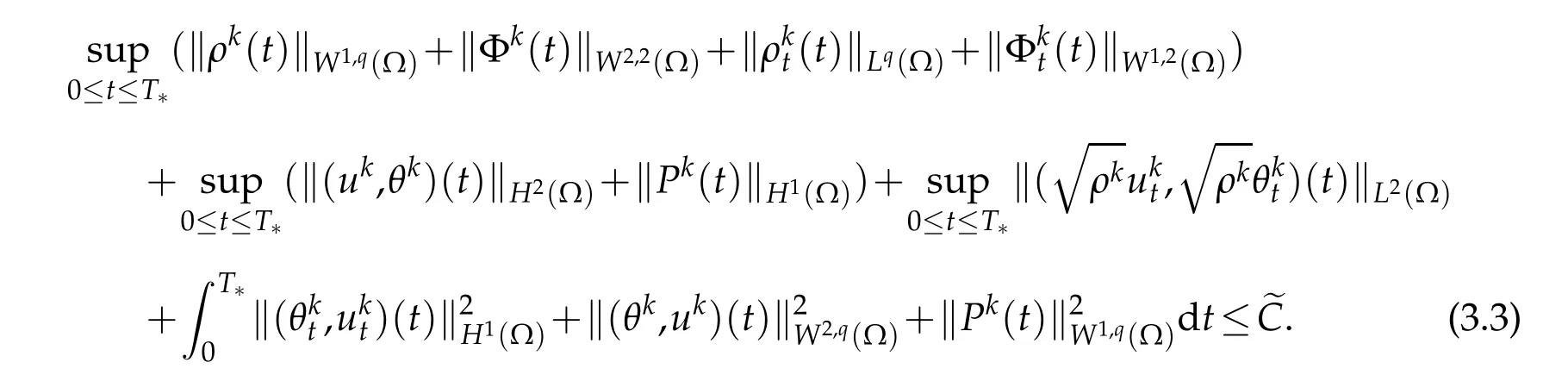
Throughout the p roof,w e denote by e C a generic constant depend ing on ly on c0and the param eters of the constan t C,bu t independen tof k.

From now on,w e show that the fu llsequence(ρk,uk,θk,Pk,Φk)converges to a solution to the originalnonlinear p roblem(1.1)-(1.7)in a strong sense.

Letus define

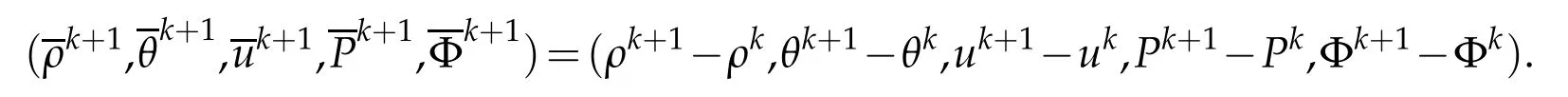
Then from(2.1)-(2.5),w e derive the equations for the d ifferences

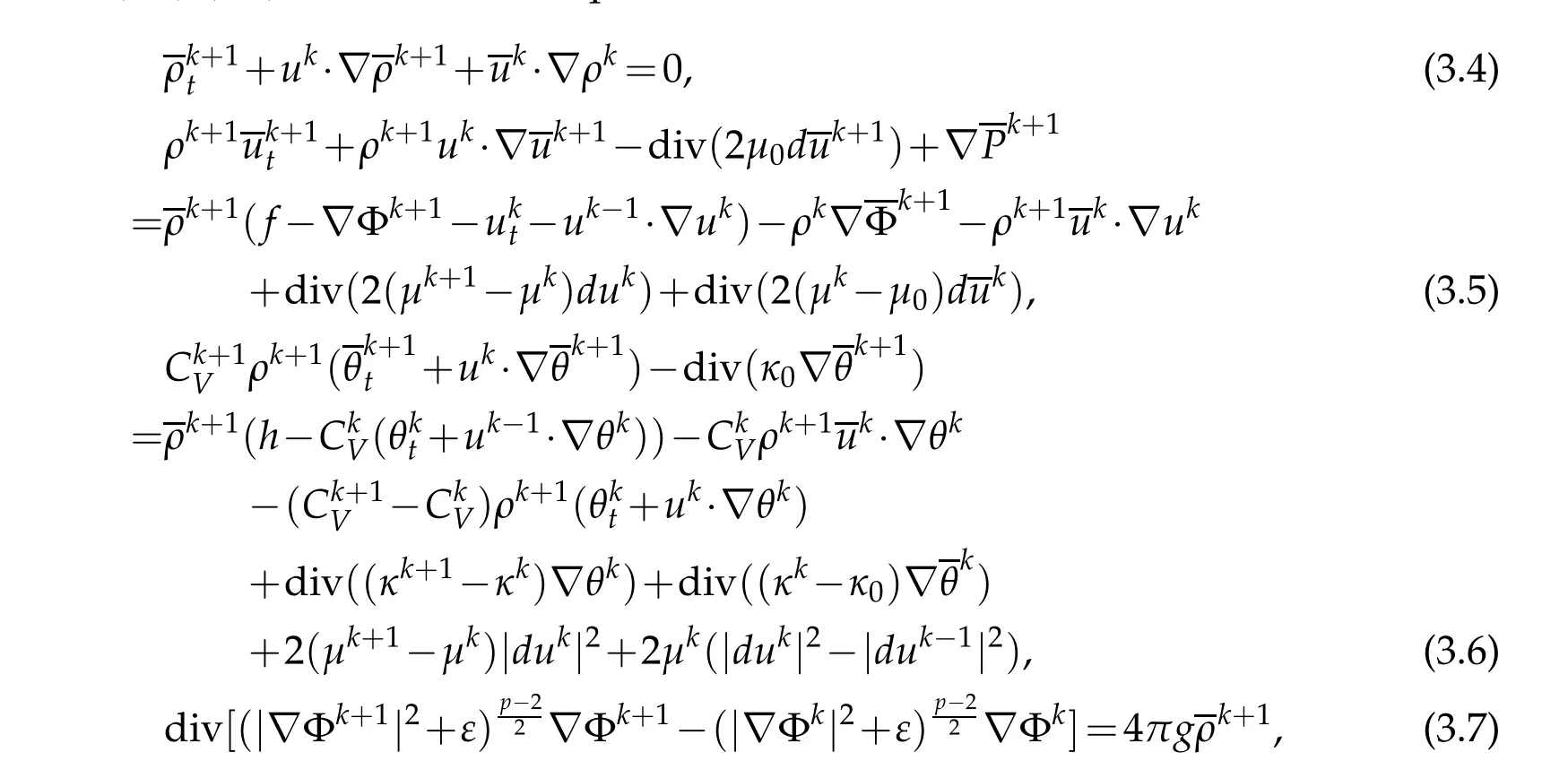
w hereµk+1=µ(ρk+1,ρk+1θk),etc.

First,m u ltip lying(3.4)byρk+1and in tegrating overΩ,w e obtain

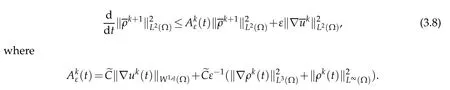
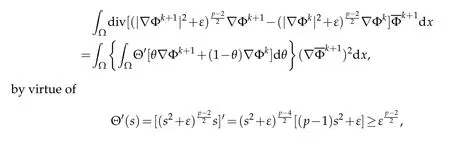
Thus,w e have

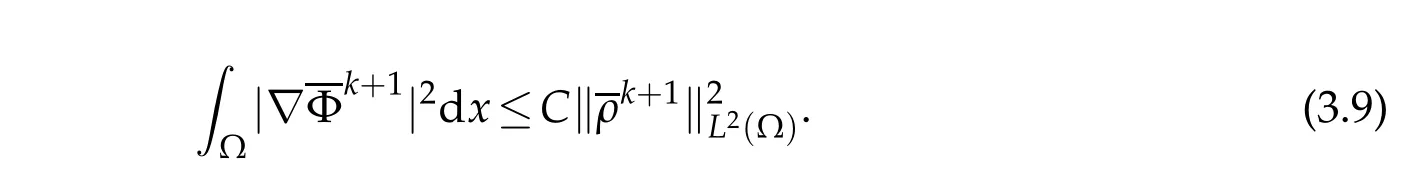
Fu rtherm ore,d ifferen tiating(2.5)in w hich one increases the index k and k+1w ith respect to tim e,respectively,m u ltip lying them byΦkandΦk+1,then integrating overΩ,w e can easily deduce that

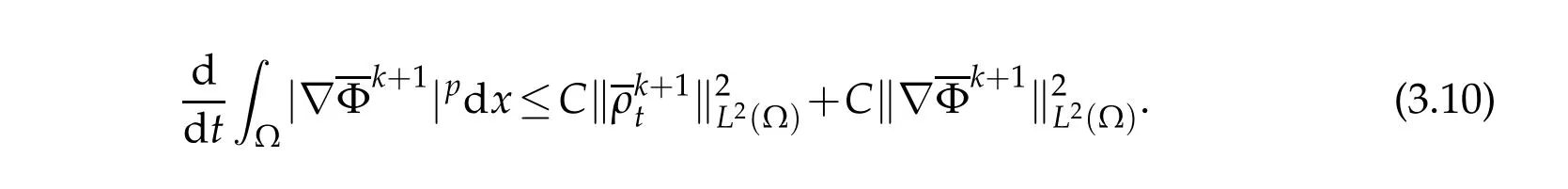
Hence by virtue of Young,s inequality,w e have

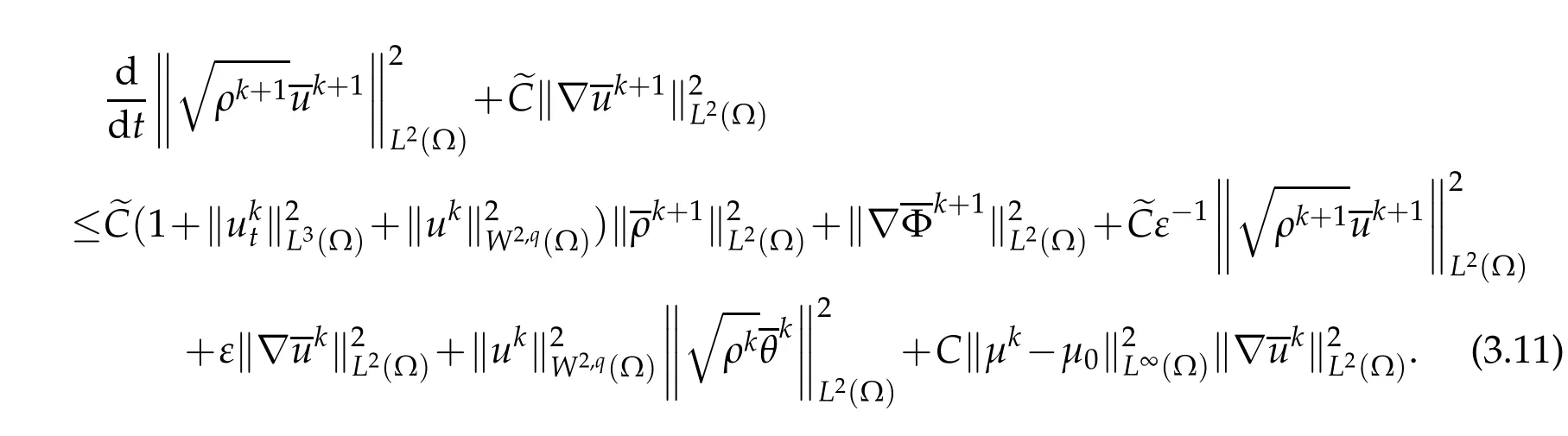
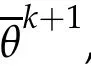
By virtue of Young,s inequality and(3.3),w e have

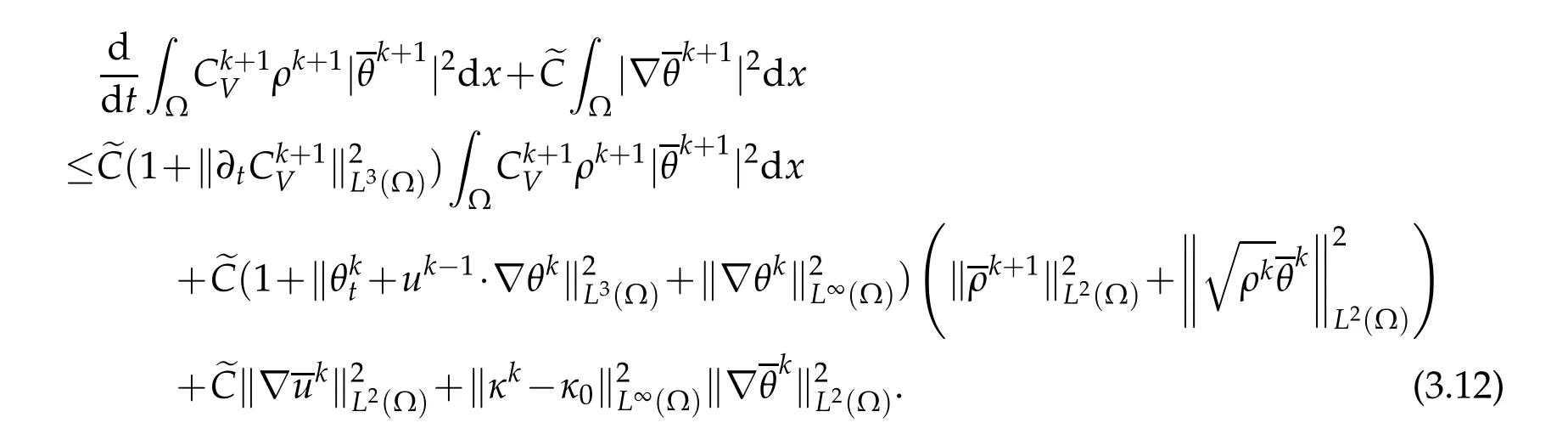
Now for a sm all fixedε＞0,letus define YkandΨkby

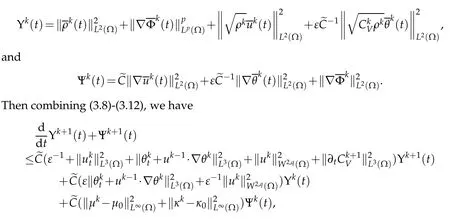
w hich im p lies in view of Gronw all,s inequality that

From(3.13),w e easily deduce that in[9]

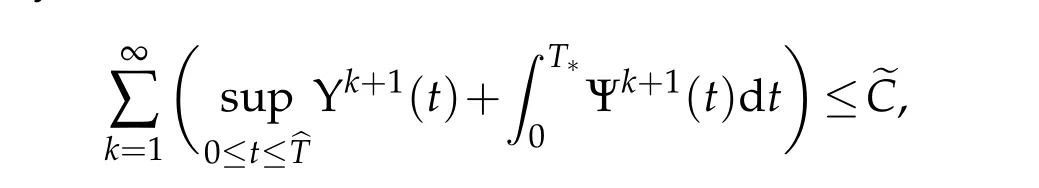
w hich obviously im p lies that

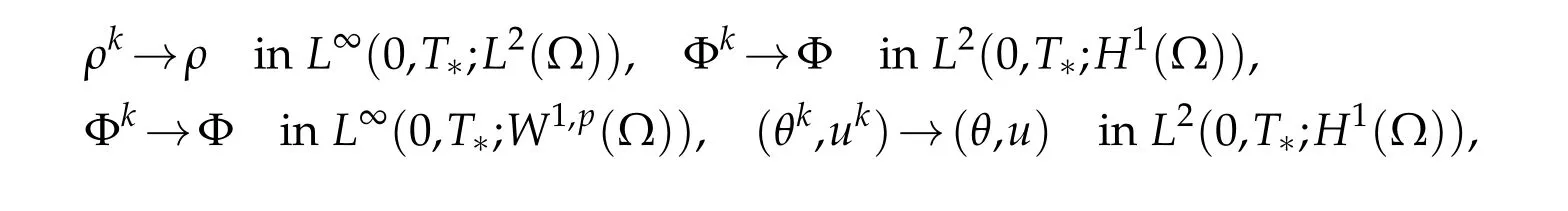
as k→∞for som e lim itsρ,u,θandΦ.By virtue of this strong convergence,one easily verifies that(ρ,θ,u,Φ)is aw eak solution to the originalnon linear p roblem(1.1)-(1.7)for som e p ressu re P.M oreover,it follow s from(2.25)-(2.28)that

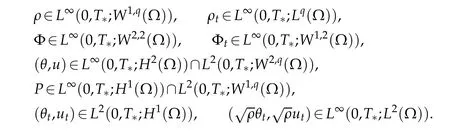
Then adap ting the argum ents of[9],w e can easily p rove the continuity in tim e of the solu tion(ρ,u,θ,P,Φ).The p roofof uniqueness is sim ilar to the calcu lations above and w e om it the details here.

[1]Fernandaz-Cara E.,Guilleu F.,The existence of nonhom ogeneous,viscous and incom p ressible flow in unbounded dom ains.Comm.PartialD ifferential Equations,17(1992),1253-1265.

[2]Choe H.J.,Kim H.,Strong solutions of the Navier-Stokes equations for nonhom ogeneous incom p ressible fluids.Comm.PartialDifferential Equations,28(2003),1183-1201.

[3]Sim on J.,Nonhom ogeneous viscous incom p ressible fluids:existenceofvelocity,density and p ressu re.SIAM J.M ath.Anal.,21(1990),1093-1117.

[4]Kim J.U.,Weak solu tionsofan initialboundary value p roblem for an incom p ressible viscous fluid w ith nonnegative density.SIAM J.M ath.Anal.,18(1987),89-96.

[5]Padu la M.,On the existence and uniqueness of non-hom ogeneousm otions in exterior dom ains.M ath.Z.,203(1990),581-604.

[6]SalviR.,The equationsof viscous incom p ressible non-hom ogeneous fluids:on the existence and regu larity.J.Aust.M ath.Soc.,B 33(1991),94-110.

[7]Tem am R.,Navier-Stokes Equations:Theory and Num erical Analysis,North-Holland,Amsterdam,1984.

[8]Cho Y.,Kim H.,Uniquesolvability for thedensity-dependentNavier-Stokesequations.Nonl. Anal.,59(2004),465-489.

[9]Cho Y.,Kim H.,Existence resu lt for heat-conducting viscous incom p ressible fluidsw ith vacuum.J.Korean M ath.Soc.,45(2008),645-681.

[10]Feireisl E.,Dynam icsof Com p ressible Fluids,Oxford University Press,2004.

[11]Lions P.L.,M athem atical Topic in Fluid Dynam ics,Vol.2,Com p ressible M odels,Oxford Science Publication,Oxford,1998.

[12]Gald i G.P.,An Introduction to the M athem atical Theory of the Navier-Stokes Equations, Sp ring-Verlag,New York,1994.

[13]Lions P.L.,M athem atical Topic in Fluid Dynam ics,Vol.1:Incom p ressible M odels,in:Oxford Lecture Series in M athem aticsand its App lications,10 1996.

[14]Yin J.P.,Tan Z.,Local existence of the strong solutions for the fu ll Navier-Stokes-Poisson equations.Nonl.Anal.,71(2009),2397-2415.

[15]Diperna R.J.,Lions P.L.,Ord inary d ifferential equations,transport theory and Sobolev spaces.Invent.M ath.,98(1989),511-547.

[16]Cho Y.,Choe H.J.,Kim H.,Unique solvability of the initial boundary value p roblem s for com p ressible viscous fluids.J.M ath.Pures Appl.,83(2004),243-275.

[17]Cho Y.,Kim H.,Existence resu lts for viscous polytropic fluids w ith vacuum.J.Differential Equations,228(2006),377-411.

10.4208/jpde.v27.n3.6 Sep tem ber 2014

∗Correspond ing au thor.Emailaddresses:mengqiu15@163.com(Q.M eng),hjy@j lu.edu.cn(H.Yuan)