双模量材料圆轴纯扭转时的应力与应变分析

吴 晓, 赵均海, 孙 晋, 杨立军



双模量材料圆轴纯扭转时的应力与应变分析

吴 晓*1, 赵均海2, 孙 晋1, 杨立军1

(1. 湖南文理学院 土木建筑工程学院, 湖南 常德, 415000; 2. 长安大学 建筑工程学院, 陕西 西安, 710061)

利用双模量材料圆轴扭转时纯剪切应力状态单元体, 推导出了双模量材料剪切弹性模量表达式, 求得了双模量材料圆轴扭转时轴向正应变. 通过分析发现: 各向同性材料圆轴纯扭转时轴向正应变为零, 而双模量材料圆轴纯扭转时轴向正应变却不为零, 双模量材料圆轴纯扭转时轴向正应变的大小主要受拉压弹性模量、拉压泊松比的影响. 双模量材料圆轴纯扭转时轴向正应变不为零的原因是: 双模量材料的拉压弹性模量、拉压泊松比均不相等, 这是双模量材料固有的特点, 也是双模量材料与各向同性材料的不同之处. 因此, 提出了双模量材料圆轴纯扭转时的平面假设: 双模量材料圆轴扭转变形前, 原为平面的横截面变形后仍保持为平面, 形状不变, 半径仍保持为直线.

双模量; 材料; 扭转; 剪切; 应变; 平面假设

众所周知, 铸铁、混凝土等材料都具有拉压弹性模量不同的双模量特性, 现已有很多文献对双模量材料结构在外载荷作用下的变形进行了计算分析. 文献[1—2]采用有限元法分析了双模量材料板的变形; 文献[3]研究了双模量泡沫材料的等效弹性模量; 文献[4]研究双模量材料的本构关系; 文献[5—10]对双模量材料结构的弯曲变形进行了计算分析; 文献[11—12]研究了双模量梁的弯曲变形; 文献[13]证明了轴向载荷对双模量梁中性轴位置有较大影响. 文献[14]在分析双模量材料结构时, 为了简化计算, 作了假设: 双模量材料拉伸弹性模量与泊松比的比值等于压缩弹性模量与泊松比的比值. 事实上, 很多双模量材料并不满足文献[14]的假设. 本文在摒弃文献[14]假设的基础上, 分析了双模量材料圆轴扭转变形时的应力与应变.

1 双模量材料剪切弹性模量

在实际工程中, 由于结构受力多以平面应力状态居多, 所以本文仅以双模量材料结构的平面应力状态为例, 讨论其应力与应变关系. 当双模量材料结构处于平面应力状态, 其受力单元体如图1所示.

图1 双模量材料单元体

对于图1所示双模量材料平面应力状态单元体, 可知其应力与应变关系分别为:

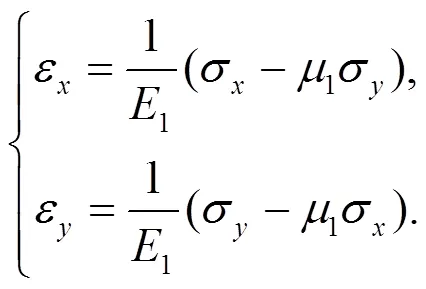
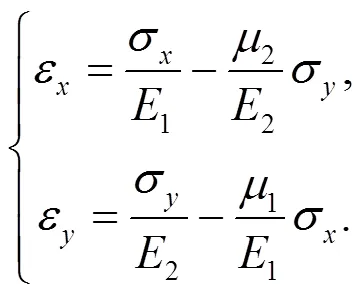
式中,1、1分别为拉伸弹性模量和泊松比;2、2分别为压缩弹性模量和泊松比.

对各向同性材料圆轴纯扭转进行分析时, 文献[15]平面假设: 圆轴扭转变形前, 原为平面的横截面变形后仍保持为平面, 形状和大小不变, 半径仍保持为直线; 且相邻两截面间的距离不变. 文献[16]平面假设: 两圆周线绕杆轴线相对旋转了一个角度, 圆周线的大小和形状均未改变; 在变形微小的情况下, 圆周线的间距也未变化. 文献[17]平面假设: 圆杆的横截面象刚体一样绕纵轴旋转, 其半径仍保持直线, 横截面仍保持圆形. 此外, 如果杆的总扭转角很小, 杆长和其半径均不会改变.

本文对图2(a)所示双模量材料圆轴纯扭转进行分析时, 作如下平面假设: 圆轴扭转变形前, 原为平面的横截面变形后仍保持为平面, 形状不变, 半径仍保持为直线.

图2(a)所示双模量材料圆轴扭转时, 可知其受力单元体为图2()所示纯剪切状态, 所以由材料力学理论可以得到:

利用式(2)或式(3)及式(5)可以求得:

由材料力学应变公式可得以下各式:

利用式(6)、(7)可以求得:

由于γ=/, 所以双模量材料剪切弹性模量为:

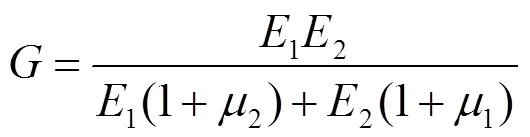
利用式(7)、(8)有:

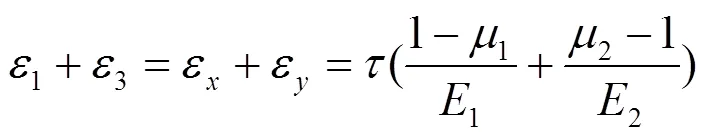
所以, 由式(11)可以求得:

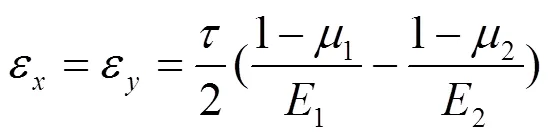
2 双模量圆轴扭转时平面假设

对式(12)进行分析可知, 图2所示双模量材料圆轴纯扭转时, 双模量材料圆轴纯扭转时轴向正应变是不为零的, 双模量材料圆轴扭转时轴向正应变为式(12)中的ε=((1-1)/1-(1-2)/2)/2. 由于有机玻璃是典型的双模量材料, 下面以有机玻璃为例来分析1/1=2/2对双模量材料圆轴纯扭转时轴向正应变的影响. 有机玻璃的材料参数为:1= 172 GPa,1= 0.34,2= 295 GPa,2= 0.395. 把有机玻璃的材料参数代入式(12)可得:ε=((1-1)/1-(1-2)/2)/2 = 0.089 3× 10-5. 把有机玻璃的材料参数代入式(12), 并假设1/1=2/2, 有ε'=(1/1-1/2)/2 = 0.121 2× 10-5. 对比以上计算结果, 可知两者相对误差为(ε'-ε)/ε= 35.72%. 这说明假设1/1=2/2时, 对相关双模量材料圆轴纯扭转时轴向正应变带来的误差影响是非常大的. 所以, 研究双模量材料圆轴纯扭转时, 为了简化计算, 假设1/1=2/2是不合理的.

图2 双模量扭转模型

现有文献对双模量材料结构在外载荷作用下变形进行计算分析时, 都沿用弹性理论研究各向同性材料结构外载荷作用下变形时所作的基本假设. 文献[15—17]研究各向同性材料圆轴纯扭转作的平面假设在本质上是相同的. 文献[15]作的平面假设是默认了圆轴纯扭转变形很微小, 所以相邻两截面间的距离不变. 文献[16]作的平面假设是: 在变形微小的情况下, 圆周线的间距也未变化. 文献[17]作的平面假设是: 如果杆的总扭转角很小, 杆长和其半径均不会改变. 显然本文的研究结果表明, 文献[15—17]研究各向同性材料圆轴纯扭转作的平面假设, 对研究双模量材料圆轴纯扭转已不适用.

由于扭转的平面假设是研究圆轴纯扭转的基础, 所以本文对双模量材料圆轴纯扭转时的应力与应变计算结果进行分析, 并把双模量材料圆轴纯扭转时的应力与应变计算结果与文献[14]研究双模量材料纯剪切状态时的结论进行比较, 提出了双模量材料圆轴纯扭转时的平面假设: 双模量材料圆轴扭转变形前, 原为平面的横截面变形后仍保持为平面, 形状不变, 半径仍保持为直线. 本文的研究为进一步深入分析双模量材料圆轴的扭转奠定了基础.

3 结论

① 推导出了双模量材料剪切弹性模量表达式.

② 假设1/1=2/2, 对相关双模量材料圆轴纯扭转时轴向正应变带来的误差影响是非常大的. 所以, 研究双模量材料圆轴纯扭转时, 为了简化计算, 假设1/1=2/2是不合理的.

③ 双模量材料圆轴纯扭转时轴向正应变不为零. 双模量材料圆轴纯扭转时轴向正应变不为零的原因是: 双模量材料圆轴纯扭转时轴向正应变的大小主要受拉压弹性模量、拉压泊松比的影响,双模量材料的拉压弹性模量、拉压泊松比均不相等, 这是双模量材料固有的特点, 也是双模量材料与各向同性材料的不同之处.

④ 提出了双模量材料圆轴纯扭转时的平面假设: 双模量材料圆轴扭转变形前, 原为平面的横截面变形后仍保持为平面, 形状不变, 半径仍保持为直线.

[1] Medri G. A. nonlinear elastic model for isotropic materials with different behavior in tension and compression [J]. Transactions of the ASME, 1982, 26: 26—28.

[2] Srinivasan R S, Ramachandra L S. Axisymmetric nonlinear dynamic response of bimodulous annular plates [J]. Journal of Vibration and Acoustics, 1990, 112(2): 202—205.

[3] 李战莉, 黄再兴. 双模量泡沫材料等效弹性模量的细观力学估算方法[J]. 南京航空航天大学学报, 2006, 38(4): 464—468.

[4] 蔡来生, 俞焕然. 拉压模量不同弹性物质的本构[J]. 西安科技大学学报, 2009, 29(1): 17—21.

[5] 吴晓, 杨立军, 孙晋. 双模量圆板弯曲变形的计算分析[J]. 西安建筑科技大学学报: 自然科学版, 2009, 41(1): 88—92.

[6] 吴晓, 黄翀, 杨立军, 等. 拉压模量不同圆板的非线性弯曲计算[J]. 工程力学, 2011, 28(4): 23—27, 57.

[7] 吴晓, 杨立军, 黄翀. 双模量矩形板的大挠度弯曲计算分析[J]. 工程力学, 2010, 27(1): 17—22.

[8] 吴晓, 杨立军. 双模量面板泡沫铝芯夹层圆板的非线性弯曲[J]. 工程力学, 2011, 28(11): 12—16.

[9] 吴晓, 杨立军, 黄翀, 等. 用能量法研究双模量大挠度圆板的轴对称弯曲[J]. 计算力学学报, 2011, 28(2): 274—278.

[10] 吴晓. 用Kantorovich及Galerkin联合法研究双模量板的弯曲[J]. 西安建筑科技大学学报: 自然科学版, 2012, 44(4): 457—461.

[11] 吴晓, 杨立军. 拉压弹性模量不同曲梁的弹性理论解[J]. 工程力学, 2013, 30(1): 76—80.

[12] 周小平, 卢萍, 张永兴, 等. 不同拉压模量弹性地基梁的解析解[J]. 重庆大学学报: 自然科学版, 2007, 30(7): 78—82.

[13] 姚文娟, 叶志明. 不同模量弯压柱的解析解[J]. 应用数学和力学, 2004, 25(9): 901—909.

[14] 阿巴尔楚米扬. 不同模量弹性理论[M]. 北京: 中国铁道出版社, 1986: 18—19.

[15] 孙训方, 方孝淑, 关来泰. 材料力学(I)[M]. 4版. 北京: 高等教育出版社, 2002: 57.

[16] 刘鸿文. 材料力学(上册)[M]. 北京: 高等教育出版社, 1999: 98.

[17] S 铁摩辛柯, J 盖尔. 材料力学[M]. 北京: 科学出版社, 1990: 80.

Analysis of stress and strain for circular shaft with bimodular materials in torsion

WU Xiao1, ZHAO JunHai2, SUN Jin1, YANG LiJun1

(1. College of Civil and Architecture Engineering, Hunan University of Arts and Science, Changde 415000, China; 2. School of Civil and Engineering, Changan University, Xi’an 710061, China)

Using the pure shear stress state element of circular shaft with bimodulus materials in torsion, the shear modulus expression is derived, and then the axial normal strain of circular shaft with bimodulus materials in torsion is obtained. And the analysis shows that the normal strain was zero of circular shaft in torsion with isotropic properties materials, while the normal strain was not zero with bimodulus materials. And the axial normal strain of circular shaft with bimodulus materials in torsion was mainly controlled by the tensile and compressive elastic modulus, tensile and compression Poisson ratio. The reason of axial normal strain being not zero is as follow: elastic modulus of tension and compression, tension and compression Poisson ratio are not equal. So this is the characteristic of bimodulus material, and which is different from isotropic properties materials. Therefore, the hypothesis is proposed of circular shaft with bimodulus materials in torsion: the cross section of circular shaft with bimodulus materials in torsion remains plane, and its shape remains same, radius remains as a straight line.

bimodulous; materials; torsion; shear, strain; plane assumption

10.3969/j.issn.1672-6146.2014.03.015

O 341

1672-6146(2014)03-0063-04

email: wx2005220@163.com.

2014-03-26

湖南省“十一五”重点建设学科资助(湘教通[2006]180号)

(责任编校: 江 河)