从哈密顿原理推导正则变换条件的几个概念问题

陈国贵, 龚善初, 黄亦斌



从哈密顿原理推导正则变换条件的几个概念问题

陈国贵1, 龚善初*1, 黄亦斌2

(1. 揭阳职业技术学院 机电工程系, 广东 揭阳, 522000; 2. 江西师范大学 物理与通信电子学院, 江西 南昌, 330027)

本文厘清了从哈密顿原理推导正则变换条件的几个基本概念问题, 澄清了一些误解, 并给出了正确的推导过程.

哈密顿原理; 正则变换; 相空间

哈密顿原理和正则变换是理论力学中的重要内容. 后者的条件也可从前者导出, 故二者存在紧密联系. 然而在从哈密顿原理推导正则变换条件的过程中, 笔者发现不少著述都存在一定问题.

1 用于推导正则变换条件的哈密顿原理不是通常的哈密顿原理

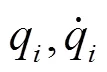
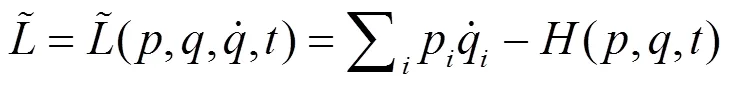
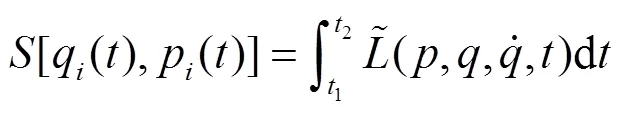
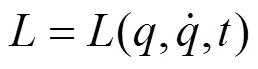
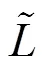
这一点也可以从物理角度来理解. 固定相空间中的一点就是给定初位置和初速度, 那么此后的真实相轨道就完全确定了. 它显然不一定能通过预先给定的相空间中的另一点, 从而固定相空间中的2点一般找不到真实轨道. 与此相反, 位形空间中通过任意2点总有真实轨道存在, 这是因为此时只是给定了初位形, 还可以调节初速度使得在一定时刻到达给定的末位形. 因此, 在“修改的哈密顿原理”中, 并不要求、也不能要求相空间中始末端的完全固定, 只要求其部分正则变量——广义坐标固定. 所以, 在相空间中边界条件的形式只能是由给定时刻的q(1)和q(2)所确定的2个超曲面, 而不能是2个点.

2 正则变换条件的正确推导

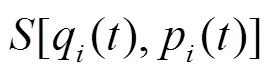
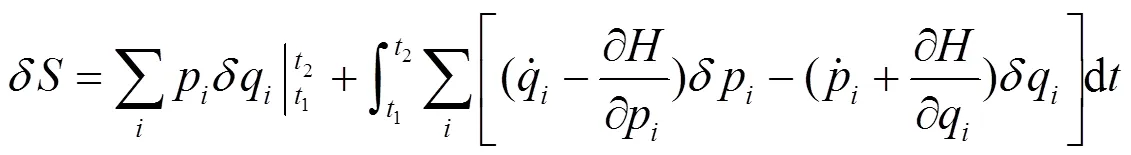
根据修改的哈密顿原理, 考虑到边界条件, 可得正则方程:

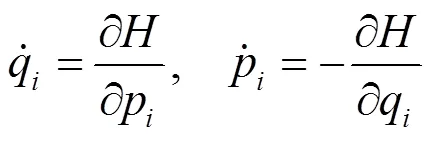
根据正则变换的含义, 希望找到一组新变量

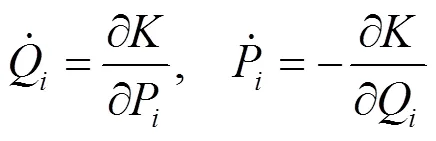
由于原正则方程可由作用量的变分导出, 故新正则方程也应涉及新作用量:

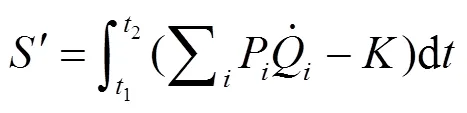
的变分:

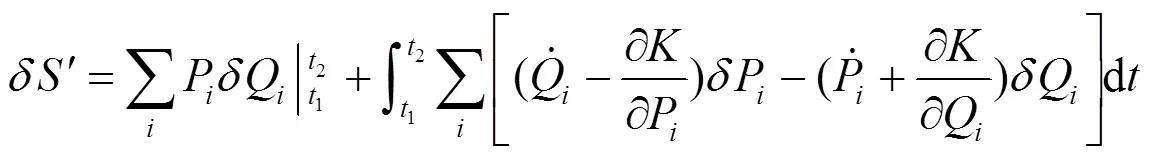
由于只要求式(3)中的积分项为0能保证式(8)中的积分项为0, 所以两作用量可相差一边界项:

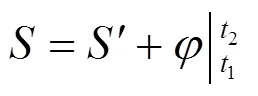
或者说, 两被积函数可相差一全导数:

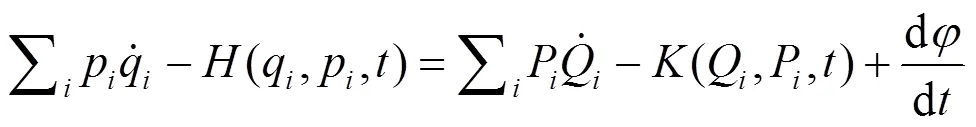
或

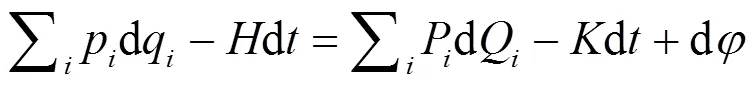
现在, 由式(8)、式(9)得:

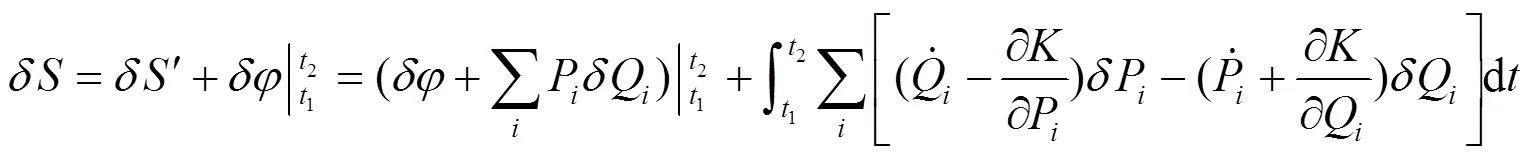
由式(11), 考虑等时变分, 有:

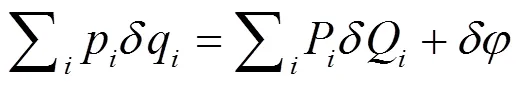
故式(12)可以写为:

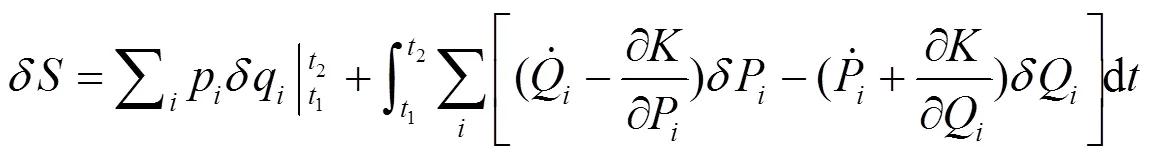
3 系统取真实相轨道时新作用量可不取驻值

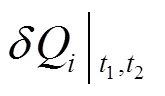
先看边界条件. 由相空间中的一般变换式(5)知:

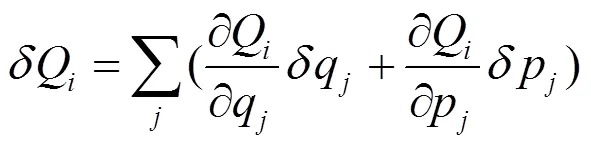
4 正则变换的条件还可放宽

关键在于式(9). 两作用量不仅可相差一个边界项, 还可相差一个倍数:

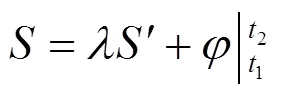
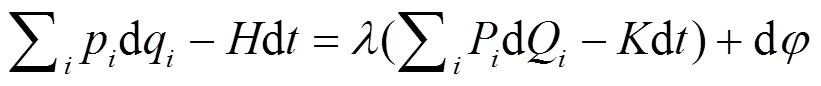
[1] Wu TaYou. Classical Mechanics: Langrangian and Hamiltonian Dynamics[M]. Taipei: Lein-King Publ Co, 1977.

[2] 陈滨. Hamilton原理四种表达形式的异同[J]. 力学与实践, 1994, 16(1):64—68.

[3] 陈滨. 正则空间Hamilton原理的一个性质[A]. 振动与控制的研究[C]. 北京: 北京大学出版社, 1994.

[4] 朱如曾. 关于哈密顿原理的两种不变性问题[J]. 力学与实践, 1994, 16(4): 63—67.

[5] 陈滨. 论Hamilton作用量的极值性质[J]. 商丘师范学院学报,1997, 13(1): 1—19.

[6] 朱如曾. 非完整力学的第二类、第一类和中间类型变分原理[J]. 中国科学A辑, 1999, 29(1): 49—54.

[7] 格林伍德D T. 经典动力学[M]. 北京: 科学出版社, 1982: 211—212.

Some conceptual problems in deduction of condition of canonical transformation by Hamilton’s principle

CHEN GuoGui1, GONG ShanChu1, HUANG YiBin2

(1. Department of Electronic Engineering, Jieyang Vocational and Technical College, Jieyang 522000, China; 2. Department of Physics, Jiangxi Normal University, Nanchang 330027, China)

Some conceptual problems in deduction of condition of canonical transformation by Hamilton’s principle are clarified, and some misunderstanding about it are pointed out. The correct deduction is given.

Hamilton’s principle; canonical transformation; phase space

10.3969/j.issn.1672-6146.2014.03.003

O 316

1672-6146(2014)03-0011-04

email: gsc@jyc.edu.cn.

2014-03-27

(责任编校:刘刚毅)