受水压作用下隧道围岩压力的非线性上限分析
2014-05-13唐小富莫林辉谢文祥
唐小富, 莫林辉, 谢文祥
受水压作用下隧道围岩压力的非线性上限分析
唐小富*, 莫林辉, 谢文祥
(湖南省永龙高速公路建设开发有限公司,湖南 永顺, 416700)
针对浅埋隧道, 在非线性破坏准则下, 根据虚功率原理求解了围岩压力的上限解, 并分析了不同因素对围岩压力的影响. 研究结果表明: 岩土材料破坏准则的非线性、地表荷载、孔隙水以及埋深对浅埋隧道的围岩压力都有较大的影响, 尤其是决定岩土材料抗剪强度参数的非线性系数; 另外, 侧压力系数较小时, 边墙的围岩压力较小, 而顶部的围岩压力却很大, 则此时需要注意和加强浅埋隧道顶部的支护措施, 防止发生冒顶事故.
浅埋隧道; 非线性破坏准则; 极限分析; 围岩压力
围岩压力的确定直接关系到浅埋隧道支护的设计以及稳定性的分析. 目前, 关于围岩压力的计算方法主要是极限平衡法, 如公路隧道设计规范. 但是, 由于极限平衡法并没有考虑到土体的本构关系, 再加上工程地质条件的复杂性, 因此, 对于复杂的地质条件, 想通过极限平衡法来得到围岩压力的准确解具有一定的困难. 而极限分析法却刚好弥补了这一缺陷, 即考虑了土体的本构关系, 从能量的角度出发, 并且还可以结合复杂的地质条件去研究工程的稳定性[1]. 于是, 极限分析法得到了广泛的应用, 尤其是关于边坡的稳定性问题. 最近, 一些学者将极限分析法应用到隧道工程中, 伍良波等[2]针对浅埋隧道构建了2种平动破坏模式, 并且通过围岩压力的对比, 验证了极限分析法应用在隧道工程中的可行性; 采用极限分析法推导了浅埋隧道围岩压力和稳定性系数的解析解, 并且还得到了埋深比对围岩压力的影响规律. 谢骏等[3]构建了双平行浅埋隧道的破坏机制, 并且运用极限分析法得到了不同净距下的稳定率. 王建新等[4]运用有限元极限分析法研究了海底隧道的稳定性, 并且还分析了破碎带对安全系数的影响. 上述研究都假定土体服从线性Mohr-Coulomb破坏准则, 而事实上, 土体破坏时服从非线性Mohr-Coulomb破坏准则, 且线性破坏准则只是其中一种特殊情况[5—20]. 因此, 本文基于非线性Mohr-Coulomb破坏准则, 采用极限分析法研究各种不利因素对浅埋隧道围岩压力的影响, 为今后浅埋隧道的支护设计提供理论依据和指导.
1 极限分析非线性理论
1.1 非线性Mohr-Coulomb破坏准则
在塑性理论中, 一般认为土体服从线性Mohr-Coulomb破坏准则, 但是大量实验证明, 土体发生破坏时, 剪应力与正应力呈非线性关系, 即土体服从非线性Mohr-Coulomb破坏准则, 而线性破坏准则只是其中一种特殊情况, 具体的表达式为[5—20]:
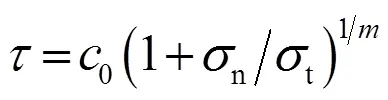
式中,和n分别为剪应力和正应力;0为初始粘聚力;t为轴向拉应力;为非线性系数. 另外, 当= 1时, 非线性破坏准则就转换成了线性破坏准则.
在直角坐标系中, 过非线性破坏准则这条曲线作一条切线, 则此切线的表达式为:
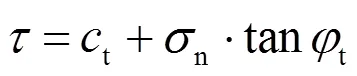
式中,t与tant分别为切线的截距与斜率.
由式(1)和式(2)可得, 非线性破坏准则下土体抗剪强度参数为:
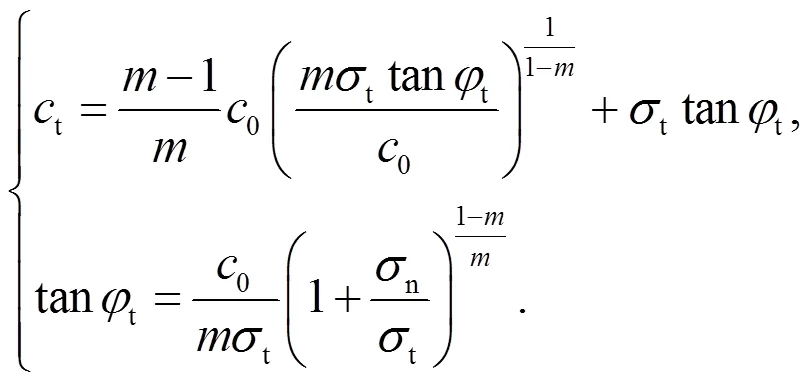
1.2 极限分析上限定理
Chen在研究极限分析上限定理时认为, 在机动容许的速度场中, 如果满足速度边界条件以及应变与速度相容条件, 则根据外功率与内功率相等所得到的荷载一定不小于极限状态下的真实荷载, 且具体表达式为[5—20]:
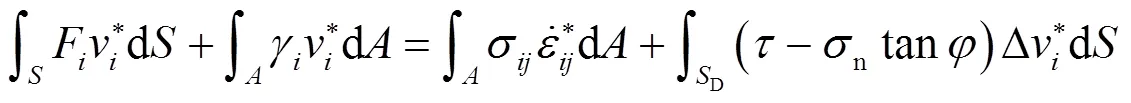
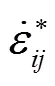
杨小礼将非线性破坏准则引入到极限分析上限定理中, 提出了极限分析非线性理论, 从而使得极限分析上限定理更加严谨、完善. 因此, 本文基于极限分析非线性理论来求解各种不利因素下浅埋隧道围岩压力的上限解, 在计算过程中, 将式(3)代入式(4)所求得的解必定是真实值的一个上限解.
2 围岩压力计算
2.1 破坏模式
求解浅埋隧道围岩压力上限解的关键是构建满足速度相容的破坏模式. 文献[6]针对纯粘土提出了浅埋圆形隧道的破坏模式, 本文结合库仑材料的特点作了进一步的改进, 即基于已有的研究成果, 针对库仑材料构建了浅埋隧道的平动破坏模式以及相容速度场, 浅埋隧道的破坏模式和速度场如图1所示, 其中, 图1(a)为浅埋隧道的破坏模式, 即由一个四边形刚块体以及两三角形刚块体、组成, 根据极限分析上限定理的要求, 刚块体在破坏过程中体积不发生变化;为隧道的埋深;为隧道的跨度和高度; 刚块体竖直向下运动, 速度为0; 两个三角形刚块体、的速度为1;01为速度场中两相邻刚块体之间的相对速度;s为地表荷载;为孔隙水压力;和分别为隧道顶部和边墙的围岩压力. 图1(b)为破坏模式中的相容速度场.
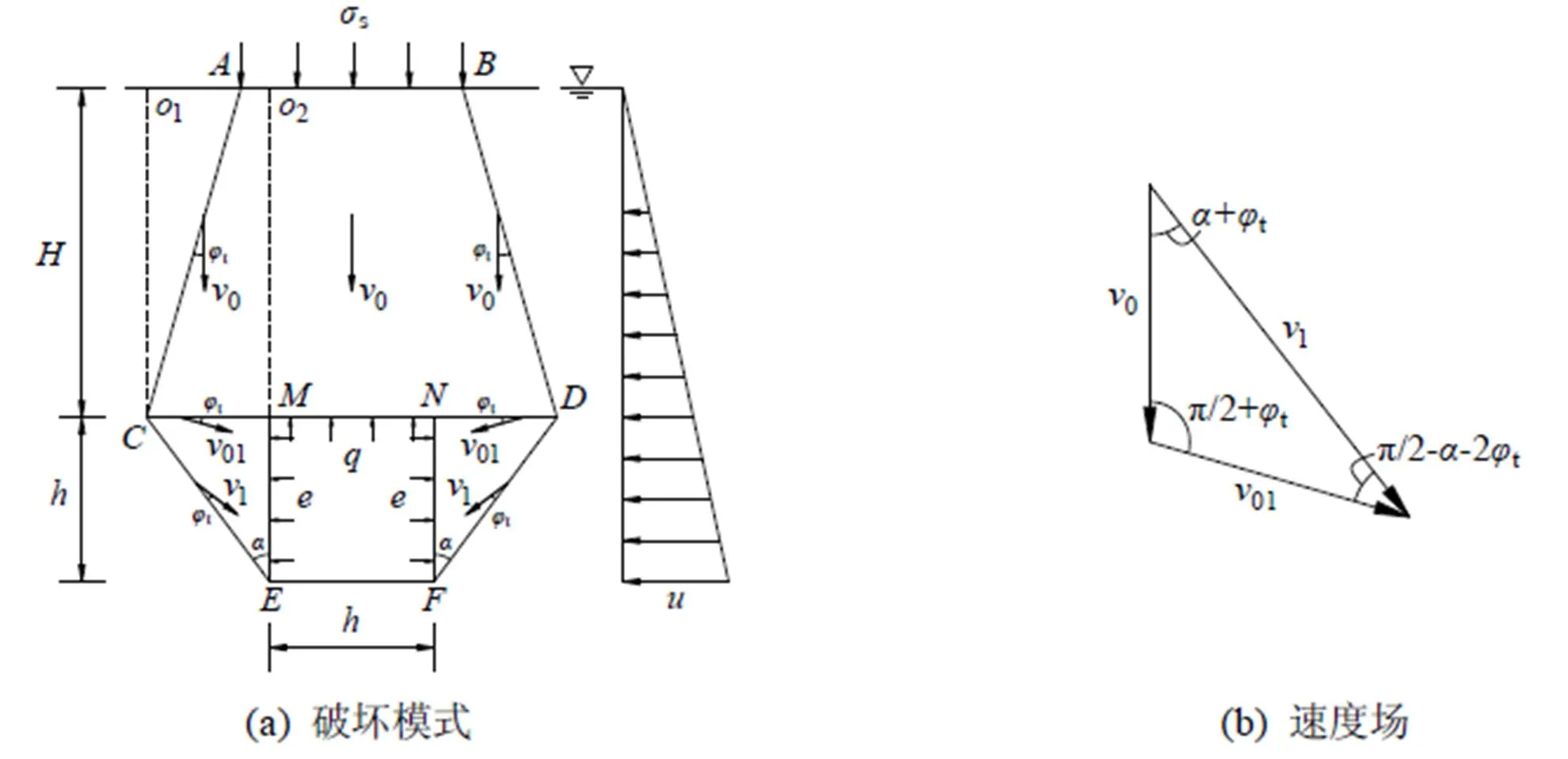
图1 浅埋隧道的破坏模式和速度场
2.2 计算过程
由于浅埋隧道的破坏模式左右对称, 为简化计算, 取一半结构(左半结构)进行研究.
① 间断线的速度、长度以及滑块的面积.
根据图1中的几何关系可以得到各间断线的速度、长度以及滑块的面积见以下各式:
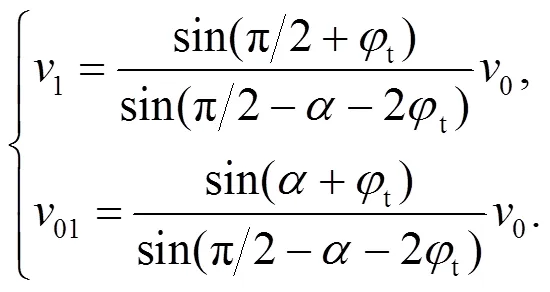
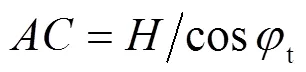
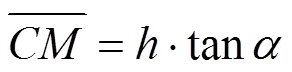
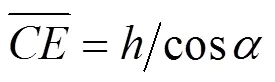
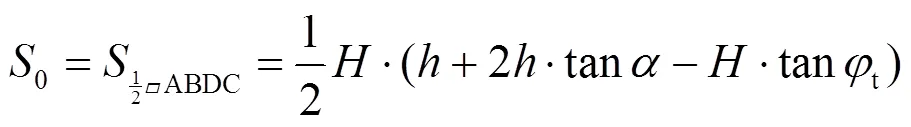
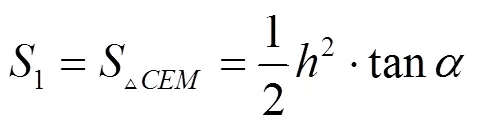
②外功率.
在浅埋隧道中, 外力产生的功率包括土体重力、支护力、地表荷载及孔隙水压力所做的功率, 具体表达式如下.
土体重力做的功率:
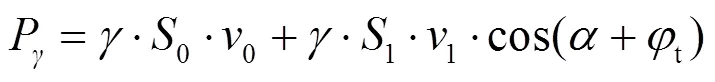
支护力做的功率:
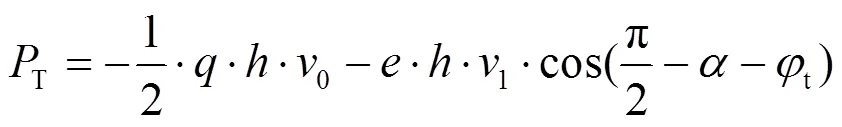
地表荷载做的功率:
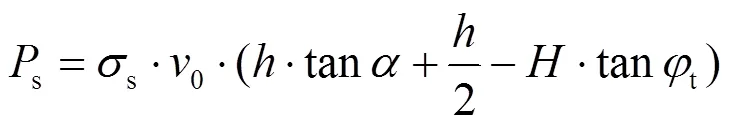
根据Bishop的观点, 将孔隙水压力看作外力, 其大小与土体的自重应力呈比例关系, 具体表达式为:
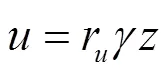
由于假定刚性块体的体积在破坏过程中不发生变化, 则孔隙水压力只在边界上做功, 结合图1(a)有:
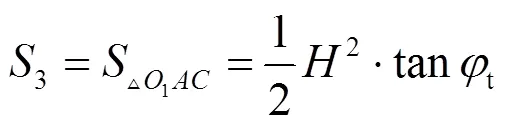
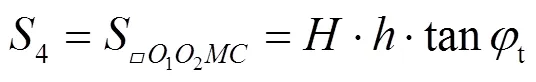
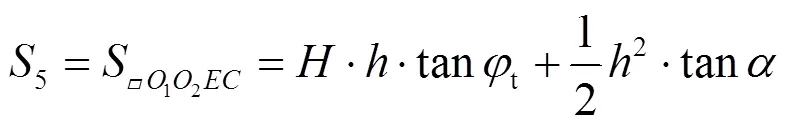
故孔隙水压力做的功率:
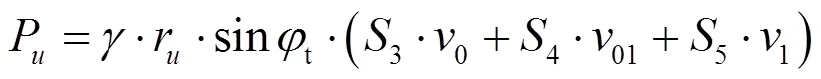
③内能耗散率.
由于假定在破坏过程中刚性块体的体积不变, 则内能耗散率只发生在间断线上, 故间断线上的内能耗散率为:
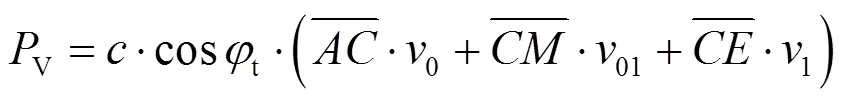
④围岩压力的上限解.
根据极限分析上限定理, 联立式(11)、(12)、(13)、(18)、(19)可得围岩压力的上限解为:

由式(20)可得, 围岩压力是关于变量的函数. 欲求围岩压力的最小上限解, 则可以将其计算转化为一个数学优化模型. 换言之, 在满足约束条件式(21)的前提下, 求解目标函数=()的最小值, 而此最小值正是围岩压力的最小上限解.
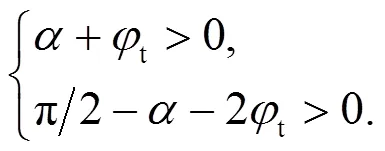
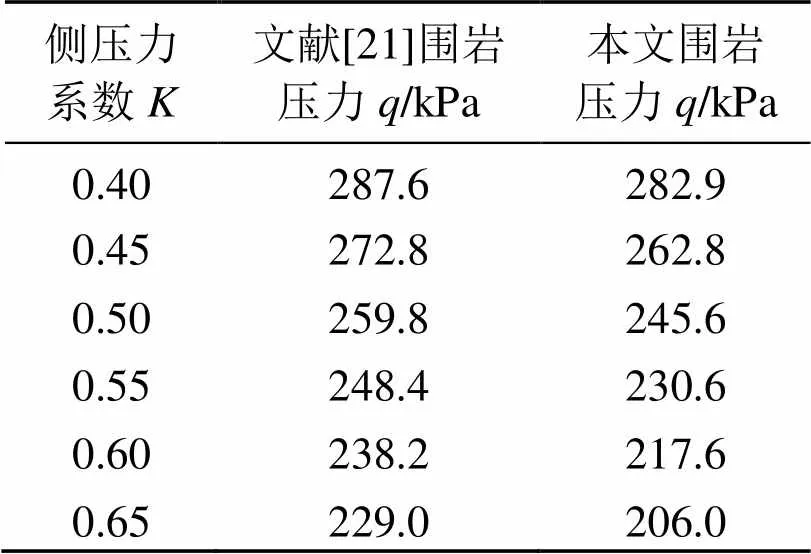
表1 围岩压力上限解的对比
3 结果对比与分析
3.1 与已有研究成果的对比
文献[21]应用极限分析上限定理得到了线性破坏准则下浅埋隧道围岩压力的上限解.
为了进行对比, 本文令非线性系数= 1, 即将非线性破坏准则转换成线性破坏准则, 其他条件简化相同, 具体参数为: 隧道埋深= 20 m; 隧道的跨度和高度= 10 m; 土体重度= 20 kN/m3; 粘聚力= 10 kPa; 内摩擦角= 18°.
在相同条件下, 将本文所得到的围岩压力的上限解与文献[21]所得结果进行了对比, 对比见表1. 由表1可得, 在不同侧压力系数的情况下, 本文所得到的计算结果非常接近于文献[21]的结果, 从而验证了本文的正确性.
3.2 参数分析
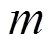
如图2(a)所示, 在埋深= 20 m, 且无地表荷载和孔隙水压力的条件下, 当系数一定时, 随着非线性系数的增大, 围岩压力呈明显增大的趋势. 这说明了围岩较差的地段, 浅埋隧道所需要的支护力较大, 在开挖时应注意加强支护措施. 当非线性系数一定时, 随着系数的减小, 围岩压力呈增大的趋势. 由此可得, 当系数较小时, 由于浅埋隧道两边墙处的围岩压力较小, 则顶部必须承受更大的围岩压力, 故在系数较小的情况下需要加强顶部的支护措施.
如图2(b)所示, 在埋深= 20 m、系数= 1, 且无孔隙水的条件下, 围岩压力随地表荷载s的增大而增大.
如图2(c)所示, 在埋深= 20 m、系数= 1, 且无地表荷载的条件下, 围岩压力随孔隙水压力系数r的增大而增大. 这说明了在孔隙水较丰富的地段, 浅埋隧道所需要的支护力较大, 因此必须加强监控量测及支护措施, 防止在开挖过程中发生突水突泥或坍塌事故.
如图2(d)所示, 在系数= 1, 且无地表荷载和孔隙水的条件下, 围岩压力随埋深的增大而增大. 这说明了埋深对浅埋隧道有较大的影响, 且埋深越大, 浅埋隧道所需要的支护力越大.
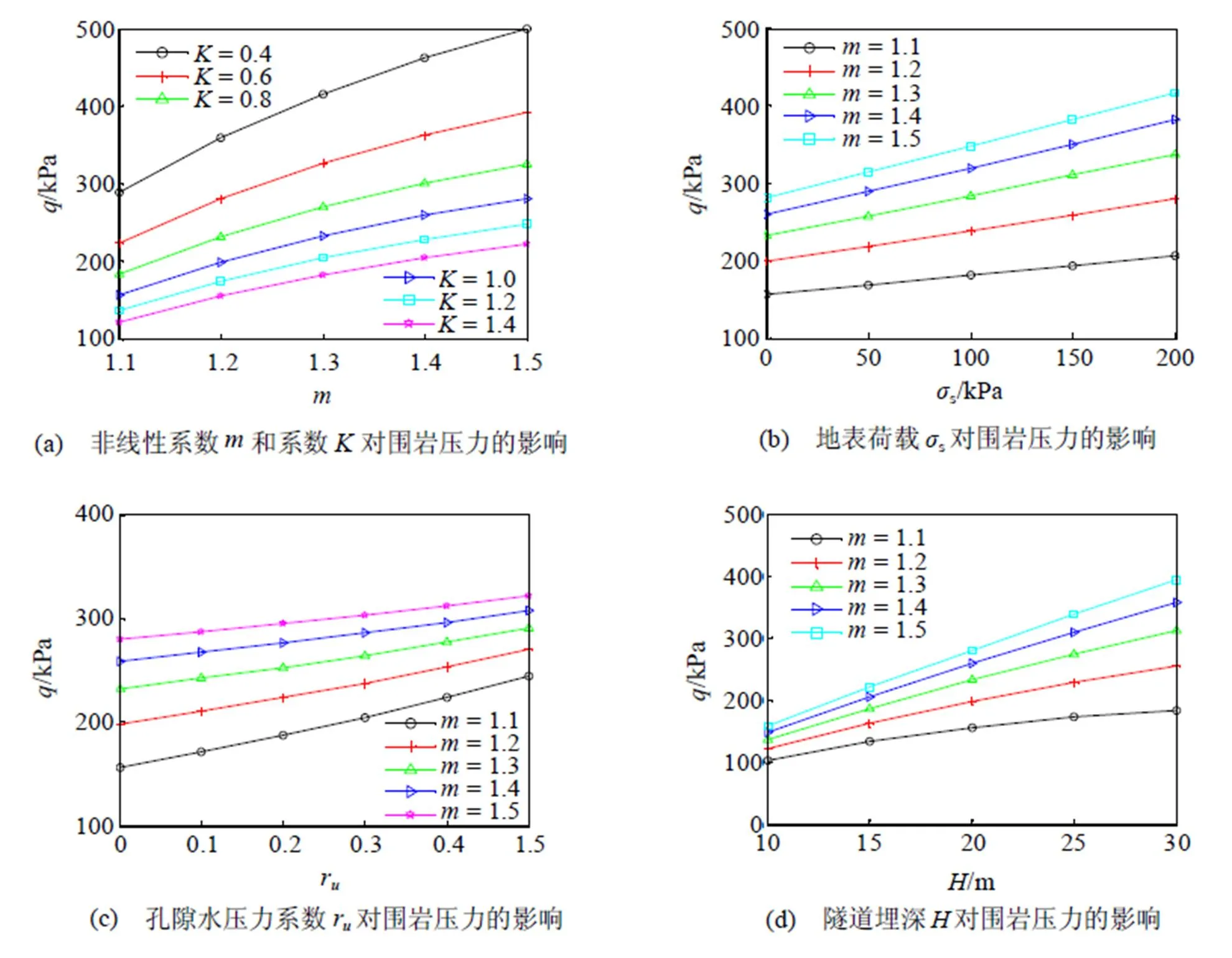
图2 不利因素对浅埋隧道围岩压力的影响
4 结论
运用极限分析非线性理论推导了浅埋隧道围岩压力的解析解, 并且将最小值的计算转换成一个数学优化模型, 借助Matlab软件得到了围岩压力的最小上限解.
在条件相同的情况下, 将本文所得到围岩压力的上限解与已有的研究成果进行了对比, 其结果的一致性验证了本文的正确性.
在非线性Mohr-Coulomb破坏准则下, 研究了各种不利因素对浅埋隧道围岩压力的影响规律. 即随着非线性系数、地表荷载s、孔隙水压力系数r、埋深的增大或者系数的减小, 浅埋隧道的围岩压力都呈增大的趋势. 因此, 对于浅埋隧道, 在围岩较差、地表荷载较大、孔隙水较丰富以及埋深较大的地段, 要注意加强监控量测和支护措施, 特别是在系数较小的位置, 更应注意加强顶部的支护措施, 避免发生坍塌事故.
[1] 徐干成, 白洪才, 郑颖人, 等. 地下工程支护结构[M]. 北京: 中国水利水电出版社, 2001: 41—45.
[2] 伍良波, 刘运思. 不同埋深比下浅埋隧道稳定性的上限分析[J]. 公路工程, 2013, 38(4): 262—264.
[3] 谢骏, 刘纯贵, 于海勇. 双平行圆形隧道稳定的塑性极限分析上限解[J]. 岩石力学与工程学报, 2006, 25(09): 1835—1841.
[4] 王建新, 王思敬, 王在泉, 等. 海底隧道稳定性分析[J]. 工程勘察, 2008(2): 4—7.
[5] Yang Xiao-li, Yang Zi-han, Pan Qiu-jing, et al. Kinematical analysis of highway tunnel collapse using nonlinear failure criterion [J]. Journal of Central South University, 2014, 21(1): 381—386.
[6] Davis E H, Gunn M J, Mair R J, et al. The stability of shallow tunnels and underground openings in cohesive material [J]. Geotechnique, 1980, 30(4): 397—416.
[7] Yang Xiao-li, Yang Zi-han, Li Yong-xin, et al. Upper bound solution for supporting pressure acting on shallow tunnel based on modified tangential technique [J]. Journal of Central South University, 2013, 20(12): 3676—3682.
[8] Yang Xiao-li, Zhang Dao-bing, Wang Zuo-wei. Upper bound solutions for supporting pressures of shallow tunnels with nonlinear failure criterion [J]. Journal of Central South University, 2013, 20(7): 2034—2040.
[9] Yang Xiao-li, Zhang Jia-hua, Jin Qi-yun, et al. Analytical solution to rock pressure acting on three shallow tunnels subjected to unsymmetrical loads [J]. Journal of Central South University, 2013, 20(2): 528—535.
[10] Yang Xiao-li, Jin Qi-yun, Ma Jun-qiu. Pressure from surrounding rock of three shallow tunnels with large section and small spacing [J]. Journal of Central South University, 2012, 19(8): 2380—2385.
[11] Yang Xiao-li, Huang Fu, Wang Jin-ming. Modified image analytical solutions for ground displacement using the nonuniform convergence model [J]. Journal of Central South University of Technology, 2011, 18(3): 859—865.
[12] Yang Xiao-li, Huang Fu. Influences of strain softening and seepage on elastic and plastic solutions of circular openings in nonlinear rock masses [J]. Journal of Central South University of Technology, 2010, 17(3): 621—627.
[13] Yang Xiao-li, Huang Fu. Stability analysis of shallow tunnels subjected to seepage with strength reduction theory [J]. Journal of Central South University of Technology, 2009, 16(6): 1001—1005.
[14] Yang Xiao-li, Zou Jin-feng. Estimation of compaction grouting pressure in strain softening soils [J]. Journal of Central South University of Technology, 2009, 16(4): 653—657.
[15] Yang Xiao-li, Huang Fu. Slope stability analysis considering the joined influences of nonlinearity and dilation [J]. Journal of Central South University of Technology, 2009, 16(2): 292—296.
[16] Yang Xiao-li, Zou Jin-feng. Displacement and deformation analysis for uplift piles [J]. Journal of Central South University of Technology, 2008, 15(6): 906—910.
[17] Yang Xiao-li, Sui Zhi-rong. Seismic failure mechanisms for loaded slopes with associated and nonassociated flow rules [J]. Journal of Central South University of Technology, 2008, 15(2): 276—279.
[18] Yang Xiao-li, Wang Jin-ming. Influences of stress dilation on shape of failure surface for shallow tunnels [J]. Journal of Central South University of Technology, 2008, 15(S1): 293—297.
[19] Yang Xiao-li, Wang Jin-ming. Stress dilatancy analysis of shallow tunnels subjected to unsymmetrical pressure [J]. Journal of Central South University of Technology, 2008, 15(S2): 28—33.
[20] Yang Xiao-li, Guo Nai-zheng, Zhao Lian-heng, et al. Influences of nonassociated flow rules on seismic bearing capacity factors of strip footing on soil slope by energy dissipation method [J]. Journal of Central South University of Technology, 2007, 14(6): 842—847.
[21] 杨小礼, 王作伟. 非线性破坏准则下浅埋隧道围岩压力的极限分析[J]. 中南大学学报: 自然科学版, 2010, 41(1): 299—302.
Upper bound analysis of surrounding rock pressure against tunnel subjected to water and nonlinear failure criterion
TANG XiaoFu, MO LinHui, XIE WenXiang
(Yonglong Expressway Construction and Development Co Ltd, Jishou 416700, China)
Aiming at the shallow rectangular tunnel, the upper bound solutions of surrounding rock pressure were solved according to the principle of virtual power, and the surrounding rock pressure was discussed based on nonlinear failure criterion. The results state that, a variety of disadvantages have great influence on surrounding rock pressure of shallow rectangular tunnel, particularly the nonlinear coefficient, which decides the shear strength parameters of geotechnical materials. Besides, surrounding rock pressure of sidewall is smaller and surrounding rock pressure of top is bigger in the case of smaller earth pressure factor, when the supporting system of top on shallow rectangular tunnel should be attended to and reinforced in order to prevent the roof fall accidents.
shallow buried tunnel; nonlinear failure criterion; limit analysis; surrounding rock pressure
10.3969/j.issn.1672-6146.2014.03.012
U 451+.2
1672-6146(2014)03-0049-06
email: 2485173649@qq.com.
2014-04-08
(责任编校: 江 河)
