一类图在环面上的嵌入
2014-05-13李万胜黄元秋张湘林刘新求
李万胜, 黄元秋, 张湘林, 刘新求
一类图在环面上的嵌入
李万胜*, 黄元秋, 张湘林, 刘新求
(湖南师范大学 数学与计算机科学学院, 湖南 长沙, 410081)
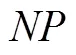
亏格; 环面; 联树
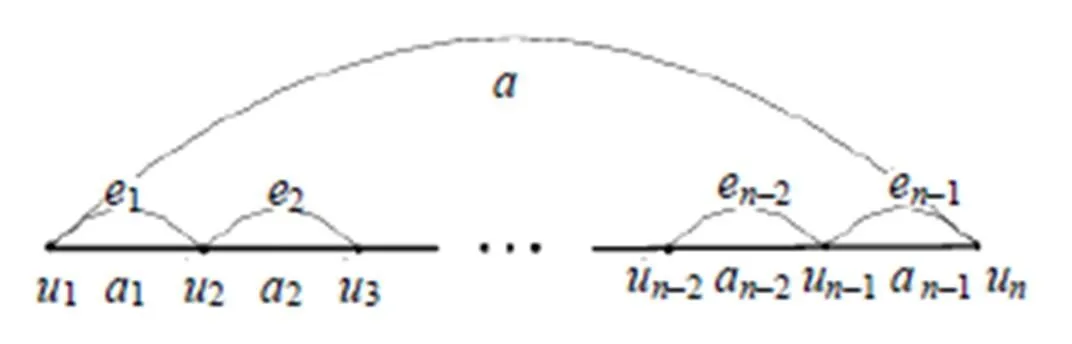
图1
1 引理

在曲面的多边形表示中, 以下3种运算并不改变曲面的类型:


证 由引理1易得.
2 主要结论
断言1 所有的余树边均为非扭边.
断言5 余树边中至少有1组边相互交错.

图2 的一棵联树
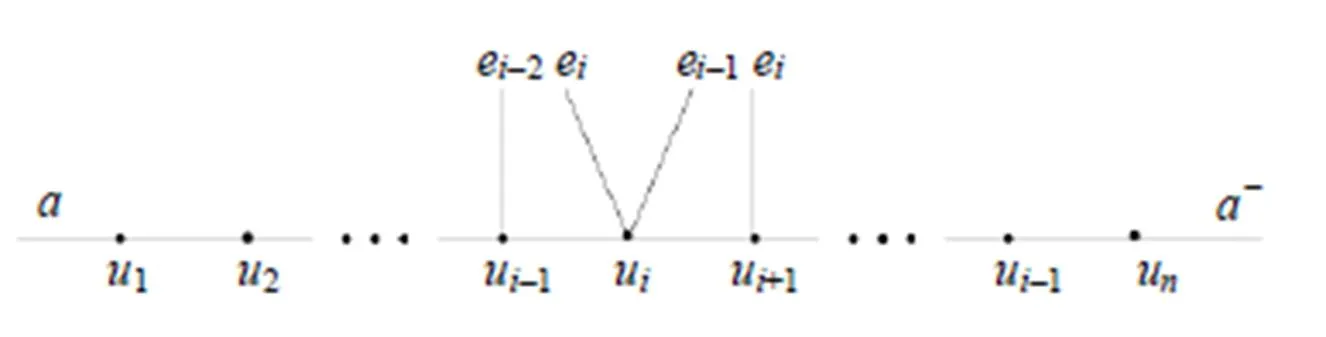
图3 由, 所构成的的子列
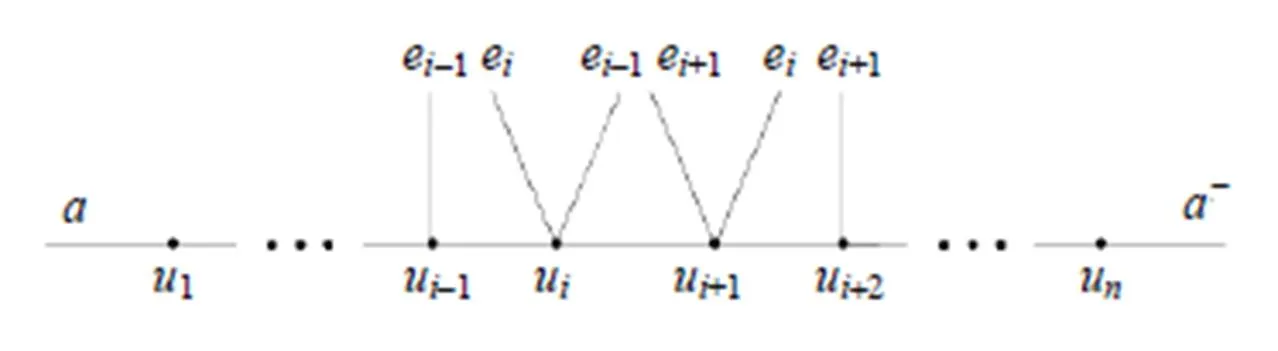
图4 由, , 让所构成的的子列
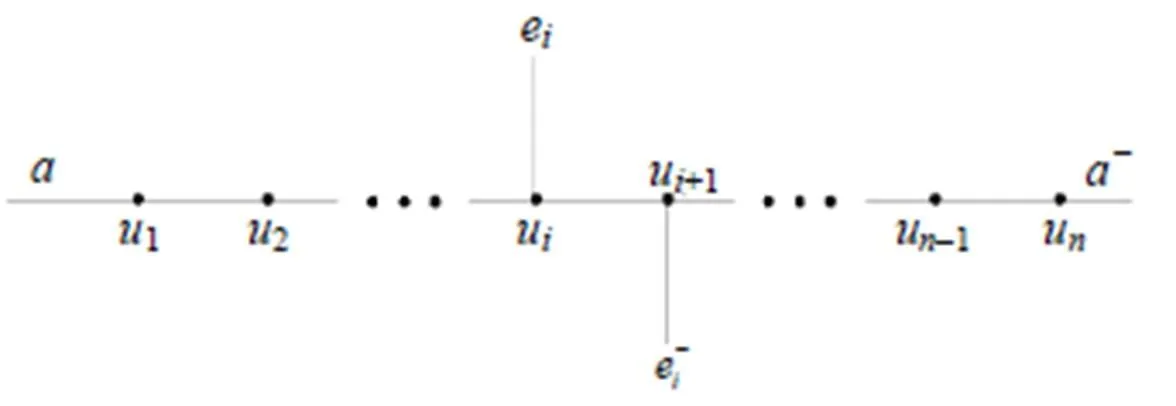
图5 由所构成的的子列
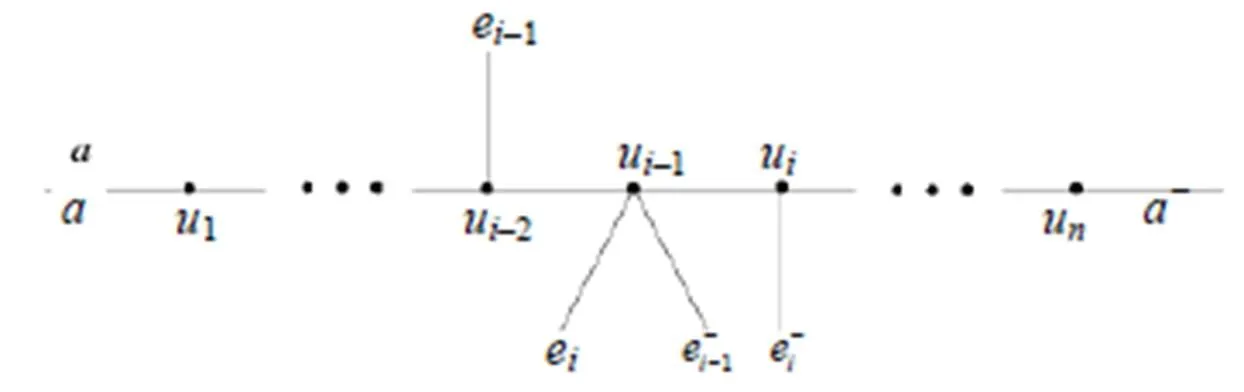
图6 由, 让所构成的的子列
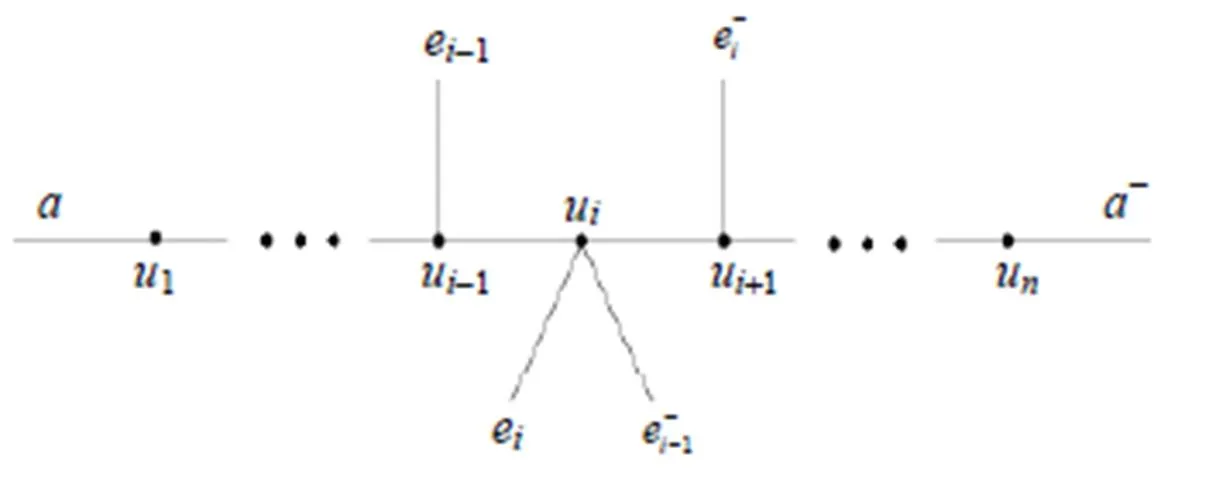
图7 由, 让所构成的的子列
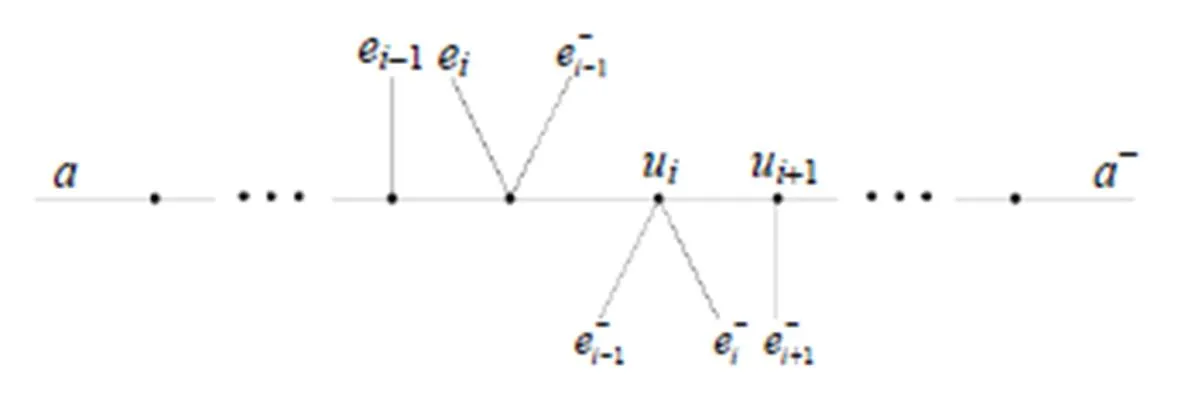
图8 由, ,和让所构成的的子列
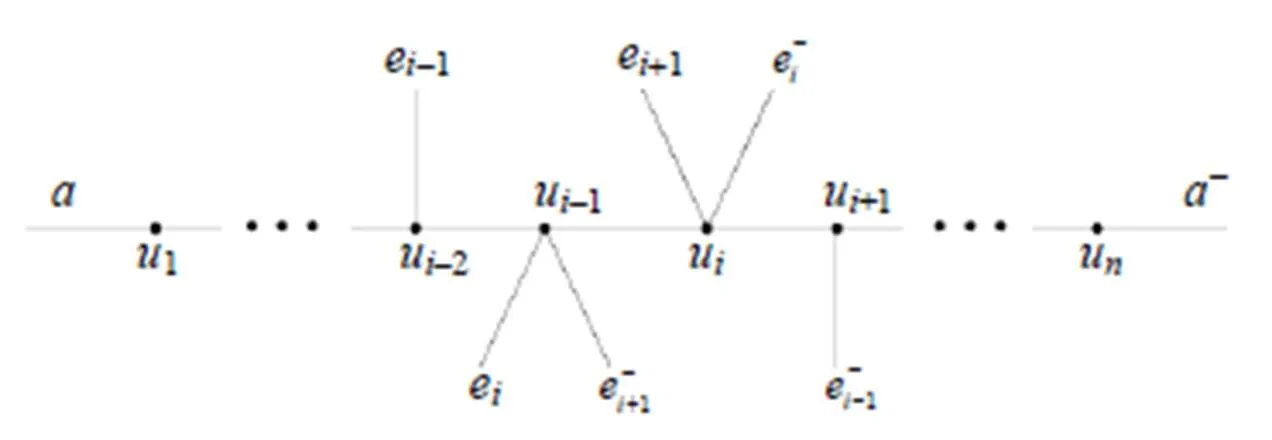
图9 由, ,和让所构成的的子列
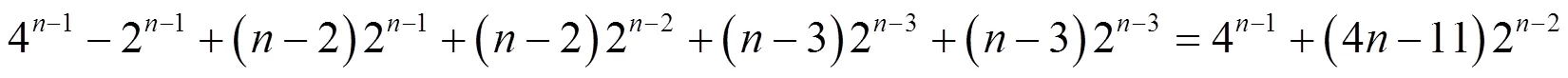
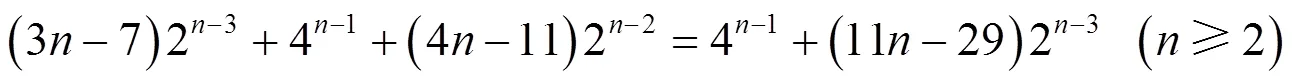
3 结束语
[1] GROSS J L, FURST M L. Hierarchy for imbedding-distribution invariants of a graph [J]. Graphy Theory, 1987, 11(2): 205—20.
[2] Furst M L, Gross J L, Statman R. Genus Distributions for Two Classes of Graphs [J]. J Combin Theory Ser B, 1989, 46: 22—36.
[3] Gross J L, Tucker T W. Topological Graph Theory [M]. Dover: Dover Publications, 1987.
[4] Gross J L, Robbins D P, Tucker T W. Genus Distributions for Bouquets of Circles [J]. J Combin Theory Ser B, 1989, 47: 292—306.
[5] Kwak J H, Lee J. Genus Polynomials of Dipoles [J]. Kyungpook Math J, 1993, 33: 115—125.
[6] Tesar E H. Genus Distribution of Ringel Ladders [J]. Discrete Math, 2000, 216: 235—252.
[7] Wan L X, Liu Y P. Orientable Embedding Genus Distributions for Certain Types of Graphs [J]. J Combin Theory Ser B, 2008, 98(1): 19—32.
[8] 杨艳, 郝荣霞. 扇图在曲面上嵌入的分类[J]. 应用数学学报, 2008, 31(5): 792—798.
[9] 朱子龙, 刘彦佩. 两类图的亏格分布[J]. 沈阳师范大学学报, 2006, 24(1): 1—5.
[10] 赵喜梅, 刘彦佩. 类圈图的亏格分布[J]. 数学物理学报, 2008, 28(4): 757—767.
[11] ChenJ, Gross J L, Rieper R G. Overlap matrics and total embedding distribution [J]. Discrete Math, 1994, 128(1—3): 73—94.
[12] 魏白, 黄元秋. 一类图在小亏格曲面上的嵌入[J]. 湖南师范大学自然科学学报, 2012, 35(5): 24—29.
Embedding on torus of a one type of Graph
LI WanSheng, HUANG YuanQiu, ZHANG XiangLin, LIU XinQiu
(Mathematics and Computer Science College, Hunan Normal University, Changsha 410081, China)
Genus; torus; joint tree
10.3969/j.issn.1672-6146.2014.03.001
O 157.5
1672-6146(2014)03-0001-06
email: liwansheng_lws@163.com.
2014-04-01
(责任编校:刘晓霞)
