同余格范畴中态射的性质

李 静

(泰山学院数学与统计学院，山东泰安 271021)

格可以作为一个偏序集来研究，也可以作为一个代数系统来研究，在格结构中引入同余关系，从而出现了同余格的概念，有关同余格的结论，可以参见文献［1－2］.本文研究了以同余格为对象，以保格同余关系的格同态为态射的同余格范畴，并得到了此范畴中的态射的有关结论.本文中所涉及的范畴概念，可参见文献［3］.

定义 1［1］设 θ是格 L 的一个等价关系，如果对任意的 ai，bi∈L(i=0，1)，由

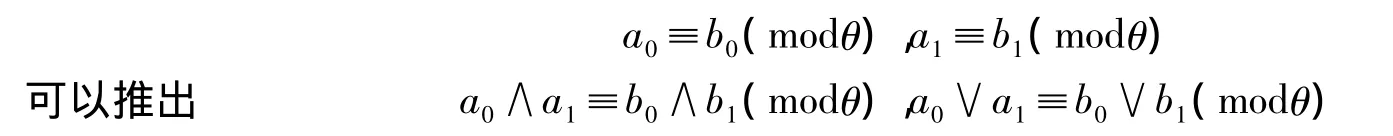
则称θ为L上的格同余关系，简称格同余.

注1 格L上的一个等价关系θ是L×L的子集，所以上述的定义也可叙述为:设θ是格L的一个等价关系，如果对任意的 ai，bi∈L(i=0，1)，由(a0，b0)∈θ，(a1，b1)∈θ，可以推出

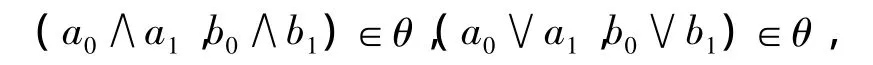
则称θ为L上的格同余关系.

把格L上的所有同余关系放在一起作成一个集合，记为ConL，在此集合上赋予偏序为集合的包含序，那么(ConL，⊆)作成一个偏序集.

定理1［1］若∀θ，φ∈ConL，θ∧φ =θ∩φ，且 x≡y(θ∨φ)当且仅当存在一个由 L中的元素成的序列z0=x∧y，z1，…，zn－1=x∨y，使得 z0≤z1≤…≤zn－1，且对任意的 i，0≤i≤n －1，有 zi≡zi+1(θ)或 zi≡zi+1(φ)，则ConL作成一个格.

定义2［1］格L上所有同余关系的集合赋予包含序作成的格称为同余格.

定理2［1］设任意格L，则ConL是分配的代数格.

本文中以同余格为对象，保格同余关系的格同态为态射的范畴，称为同余格范畴，记作CON.

命题1 仅含有恒等关系和全关系的同余格A到任意同余格B的态射是唯一的.

证明 因为同余格范畴中的态射f是保格同余关系的格同态，从而f是保序的，所以f将恒等关系映射为恒等关系，将全关系映射为全关系，即f是唯一存在的.

注2 由上述命题可知，同余格范畴中仅含恒等关系和全关系的同余格是始对象.例如，模格M3上的所有同余关系的集合ConM3，仅含恒等关系和全关系.

注3 当L为单元素格时，ConL也为单元素的同余格.

命题2 任意同余格到单元素的同余格的态射是唯一的.

注4 由上述命题可知，同余格范畴中含有一个同余关系(即此关系既为恒等关系又为全关系)的同余格是终对象.

命题3 同余格范畴中，任意同余格到单元素的同余格的态射是常值态射.

证明 由命题2知单元素的同余格是终对象，又由常值态射的定义知此命题显然成立.

定理3 在同余格范畴中，(i)任意两个态射有等化子;

(ii)任意两个态射有余等化子.

证明 (i)设f，g:A→B为任意的保格同余关系的格同态，其中A，B为同余格.令E={α∈A|f(α)=g(α)}则E为同余格.设i:E→A为含入映射，则i保格同余关系，所以i为CON态射，且显然有f◦i=g◦i.对于任意的保格同余关系的格同态 e':E'→A，使得 f◦e'=g ◦e'，即∀β∈E'，f◦e'(β)=g◦e'(β)，所以e'(β)∈E.定义:E'→E为∀β∈E'(β)=e'(β)，那么为保格同余关系的格同态，并且有e'=i◦.

综上，f，g 有等化子 i:E→A.

(ii)设 f，g:A→B 为CON －态射，其中 A，B 为同余格.取 θ为 B 上的包含 E={(f(α)，g(α))|α∈A}的最小同余关系，那么B/θ是一个格.故令同余格C=B/θ，且q:B→C为保格同余关系的格同态，故q为 CON －态射，且显然有 q◦f=q◦g.对于任意的 CON －态射 q':B→C'，使得 q'◦f=q'◦g，即∀α∈A，q'◦f=q'◦g，所以∀α∈A，(f(α)，g(α))∈θ.定义:C→C'为∀β∈B，(［β］)=q'(B)，其中［β］=q(B).那么为保格同余关系的格同态，并且有∀β∈B，q'(B)=(［β］)=(q(β))=◦q(B)，即q'=◦q.

综上，f，g有余等化子q:B→C.

注5 由定理3可知同余格范畴中任意同余格都有子对象和商对象.

［1］Gr¨atzer G.Congruence lattices［J］.Theoretical Computer Science，1999(217):279－289.

［2］Davey B.A.，Priestley H.A.Introduction to lattices and order［M］.London:Cambridge University press，1990.

［3］Herrlich H.Category theory［M］.Berlin:Heldermann Verlag，1979.