利用霍尔元件测量空心铜管的线膨胀系数

裴 娟，秦羽丰，孙振翠，贾景立

(1.山东交通学院理学院，山东济南 250023;2.山东农业大学信息与工程学院，山东 泰安 271018)

固体材料因温度变化，在一维方向上引起的长度变化称为线膨胀.表征线膨胀的物理参数是线膨胀系数，它是材料的基本物理参数之一.在桥梁、道路等工程设计中都要充分考虑材料的热膨胀特性.目前，实验室中测量金属线膨胀系数的最常见方法是光杠杆放大法［1］.虽然该方法简单易行，但是测量过程中需要直接测量的物理量较多，如光杠杆的臂长，光杠杆镜面到望远镜镜尺组的距离，以及因温度升高引起的标尺读数的增量等［2］，测量程序繁琐，降低了测量精度.为了减少物理量的测量个数、提高测量精度，我们基于霍尔元件测量微小位移的原理［3-5］，自主搭建了一套测量固体线膨胀系数的实验装置.利用该装置快速、准确地测出了空心铜管在一定温度范围内(20.6℃ -70.6℃)的线膨胀系数.

1 实验原理

1.1 固体的线膨胀系数［6］

设温度为t1时，物体的长度为L1;温度为t2时，该物体的长度为L2，当温度变化范围不大时，固体的伸长变化量ΔL与温度的变化量Δt及原长度L1成正比，即

其中，比例系数α称为线膨胀系数.所以

1.2 霍尔元件传感器原理

如图1所示，霍尔元件垂直置于磁感强度为B的磁场中(Z轴方向)，在其一组对边通以电流I(X轴方向)，则在与这二者垂直的方向上(Y轴方向)，即另外的一组对边之间将产生霍尔电势差UH，称为霍尔电压.

上式中KH为霍尔元件的灵敏度.

图1 霍尔效应原理图

将通有电流I的霍尔元件置于均匀梯度磁场中，当霍尔元件沿磁场方向(Z轴)发生位移的变化时，霍尔电压将发生变化，变化量为:

其中ΔZ为位移量

磁场沿Z轴方向的变化率.保持霍尔元件中的电流I不变，当霍尔元件在均匀梯度磁场(即为常数)中沿Z轴移动时，当位移量较小，即ΔZ〈2 mm时，霍尔电压的变化量ΔUH与位移量ΔZ之间存在良好的线性关系［5］

利用公式(4)，可以把长度量ΔZ的测量转化为电学量ΔUH的测量.这样只要确定公式(4)中的系数K0，就可以利用霍尔元件、电压表等直接测出公式(1)中的线膨胀系数α.

2 结果与讨论

2.1 测量系数K0

(1)我们利用毫伏电流表、毫伏电压表、直流稳压电源、读数显微镜、霍尔元件和自组装的均匀梯度磁场等搭建了一套确定系数K0的实验装置.如图2所示，将霍尔元件及其固定杆呈水平状态固定在读数显微镜的镜筒上，通过转动读数显微镜的微调手轮，使霍尔元件在均匀梯度磁场中沿Z轴方向上下移动.

其中，均匀梯度磁场是由两个完全相同的钕铁硼强磁铁(中心场强为0.15T，尺寸为60.0mm×40.0mm×5.0mm)同极(S极)相对放置组成，两磁铁之间的间距为12mm.磁铁正对面积(60mm×40mm)是霍尔元件面积(2.0mm×2.0mm)的600倍，并且霍尔元件垂直磁场放在该间隙的中心，所以在测量中可以忽略边缘效应带来的影响.由公式(4)可见，通过改变霍尔元件在磁场中的位置，测出相应ΔUH与位移量ΔZ，就可以确定系数K0.

(2)给霍尔元件一组对边输入工作电流10.00mA，转动读数显微镜的微调手轮，找到霍尔元件在均匀梯度磁场中的“零”位置，即数字电压表显示0.0 mV.记录此时读数显微镜的位置读数Z1和电压表的示数U1，沿着该方向继续转动读数显微镜的微调手轮，使霍尔元件在均匀梯度磁场中沿Z轴方向移动，每移动0.200 mm记录下相应的电压表示数U，共测量7个点.为了减小测量误差，我们又将霍尔元件沿相反方向移动，每移动0.200 mm，记录下相应的电压表示数U'，依次测量7个点.测量数据见表1.

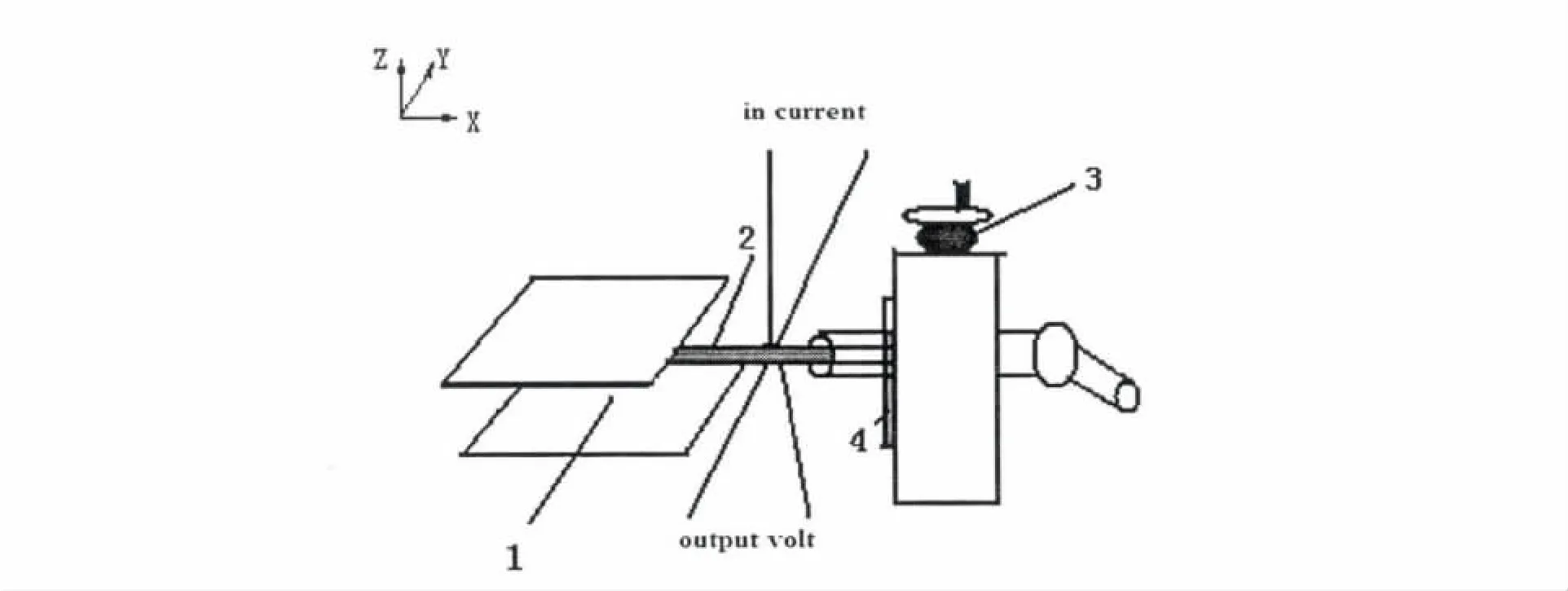
图2 实验装置图

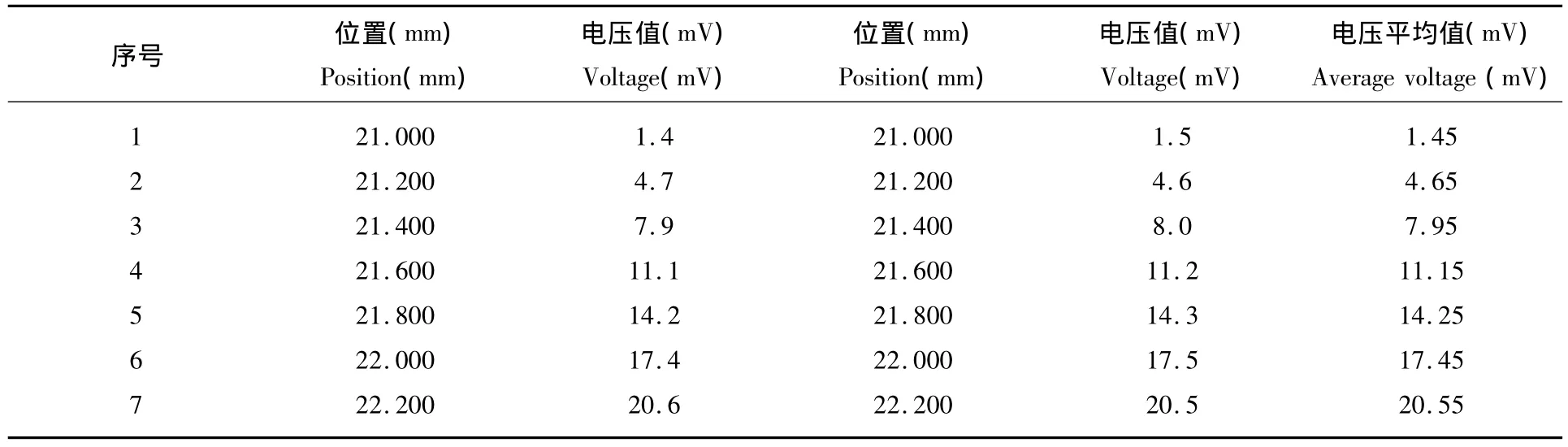
表1 室温20.6℃时读数显微镜位置Z和霍尔电压U

我们利用Origin数据处理软件对所测数据进行了线性拟合，如图3所示.作图时以电压U为纵坐标，读数显微镜的读数Z为横坐标.由图3可见，霍尔电压U与霍尔元件位移量Z之间存在良好的线性对应关系.通过线性拟合得到公式(4)中的系数K0:

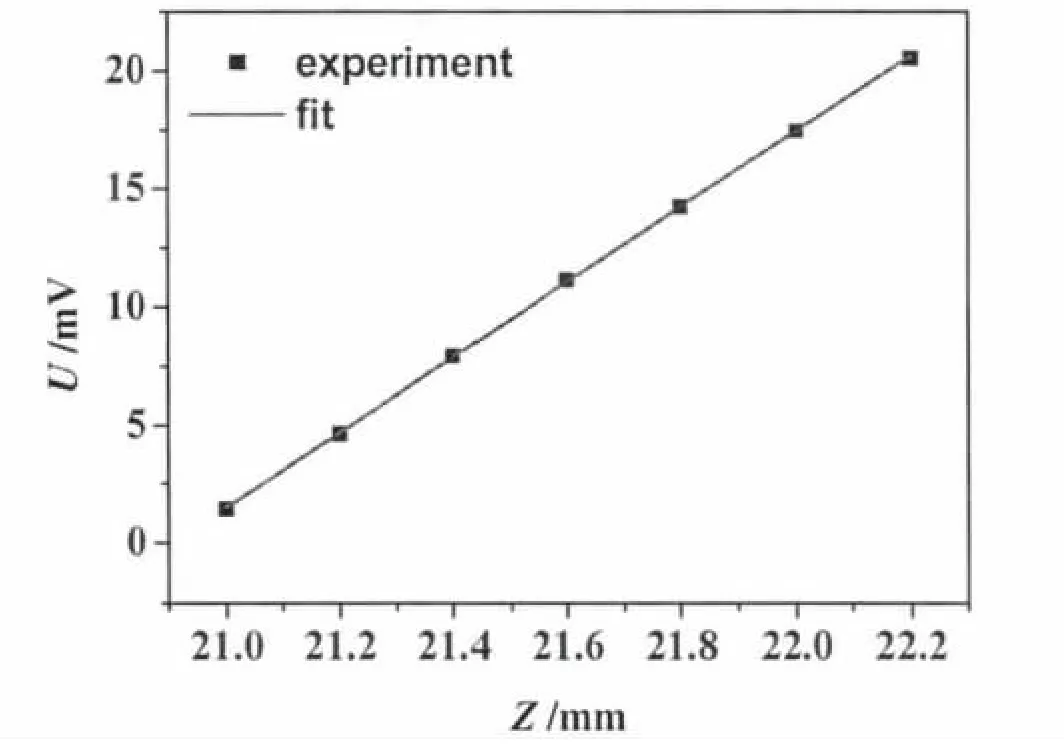
图3 U-Z线性关系图

2.2 测量空心铜管线膨胀系数α

用固体加热仪替换图2中的读数显微镜，将空心铜管放入固体加热仪中，空心铜管内插有记录温度变化的温度计，霍尔元件固定杆固定在铜管上.实验装置如图4所示.

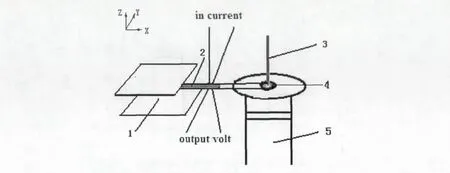
图4 实验装置图

将固体加热仪接通电源，内置铜管受热膨胀向上升起，带动霍尔元件及其固定杆在梯度磁场中发生位置的变化，即霍尔电压的变化.将室温20.6℃作为初始温度，记录此时电压值，然后温度每升高10℃，记录一次霍尔电压值U，直到升温至70℃，一共记录6个点.为了减小测量误差，我们也测量了降温过程中对应的电压值，具体测量数据见表2.

表2 不同温度下的霍尔电压U

我们用毫米尺测量了室温20.6℃下铜管的原长度L=502.0 mm.

为了丰富计算方法，此处，我们采用逐差法处理数据.首先将表2中电压值变化量的六个数据按顺序分成两组，第一组数据为U1、U2、U3、，第二组数据为U4、U5、U6、;然后采取对应项相减的办法，计算了温度在20.6℃ -70.6℃范围内，温度差为10℃的电压值ΔUH，即

铜管在一定温度范围内(20.6℃ -70.6℃)的线膨胀系数的理论值为1.67×10-5/℃.将我们的实验值与理论值作比较，得出相对误差

由此可见，实验值与理论值吻合的较好.

3 结论

基于霍尔元件测量微小位移的原理，我们成功地设计了一套测量金属线膨胀系数的实验装置.与光杠杆放大法测量相比，利用该装置进行实验，不仅减少了物理量的测量个数，而且提高了测量精度.表明该测量装置和测量方法具有重要的理论与实践价值.

［1］胡君辉，李丹，唐玉梅，等.光杠杆法测定金属线膨胀系数实验分析［J］.大学物理实验，2010，23(1):30-32.

［2］吴锋，张昱.大学物理实验教程(第1版)［M］.北京:科学出版社，2008.

［3］赵国明，李大磊.霍尔传感器在杨氏模量测量中的应用［J］.吉林化工学院学报，2010，27(2):74-76.

［4］张勇，徐杰，郭霞，等.利用霍尔位置传感器测杨氏模量［J］.大学物理实验，2010，23(3):39-41.

［5］金正宇，张迪儿，陆申龙.一个经典力学实验方法的改进——霍尔传感器测杨氏模量［J］.实验室研究与探索，2000(2):36-38.

［6］原所佳.物理实验教程(第3版)［M］.北京:国防工业出版社，2010.