混合高斯参数估计的两种EM算法比较

刘旺锁，王平波，顾雪峰



混合高斯参数估计的两种EM算法比较

刘旺锁1,2，王平波1，顾雪峰1

(1. 海军工程大学，湖北武汉 430033; 2. 广州大学，广东广州 510006)

混合高斯模型是一种典型的非高斯概率密度模型，获得广泛应用。其参数的优效估计可以通过最大似然方法获得，但最大似然估计往往因其非线性而难以实现，故期望最大化(Expectation-Maximization, EM)迭代算法成为一种常用的替代方法。常规EM算法性能受迭代初值设置影响大，且不能对模型阶数做出估计。一种名为贪婪EM的改进算法可以克服这两个缺点，获得更为准确的模型参数估计，但其运算量一般会远大于前者。本文对这两种EM算法进行综合研究，深入挖掘两者之间的关系，并基于相同的数值仿真实例，直观地演示比较两者的性能差异。

混合高斯；最大似然估计；期望最大化；贪婪期望最大化

0 引言

混合高斯(Gaussian Mixture, GM)模型是一种比较优秀的非高斯概率密度(Probability Density Function, PDF)模型，它具有参数少、结构简单、物理意义明显直观、拟合性能好等一系列优点，为雷达、声呐、通信、语音、图像等信号处理领域所广泛采用。使用GM模型对数据进行非高斯PDF建模的关键是如何快速、准确地得到GM模型参数估计。众所周知，对于非随机未知确定量，若其优效估计存在，则必然是最大似然估计(Maximum Likelihood Estimation, MLE)[1]。所以，首选是寻求GM参数的MLE。

但是，对于多参量同时估计问题，MLE一般难以严格实现。此时，往往代之以一种名为期望最大化(Expectation-Maximization, EM)的迭代算法[2]。文献[3]中提出了GM参数估计的EM迭代算法。这种EM算法存在参数初始化问题，如果初始化不恰当，迭代可能会错误地收敛于局部极值，不能得到正确的参数估计。不幸的是，对于GM参数估计，理想的EM迭代初始化方案尚未建立，这是EM算法应用的主要局限性所在。EM算法的第二个局限性是，它不能对GM模型阶数做出估计，只能在固定的GM阶数下进行。这就是说，使用EM算法，必须对GM模型阶数做出预先假定，而对于某些极端非高斯数据，实际中很难事先确定其GM阶数。

为了克服EM算法的这两个缺陷，文献[4]提出了一种名为贪婪EM(Greedy EM, GEM)迭代的改进算法(为以示区别，下文把传统EM算法简记为CEM)。理论上，GEM算法不依赖于初始值，且可自适应估计GM阶数。

文献[5]、[6]分别把CEM算法和GEM算法引入到了水声信号处理中。而且，文献[5]中提出了一种多初值初始化方案，可以部分地避免错误收敛问题。受当时数值仿真方法的限制，文献[6]直接使用一段海试数据简单演示了GEM算法的性能。本文将对CEM算法和GEM算法进行综合研究，深入发掘两者之间的关系，并基于相同的数值仿真实例，直观而详细地比较两者的性能差异。

1 混合高斯模型

一般地，GM模型的PDF可表述为如式(1)所示的加分布形式：

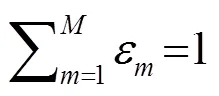
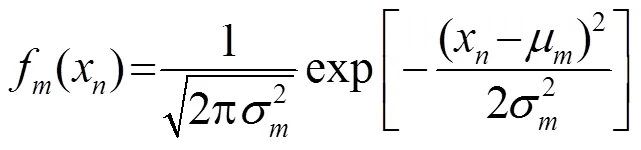
可以用图1所示的“完全数据”的概念来解释混合高斯数据的形成过程：

图1 完全数据形成图解

2 CEM算法

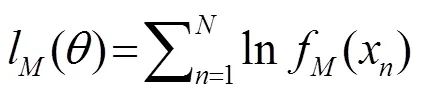
基于对图1所示完全数据概念的理解，Aaron[3]导出了GM参数MLE的CEM算法，省略中间步骤，主要迭代公式如(5)所示。

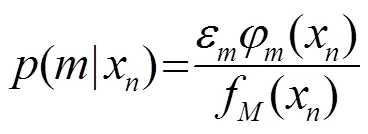
CEM迭代算法流程如图2所示。

可以看到，在假定模型阶数和初始化模型参数后，即可使用式(5)更新参数估计，直到满足令式(4)所示似然函数积分值取得最大。这就是CEM迭代算法的基本思想[3]。

在文献[5]中提出的多初值CEM方案如图3所示。依据图示方案实施估计，可以大大降低迭代收敛于局部极值点的错误概率。

3 GEM算法

GEM算法的理论依据是，一个混合分布的似然函数最大化过程可以通过一种所谓“贪婪”吸附的方式完成，即依据一定的规则，相继向混合分布中增加新的高斯成员，直至最终完成数据的PDF拟合任务。

图2 CEM估计算法流程图

图3 多初值的CEM算法

不难发现，不同于CEM算法在起始时即对GM所有可能源成份做出初始配置，GEM算法是从一阶最佳GM拟合(即一个最佳高斯源)开始的，其初始化是根据数据通过计算完成的。接下来，即重复如下两步，直到满足循环停止条件(比如达到了预定模型阶数)：

(1) 插入一个新的源成份；

(2) 应用EM迭代直到收敛。

有了初始化高斯参数和权系数，用式(8)对参量进行更新(此即partial EM迭代算法，简记为pEM)，选择使对数似然函数最大的一组参数作为新加入高斯分量的参数。

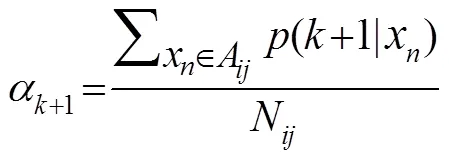
对给定的样本序列，上述思路的GM模型参数GEM估计算法流程如图4所示。

4 仿真实例

图4 GEM算法流程图

图5 数值仿真实例的波形和PDF

图6给出了根据这两种方法得到的参数估计绘制出的PDF曲线(分别标记为CEM、GEM)对比。为了便于比较，图中同时给出了理论PDF曲线和根据柱状图统计(这是一种常用的、适合于大样本量的分布统计分析方法：平分样本值域为若干连续区间，统计取值落于这些区间内的点数，以此可得到样本值的大致分布)得到的PDF曲线。于是，每幅图中共有4条PDF曲线。图6(a)中显示PDF原值，为了方便观察各条曲线的区别，图6(b)中给出了它们经过最大值归一化后的对比情形。

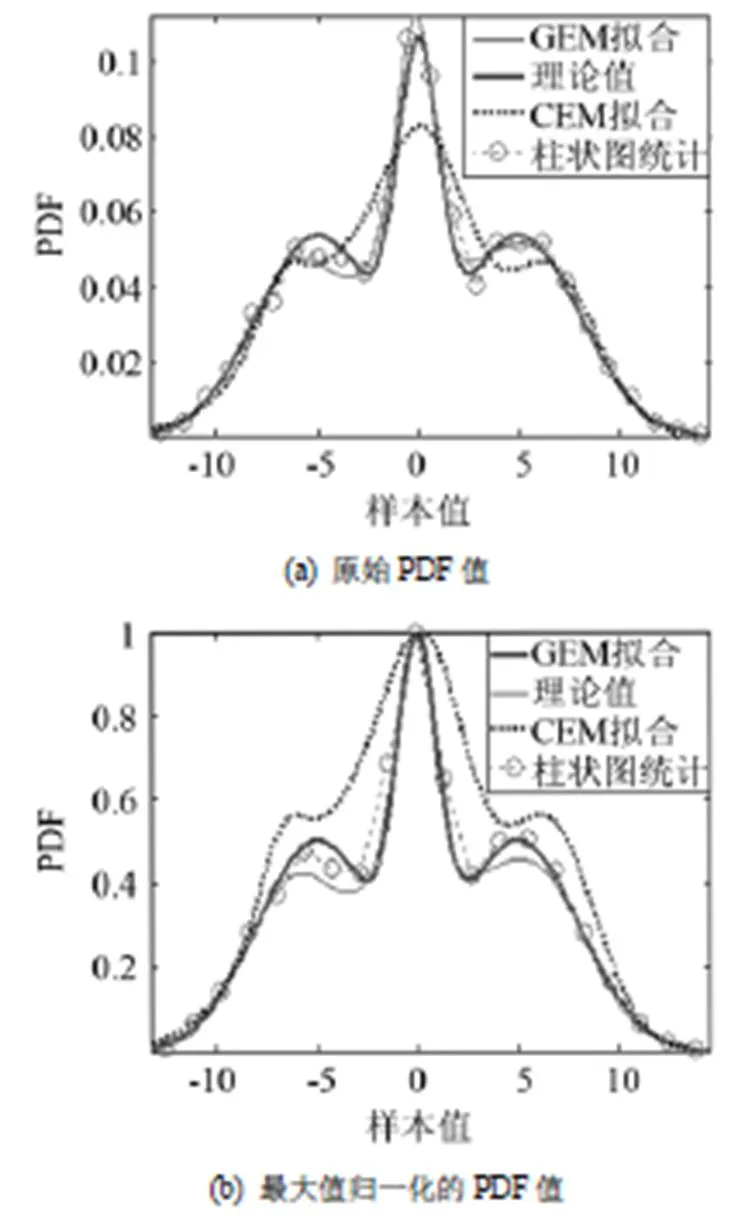
图6 PDF曲线比较

由图6可见，GEM算法得到的PDF曲线与理论PDF曲线重合程度远高于CEM算法，这说明前者PDF拟合性能明显优于后者。在本例这种样本量较为充足的条件下，GEM拟合与柱状图统计PDF拟合性能相当。

5 结语

GM模型是对数据进行非高斯PDF建模的有效模型之一。CEM算法是GM模型参数估计的常用方法，但CEM不能估计模型阶数，估计精度受初始值设置影响严重。而GEM算法则可以克服这些缺点，但运算量较大。

本文系统地梳理了CEM和GEM算法的关系及各自优缺点，并基于同一仿真实例对其性能进行了直观比较演示。比较结果表明：GEM算法可以取得优于CEM算法的PDF拟合性能，且能自动估计GM模型阶数。

由于通过不断新增高斯分量的方式逼近最大似然估计，所以GEM算法不受初值设置影响(即使最初的初值设置不合理，它也可以通过后续新增高斯分量的方式予以弥补)，可以取得较为稳定的估计性能。但是每一次新增高斯分量，都会相应增加运算量，所以GEM算法运算量往往远大于CEM算法。下一步将重点研究如何把GM阶数限定在一个较小范围内应用GEM算法对水声混响数据进行高效的PDF建模，并对CEM和GEM算法估计精度和速度等性能做出统计性比较，以最终判定究竟哪种方法更适用于水声混响数据的统计建模。

[1] Steven M Kay. Fundamentals of statistical signal processing: Estimation theory[M]. New Jersey, USA: Prentice Hall, 1998: 326.

[2] Redner R A, Walker H F. Mixture densities, maximum likelihood, and the EM algorithm[J]. SIAM Review, 1984, 26(2): 195-202.

[3] Aaron A D. Using EM to estimate a probability density with a mixture of Gaussians[DB/OL]. http://citeseer.ist.psu.edu, 2000.

[4] Verbeek J J, Vlassis N, Krose B. Efficient Greedy Learning of Gaussian Mixture Models[R]. Netherlands: Reports of Computer Science Institute of Amsterdam Univ, 2001: 153.

[5] 王平波, 蔡志明, 刘旺锁. 混合高斯概率密度模型参数的EM估计 [J]. 声学技术, 2007, 26(3): 498-502.

WANG Pingbo, CAI Zhiming, LIU Wangsuo. EM Estimation of PDF Parameters for Gaussian Mixture Processes[J]. Technical Acoustics, 2007, 26(3): 498-502.

[6] 卫红凯, 王平波, 蔡志明. 混响数据的混合高斯建模研究[J]. 声学技术, 2007, 26(3): 514-518.

WEI Hongkai, WANG Pingbo, CAI Zhiming. Study of reverberation for gaussian mixture model[J]. Technical Acoustics, 2007, 26(3): 514-518.

[7] 刘旺锁, 王平波, 顾雪峰, 等. 一种非白非高斯数据的数值仿真方法[J]. 声学技术, 2013, 32(3): 228-232.

LIU Wangsuo, WANG Pingbo, GU Xuefeng, et al. A simulation approach to colored non-Gaussian processes[J]. Technical Acoustics, 2013, 32(3): 228-232.

Comparison of two EM algorithms for Gaussian mixture parameter estimation

LIU Wang-suo1,2, WANG Ping-bo1, GU Xue-feng1

(1. Naval University of Engineering, Wuhan430033,Hubei,China;2. University of Guangzhou,Guangzhou510006,Guangdong, China)

Gaussian mixture is a typical and widely-used non-Gaussian probability density distribution model. The expectation-maximization algorithm is a usual iterative realization for the maximum likelihood estimation of its parameters. However, its performance depends highly on the initial values. And it can not estimate the order of Gaussian mixture. The greedy expectation-maximization algorithm can solve these problems by incrementally adding Gaussian components to the mixture. But its operation quantity is often much larger than the former. The relationship between these two algorithms is discussed, and their concrete realization methodsare given comparatively. With the same numerical instance, their performance differencesare illustratedand studied.

Gaussian mixture; Maximum Likelihood Estimation(MLE); Expectation-Maximization(EM); Greedy Expectation-Maximization(GEM)

TN911.7

A

1000-3630(2014)-06-0539-05

10.3969/j.issn1000-3630.2014.06.012

2014-04-29;

2014-08-07

国家自然科学基金资助项目(51109218)。

刘旺锁(1965－), 男, 江苏金坛人, 硕士生导师, 研究方向为声纳装备保障与效能评估、水声信号处理。

王平波, E-mail: blackberet@126.com