声速经验公式的适用范围分析

吴碧，陈长安，林龙



声速经验公式的适用范围分析

吴碧，陈长安，林龙

(中国人民解放军91388部队，广东湛江 524022)

声速经验公式是海水中温度、盐度和静压力的函数，通过对直接测量声速和间接测量声速的分析，并应用近年来收集的南海声速剖面仪SVP和CTD数据，对九种声速经验公式计算的声速与直接测量声速的差异进行了分析，得出了声速经验公式的计算差异范围，结果表明各个声速经验公式各有优势，不同的公式适用的范围也不一样，并给出了在不同的范围内应用何种声速经验公式能获得较高精度的结论。

声速剖面；声速经验公式；声速间接测量法；声速直接测量法

0 引言

多年来，海洋科学家们相继提出多种不同海水声速经验公式，不同的公式有着不同的时代背景和适用范围，一些公式尽管适用范围相同，但公式形式相差较大，推算结果也有差别，在不同的海域，由不同经验公式获得的声速差异较大，即使同一海域，由经验公式获得的声速同实际声速也会存在着较大的差异。目前对声速经验公式研究较多的是Chen-Miller、DelGrosso、Wilson三种算法，Christopher和watts[1]的声学研究结果表明，在海水中Del Grosso的声速算法要比Chen-Millero的好。陈红霞[2]等人的计算表明，用Wilson算法计算声速的速度要比用Chen-Millero算法计算声速的速度快。以上这些研究更多地侧重于算法的优劣，而很少涉及算法的应用。

海水声速对鱼雷、声呐等水下装备的影响很大，实际作战的水下探测设备，在不同的海区和深度，作战效果或许截然不同，这是由于不同海域和不同作战深度的声速变化造成的，通过对海水声速的精确测量，能够预先估算鱼雷的作用距离、声呐的探测距离等，对水下装备的作战、试验、科研等具有重要意义。用声速剖面仪测量的声速精度很高，但对于作战、试验这种大面积活动范围的情况下，测量效率较低，且设备昂贵，在实际应用中用温盐深剖面仪()测量海水的温度、盐度、压力，并通过声速经验公式进行计算得出声速。目前已有的多种声速经验公式对温度、盐度、压力的适应范围是不同的，大部分的文献都只是给出经验公式总的应用范围，本文在总结前人经验的基础上，通过对实测海洋环境数据的分析，研究各个声速经验公式在各种环境条件下的优劣性，为各个声速经验公式在不同的环境条件下的精确应用提供依据。

1 海水声速的测量

海水的声速可以通过声速剖面仪直接测量法和经验公式间接测量法两种方法求得。

1.1 直接测量法

直接测量法是利用声速仪(Sound Velocimeter Plus, SVP)直接测量声速[3]，以脉冲时间法为例，在所测水体介质中放置一组发射、接收换能器，它们之间的距离是精确的已知值，通过测量脉冲信号传播的时间，便可以计算出声速：

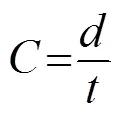
脉冲循环法是目前应用最广的声速测量方法，此类声速仪的精度一般可以达到每秒亚米级。

声速仪直接测定的海水声速虽然能比较客观地反映声波在特定水区、不同水层的传播特性，但设备贵重，参数单一，难以实现大面积的声速场的测量和预报。

1.2 间接测量法

间接测量法利用海水中的声速是温度、盐度和静压力的函数[4]，采用CTD测量海水的温度、盐度和压力随深度的变化，进而通过经验公式来计算声速。由于间接测量传感器体积小、操作简单、测量准确度高，并可以同时实现海水多参量高精度快速测量，有利于结合海洋学预报获得海洋声速场预报，因此间接测定海水声速在实际中得到了广泛的应用。从上世纪50年代开始，海洋科学家们相继提出不同海水声速经验公式，共有10种不同的声速经验公式，不同公式有不同的产生年代背景，有些公式还有相互联系。其中Del Grosso公式最早在1952年提出，几经修改于1974年确定。Wilson公式也叫Wilson精确公式，虽然提出年代早，但直至现在还被公认为较为稳定的公式；而Medwin公式其实是Wilson公式的简化。Chen-Millero-Li公式是Chen-Millero公式[5]的改进版本。各个公式复杂度不同，其中Wilson公式长达23项，其次是Del Grosso公式和chen-millero公式，最简洁的Medwin公式才6项，因公式较多且复杂，文中不一一列出。这些公式的适用范围如表1。

2 声速经验公式的比较

声速剖面仪测量的声速精度较高，在间接测量声速的比较中可作为真值，但在比较前须先讨论在声速测量和计算过程中引入的误差大小。Paroscientific[6]证实，压力传感器的绝对精确度在整个量程上是±0.015%，则对应于从海水表面到3000 m深度的这种传感器大约有0.5 m的误差。假设电导率传感器的绝对误差是0.0003 S/m，温度传感器的绝对误差为0.001℃，则声速计算公式中的这些误差肯定会导致计算声速的误差，这个误差不大于0.05 m/s[2]。CTD采用美国SEA-BIRD海鸟电子有限公司生产的SBE917温盐深剖面仪，该设备的测量精度为：温度精度0.001℃、电导率精度0.0003 S/m、压力精度0.0015% FS，则声速计算公式根据该设备测量的温盐深值计算出的声速误差会小于0.05 m/s。声速剖面仪采用加拿大应用微系统有限公司生产的一种直接测量声速仪SV Plus，该仪器直接测量声速的精度为±0.06 m/s，对应的测量深度为0~3000 m。

近年在南海某海域进行了几十个站点的声速剖面测量，在时间上覆盖了4个(包括春、夏、秋和冬季)不同的季节。采用声速剖面仪(SVP)和CTD同步进行，以得到时间上和空间上较为一致的直接测量声速数据和水文数据，测量海深大于1500 m。将水文数据代入表1所涉及的经验公式，计算得到对应不同经验公式的间接测量声速数据。将几十个站位测量同一深度上的直接测量声速和间接测量声速分别进行算术平均，得到直接测量声速平均值C和间接测量声速平均值C(=1…..9，分别代表九种经验公式)，通过平均，偶然误差可被消除而且不会丧失任何典型特征。将两种平均值相减，得到间接测量声速与直接测量声速的差异值，如图1所示。

表1 声速经验公式概要

图1 声速差异图

3 结果分析

图1的纵轴为海区深度，横轴为间接测量声速与直接测量声速的差异值，从图中可以看出，9种算法的差异值随着深度的变化各有不同，以计算误差和仪器的测量误差均不大于0.06 m/s为参考依据，9种算法的结果均比计算误差和测量误差要大一个数量级。其中Wilson、Frye and Pugh、Leroy三种算法的趋势基本一致，均是随着海深的增大，差异值逐渐变大，Wilson的差异值范围为-0.16~0.425，Frye and Pugh的范围为-0.118~0.444，Leroy的范围为-0.023~0.405，Wilson的算法结果在60 m深处达到最小值，Leroy的算法结果在6 m深处达到最小值，Frye and Pugh的算法结果在80 m深处达到最小值，量级均小于计算误差和测量误差；Del Grosso、Coppens、Mackenzie、Lovett四种算法的趋势基本一致，Del Grosso的差异值范围为-0.616~-0.114，Coppens的差异值范围为-0.628~-0.023，Mackenzie的范围为-0.675~-0.14，Lovett的范围为-0.628~-0.01，这四种算法均随着海深的增大，差异值逐渐变小，其中Lovett和Coppens在1300 m以深差异值量级均小于计算误差和测量误差；Chen-Millero算法的差异值跨度最大，范围为-0.561~0.32，在720 m左右达到最小值；Medwin算法的差异值与其他算法不一样，在0~380 m范围内其差异值与Del Grosso算法趋势一致，误差范围为-0.603~-0.292，但随着深度的增加，差异值逐渐增大，达到了-0.7。

由以上的分析可得出以下的结论：要得到精度较高的测量声速，经验公式的选择很重要，应根据不同的情况选择不同的经验公式，具体原则如下：

(1) 在南海地区使用Frye and Pugh 、Lovett 、Mackenzie和 Wilson公式时要注意海水的温度，因为南海海区夏季表层温度有时可高于30℃。而Del Grosso、Medwin、Chen-Millero 和Lovett适用的温度不低于0℃，不适用于我国渤海冬季冰冻层下面水层。

(2) Wilson、Medwin、Coppens、Chen-Millero-Li公式在淡水和海水中通用，Chen-Millero公式能适用于河口海岸冲淡水，其余公式仅适用于海水，其中Frye and Pugh公式盐度适用范围最小。

(3) 在浅海的声速测量中，适合使用Wilson、Frye and Pugh、Leroy三种经验公式进行声速的计算，在浅海中，这三种经验公式的精度很高，在某一深度上差异值小于计算误差和测量误差，而其他经验公式的差异值均超过0.4 m/s。在海表面，由于阳光、风等的作用，海水的温度较深海高，测量的数据表明60 m以浅的海水温度平均值大于24℃，夏季时更高，因此以上的三种经验公式在海水中更适合于高温低压的环境，但要满足(1)、(2)的条件；

(4) 虽然Wilson、Frye and Pugh、Leroy三种经验公式适用于浅海，但在不同的深度上其差异值也有区别，从择优选择的角度看，20 m以浅的深度上Leroy公式适用，20~100 m的范围内，Frye and Pugh公式适用，30~80 m的范围内，Wilson公式适用，在这三个范围内三种经验公式的差异值均小于计算误差和测量误差；

(5) 在大于100 m的深度上，Wilson和Leroy公式的差异值增长迅速，大于0.3 m/s，而Frye and Pugh公式的差异值虽然也在增加，但增速缓慢，在100~350 m深度内的差异值范围为0.05~0.2 m/s，相对于其他公式的差异值大于0.3、0.4 m/s的情况，在100~350 m深度上，Frye and Pugh公式是最优的选择；

(6) Del Grosso、Coppens、Mackenzie、Lovett、Chen-Millero、Medwin几种经验公式的差异值随着深度的增大而减小，从图1可看出，Chen-Millero公式的差异值跨度最大，先是随着深度逐渐变小，达到最小值后又逐渐增大，在650~850 m的深度上差异值小于计算误差和测量误差，而在350~1000 m的深度上，差异值范围为-0.2~0.13，是所有公式中差异值最小的，因此在350~1000 m的深度上最适合应用Chen-Millero公式；

(7) 在1000 m以深的深度上，Del Grosso、Coppens、Mackenzie、Lovett四种公式的差异值均小于0.2 m/s，而其他公式的差异值均大于0.2 m/s，因此在大于1000 m的深度上应用这四种公式是可行的，其中Lovett公式的精度最高，其次是Coppens公式、Del Grosso公式、Mackenzie公式。测量的数据表明：海水温度随着深度逐渐变小，在1000 m以深时小于5℃，也就是说以上四种公式更适合于高压低温的环境；

(8) Medwin公式的差异值在375 m左右达到最小值0.29 m/s，但在小于和大于375 m的深度上差异值逐渐增大，因此与其他的公式相比，Medwin公式最不适用。

4 结语

海洋声速是海上军事活动最重要的参数，声速测量精度在很大程度上影响着军事活动的策划、方案、行动等，快速获取海域范围内的声速是开展各种军事活动的基础。由于计算声速的经验公式较多，究竟应用哪种公式能计算得到较高精度的声速是目前面临的问题。本论文通过对各种经验公式的计算结果与实测声速的对比，获得了各种经验公式的计算误差，通过对计算误差的分析，得到这些经验公式在各种情况下适用范围的结论，能够为海上的作战、试验、科研活动提供依据。

[1] Christopher S M, Watts D R. Further evidence that the sound-speed algorithm of DeI Grosso is more accurate than that of Chen and Millo[J]. J Acoust Soc Am, 1997, 102: 2058-2062.

[2] 陈红霞, 吕连港, 华锋, 等. 三种常用声速算法的比较[J]. 海洋科学进展, 2005, 23(3): 359-362.

CHEN Hongxia, LU Liangang, HUA Feng, et al. Comparison between three commonly used algorithms of sound speed[J]. Advances in Marine Science, 2005, 23(3): 359-362.

[3] 关致和, 赵先龙, 于政, 等. HY1200声速剖面仪计算测深声速改正数方法[J]. 海洋测绘, 2006, 26(1): 66-68.

GUAN Zhihe, ZHAO Xianlong, YU Zheng, et al. Correction method of sound velocity Calculating by HY1200 SVP[J]. Hydrographic Surveying and Charting, 2006, 26(1): 66-68.

[4] 刘伯胜, 雷家煜. 水声学原理[M]. 哈尔滨工程大学出版社, 2002.

LIU Bosheng, LEI Jiayu. Principle of underwater acoustics[M]. Harbin: Press of Harbin Engineering University, 2002.

[5] Millero F J, Xu Li. Comments on ‘On equations for the speed of sound in seawater[J]. J. Acoust. Soc. Am., 1994, 95(5): 2757-2759.

[6] SBE. 911plus CTD System Operating and Repair Manual[M]. Bellevue, USA: Sea-Bird Electronics Inc., 2002.

Analysis of applicable scope of empirical equation for sound velocity

WU Bi, CHEN Chang-an, LIN Long

(Unit 91388,PLA, Zhanjiang 524022,Guangdong,China)

Empirical equation for sound velocity is the function of temperature, salinity and static pressure in sea water. After analyzing the sound velocity by direct measurement and indirect measurement, and utilizing the data collected by profiler SVP and CTD in South China Sea in recent years, the differences between the sound velocities calculated by nine kinds of empirical equations and the one with direct measurement are studied. The different scopes calculated by empirical equations for sound velocity are obtained. The result shows every empirical equation of sound velocity has its own advantage and their applicable scopes also differ. The conclusion is provided for using an appropriate empirical equation for sound velocity in actual situation to get higher accuracy.

sound velocity profile; empirical equation for sound velocity; indirect measurement method of sound velocity; direct measurement method of sound velocity

P733.2

A

1000-3630(2014)-06-0504-04

10.3969/j.issn1000-3630.2014.06.005

2013-10-10;

2014-01-15

吴碧(1974－), 女, 广东湛江人, 硕士研究生, 研究方向为仿真试验技术。

吴碧, E-mail: wubiwqbj@163.com