多体航天器姿态机动的终端滑模复合控制方法研究*

黎 飞，雷拥军，2

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

0 引言

根据航天器执行任务的需要，现代航天器通常带有对地遥感相机、扫描天线、多自由度机械臂等转动附件.这些附件运动规律复杂，往往不能事先确知，对于质量较大的附件，其大角度跟踪指向时对整星的惯量矩阵有较大的影响，使航天器呈现变参数、不确定性、非线性强耦合等控制对象特性，容易造成本体姿态产生较大的偏差;航天器本体大角度机动对附件的精确指向也较突出，甚至导致附件丢失跟踪目标.因此，在本体姿态运动控制中必须考虑附件运动的影响以及两者之间的耦合作用，而附件的指向控制也必须考虑本体姿态的变化，对平台和附件需要统一进行设计，即航天器姿态复合控制［1］.

日本学者［2］基于角动量守恒定律，为抑制天线(或机械臂)运动带来的姿态扰动，对航天器本体采用自适应前馈控制方法，在轨测试取得较好的控制效果.文献［3］和［4］将两刚体航天器作为单一被控对象考虑，分别采用自适应鲁棒控制和终端滑模控制方法设计控制器，这种控制策略使得控制器的维数随着附件数量的增加而增加，给计算机运算造成较大负担，不利于工程实现.文献［5］将天线运动信息作为前馈信号设计了“前馈+变结构”控制方案，同时用本体姿态偏差调整天线转角，若天线运动信息丢失，这种前馈策略容易造成系统不稳定.文献［6-7］采用改进的矢量力学方法建立了完整的两(三)刚体系统动力学模型，详细讨论了平台与附件之间的耦合作用，在忽略二阶小量和本体参考点运动的情况下，针对简化模型设计了卫星本体的“PID+前馈”控制器，然而这种简化处理不适用于平台与附件的大角度机动.

本文在完整两刚体动力学模型的基础上对系统特性进行分析，设计了满足本体与附件同时机动要求的复合控制系统.针对标称本体动力学模型，将有限时间干扰观测器与终端滑模控制方法结合起来，设计了适合本体大角度机动的姿态控制器.为减小本体机动对附件指向的影响，在附件控制器中引入对本体角加速度的近似补偿，并从运动学上对附件的指向角进行修正.

1 系统模型及问题描述

本文对机动能力较强的一类多体航天器进行研究，这类航天器太阳帆板尺寸较小，一般采用加强筋进行固定，因此帆板挠性作用不明显，可以将帆板的惯性特征与航天器本体合在一起考虑，如图1所示.

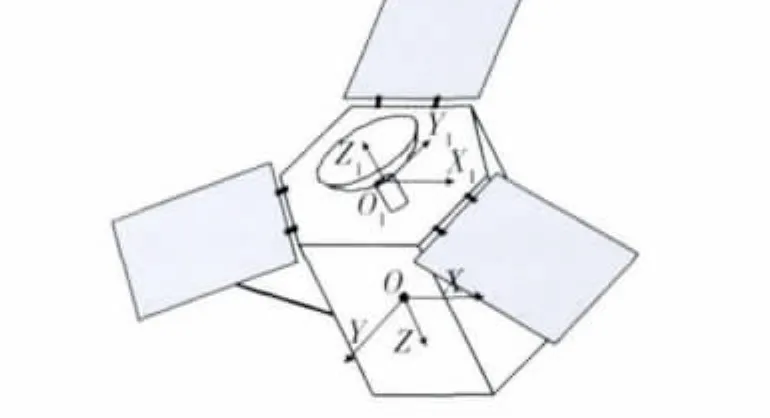
图1 两刚体航天器构型Fig.1 Configuration of the two-coupled rigid spacecraft

假设附件具有两轴转动能力，取附件坐标系原点为其在本体上的安装点O1，以附件未转动时的整星质心O为本体坐标系原点，采用Euler-Newton力学方法建立如下的完整两刚体动力学模型:

式中，M(φ)为系统广义惯量矩阵，φ=［φxφy］T为附件两轴转角，X=［ωT］T为本体及附件的角速度变量，N为X和φ的复杂非线性函数(具体描述见附录)，Tc=［uT］T为本体和附件的控制力矩，Td为环境干扰力矩.M(φ)的具体表达式为

式中，m=m0+m1为系统总质量，m0和m1分别为本体和附件的质量，J为整星惯量矩阵，J0和J1分别为本体和附件相对各自坐标系原点的惯量矩阵，J01为本体和附件的混合惯量矩阵，ρ为附件转动过程中系统质心在本体系的坐标列阵(附件处于标称位置时ρ=0，［·］×表示叉乘)，ρ1为附件质心在附件系的坐标列阵.规定附件先绕X轴转动，再绕Y轴转动，转动角度依次为φx，φy，则附件系到本体系的姿态转换矩阵C01为

为避免欧拉角、Rodrigues参数等姿态运动描述方法存在的奇异情况，选取没有奇点并且适合大角度姿态机动的四元数q来描述航天器姿态运动，即.为方便后面的推导，定义以下函数:

不考虑轨道运动，本体姿态运动学方程和附件转动运动学方程分别为

其中

由式(1)，(5)和(6)构成两刚体航天器系统的完整数学模型.可以看出，系统模型相当复杂，呈现高度非线性、强耦合和变参数的特性.随着附件质量、惯量增大，本体与附件之间的动力学耦合作用也会增强.特别指出，C01为附件转角φ的三角函数矩阵，在附件转动时是时变的，J、J01和ρ均包含C01，因此系统广义惯量矩阵M(φ)也是时变的，表现为附件转角φ的高阶非线性函数.

本文的控制任务在于设计一个鲁棒性较强的控制系统，使得本体姿态四元数跟踪目标四元数，附件指向被跟踪目标，即q→qd，φ→φd.

对多体航天器进行控制，若将多体动力学对象作为一个整体进行处理，控制器的维数会变得很高，对计算机造成较大的负担，不同的附件其执行机构特性不同，难以进行统一处理.因此，本文对本体与附件分别设计控制器，同时考虑两者之间的耦合作用.

2 本体姿态控制器设计

2.1 本体标称动力学方程

首先从系统中分离出适合于控制器设计的本体平台，以附件尚未机动时的系统惯量作为本体的标称惯量，将附件角加速度项、以及本体与附件的角速度耦合项作为附件对本体的干扰.

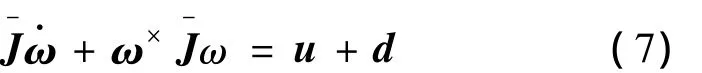
其中未被写入方程左边的各项均包含在d中.

在对目标姿态进行跟踪机动时，一般已知目标四元数qd和期望角速度ωd，其表达式为

令误差四元数为qe=［qevqe4］=FT(qd)q，经过坐标变换，姿态跟踪问题变为姿态稳定问题［8］.

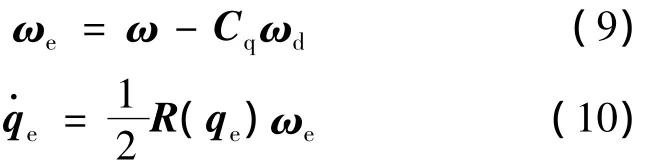
对式(9)求导，并代入式(7)中，得到

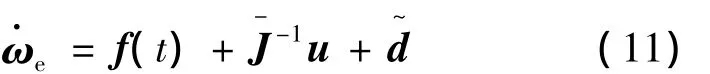
式中，f(t)为确定项为未知总扰动项，包括惯量不确定性、本体与附件的耦合作用、以及未知外界干扰等.假设，为保证闭环系统的稳定性，一般在控制律设计中取较大的Δd值，这在一定程度上增大了控制系统的保守性，因此有必要设计干扰观测器估计，然后在控制器中进行主动补偿.

2.2 有限时间干扰观测器

定义1.令x∈Rn，α＞0，sig(x)α函数定义为

其中，sgn(·)为符号函数.

本文利用文献［9］提出的鲁棒精确微分器来构造一种新的有限时间干扰观测器，具体表达式为

上述干扰观测器由两个鲁棒精确微分器组成，构造思路为:在没有测量噪声的情况下，第一个微分器的变量经过有限时间后;令z2为总干扰的观测值，得到观测误差e2的表达式，通过第二个微分器可在有限时间内得到

2.3 终端滑模控制器

引理 1［10］.对任意p∈ (0，1)，x ∈ R3，有如下不等式成立:

其中，λi，βi＞0，i=1，2 .

引理2［10］.令 τ1，τ2＞0，0＜α＜1，若Lyapunov正定函数V(x)满足V·(x)+ τ1V(x)+ τ2Vα(x)≤0，则系统是有限时间稳定的，稳定时间可由下式估计:

式中x0为t=0时刻的x值.

针对式(11)，选取如下快速终端滑模面［10］:

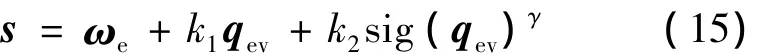
式中，s∈R3分别表示三轴的滑模变量，且k1，k2＞0，0＜γ＜1.令 τ1，τ2＞0，0＜α＜1，趋近律选为

定理1.对于存在外部干扰和惯量不确定性的航天器姿态控制系统，选择滑模面(15)和趋近律(16)，快速终端滑模控制器

能使误差四元数qev和角速度误差ωe在有限时间内收敛到0.

证明.对本定理的证明分为两步:第一步，证明系统轨迹能在有限时间内收敛到滑模面，即s=0;第二步，证明系统状态沿着滑模面在有限时间内收敛到系统原点.

(1)考虑 Lyapunov函数V1=0.5sTs，对V1求导，并代入控制律(17)，得到

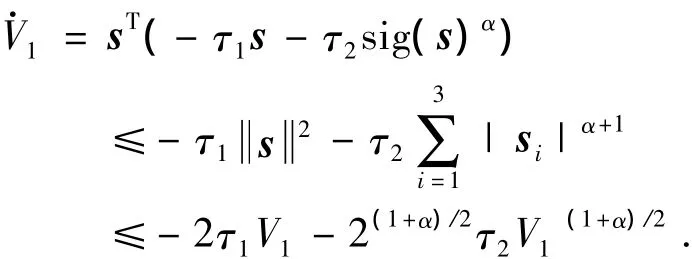
由引理2可得，系统(11)的轨迹会在有限时间t1内到达滑模面s=0.

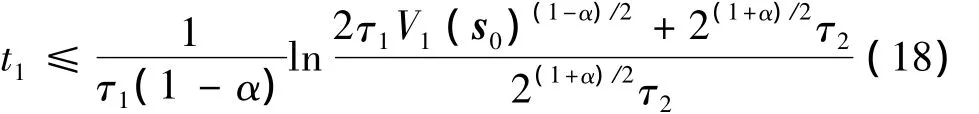
其中，s0为滑模面s在t=0时刻的初始值.

(2)若滑模面s=0，选取正定函数

由文献［10］的证明得到

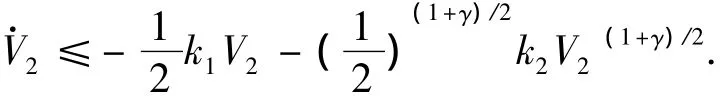
同样，由引理2知，系统轨迹沿着滑模面在有限时间t2内收敛到0，记总的收敛时间为T=t1+t2，则有

从而定理1得证.

3 附件指向控制器设计

3.1 附件运动学补偿

本体姿态机动过程中，对同一指向角，附件所需转角也会不同.从运动学上看［7］，附件转角相对于本体坐标系描述，而指向目标的轨迹通常以轨道坐标系描述，所以附件转角需要引入本体姿态的修正.

假设目标方位与轨道坐标系的OXoYo平面夹角为φp1，在OXoYo平面内的投影与OXo轴的夹角为φp2，则目标方位在轨道坐标系的分量为

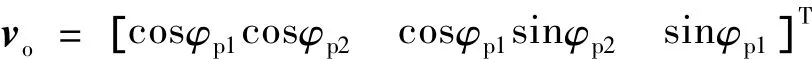
令Cbo为轨道坐标系到本体坐标系的转换矩阵，已知附件指向轴坐标为va=［0 0 1］T，则vo在本体系的分量可表示为

于是解得附件的参考转角φd为

3.2 “PID+前馈”控制器

从动力学上看，本体姿态角加速度与附件角加速度相互耦合，为减小姿态角加速度对附件的指向偏差，可在附件动力学方程中对其进行近似补偿.为方便设计附件控制器，将其转动动力学方程与运动学方程合并.对式(6)求导，得到

4 仿真验证

为验证论文提出的控制方法的控制效果，选用文献［7］描述的航天器本体模型和前向天线参数进行仿真.要求本体姿态对某一活动目标跟踪机动，附件对某一固定目标进行精确指向.

令航天器本体初始姿态角为［-10° 30°20°］T，按照3-2-1转序，初始姿态四元数为q(0)=［-0.127 7 0.239 3 0.189 3 0.943 7］T初始目标四元数为qd(0)=［0 0 0 1］T，期望的姿态角速度为

仿真步长选为h=0.02s，干扰观测器参数选为 β1=5，β2=2，λ1=2.5，λ2=0.5.

本体姿态控制器及附件PID控制器参数设置为k1=k2=0.8;τ1=τ2=0.2;γ=0.8;α=0.5;kp1=100，ki1=50，kd1=50.

仿真结果如图2～6所示.

图2 姿态四元数跟踪误差曲线Fig.2 Attitude quaternion tracking errors

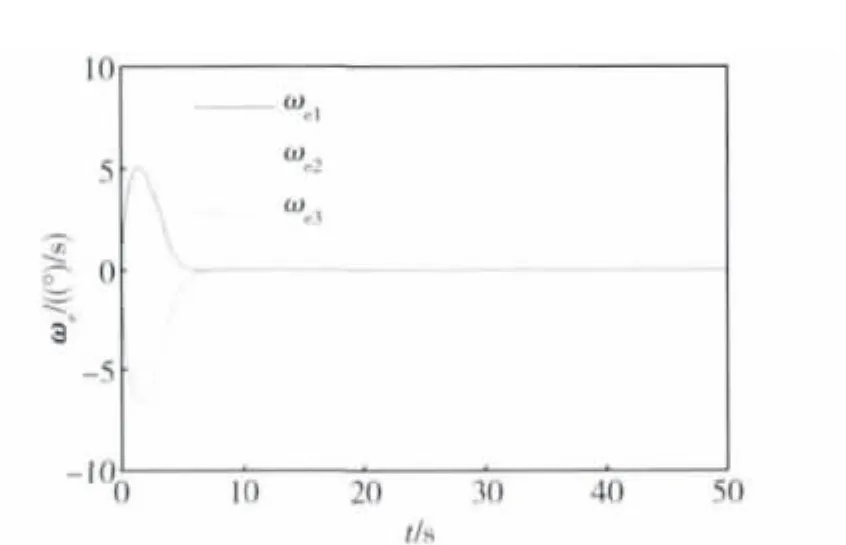
图3 角速度跟踪误差曲线Fig.3 Angular velocity tracking errors

由于对目标姿态设置了较大的期望角速度，本体姿态实际为大角度跟踪机动，为保证附件指向轴对给定目标的精确指向，附件也需要进行大角度的转动控制，从而对系统的惯量矩阵造成较强的影响.从图2～4可以看出，本体姿态能够快速跟踪给定的目标姿态，说明本体终端滑模控制器跟踪精度较高，鲁棒性较强.

附件在初始时刻，转角偏差较大，采用指令预处理器规划后，过渡过程变得比较平稳.由于在PID控制器中，对本体的角加速度进行近似补偿，附件在机动阶段以及稳定阶段的误差均有明显减少，指向精度在给定PID参数的情况下能够达到0.01°的水平.

图4 滑模面曲线Fig.4 Sliding mode surface

图5 附件参考转角及实际转角曲线Fig.5 Reference rotation angles of appendages and its actualrotation angles

图6 附件转角跟踪误差曲线Fig.6 Rotation angle tracking errors of appendages

5 结论

本文研究了航天器本体与附件同时机动跟踪这一控制问题，在完整两刚体动力学模型的基础上对系统特性进行分析，指出附件运动对整个系统的惯量特性影响较大，使系统呈现出变参数、强耦合以及非线性的特性.为便于工程实现，对本体与附件分别设计控制器，并在控制器之间考虑两者的耦合作用.该方法不需要精确知道附件运动对航天器动力学的影响，也不需要对系统动力学模型进行线性化处理，通过直接对非线性系统设计控制器，可以达到比较理想的控制效果.通过仿真表明，所设计的控制器具有良好的鲁棒性，控制精度较高，算法简单，具有较强的工程实用性.

［1］齐春子，吕振铎.挠性卫星天线跟踪指向系统的复合控制研究［J］.中国空间科学技术，1999，19(2):1-7.QI C Z，LV Z D.A study of compound control in tracking and pointing system of flexible antenna on satellite［J］.Chinese Space Science and Technology，1999，19(2):1-7.

［2］Yamada K，Yoshikawa S.Adaptive attitude control for an artificial satellite with mobile bodies［J］.Journal of Guidance Control and Dynamics，1996，19(4):948-953.

［3］袁长清，李俊峰，张威泰，等.航天器编队飞行多目标姿态跟踪终端滑模控制［J］.空间控制技术与应用，2010，36(5):18-24.YUAN C Q，LI J F，ZHANG W T，et al.Terminal sliding mode control for multi-target attitude tracking in spacecraft formation flight［J］.Aerospace Control and Application，2010，36(5):18-24.

［4］YUAN C Q，LI J F，WANG T S，et al.Robust attitude control for rapid multi-target tracking in spacecraft formation flying［J］.Applied Mathematics and Mechanics(English Edition)，2008，29(2):185-198.

［5］刘莹莹，周军.挠性卫星多轴指向复合控制方案研究［J］.系统仿真学报，2007，19(14):3286-3289.LIU Y Y，ZHOU J.Compound control for multi-axis pointing of flexible satellites［J］.Journal of System Simulation，2007，19(14):3286-3289.

［6］苟兴宇，李铁寿.一类附件有大角度跟踪机动卫星的动力学建模与控制［J］.动力学与控制学报，2004，2(2):29-32.GOU X Y，LI T S.Dynamical modeling and control of satellite with appendages tracking big angles［J］.Journal of Dynamics and Control，2004，2(2):29-32.

［7］苟兴宇，陈义庆，李铁寿，等.平台与附件同时机动及其复合控制初探［J］.空间控制技术与应用，2009，35(5):1-5.GOU X Y，CHEN Y Q，LI T S，et al.Introduction to simultaneous maneuvers and composite control of spacecraft platform and its appendages［J］.Aerospace Control and Application，2009，35(5):1-5.

［8］XIA Y Q，ZHU Z，FU M Y，et al.Attitude tracking of rigid spacecraft with bounded disturbances［J］.IEEE Transactions on Industrial Electronics，2011，58(2):647-659.

［9］LEVANT A.Robust exact differentiation via sliding mode technique［J］.Automatica，1998，34(3):379-384.

［10］ZHU Z，XIA Y Q，FU M Y.Attitude stabilization of rigid spacecraft with finite-time convergence［J］.International Journal of Robust and Nonlinear Control，2011，21:686-702.

［11］GAWRONSKI W，ALMASSY W T.Command preprocessor for radio telescopes and microwave antennas［J］.IEEE Antenna's and Propagation Magazine，2002，44(2):30-37.