基于摄动能量匹配条件的椭圆参考轨道伴飞构型设计

陈伟跃，黄 震

(北京空间技术研制试验中心，北京100094)

0 引言

交会对接的飞行成功，伴飞和绕飞的工程实现，使得圆参考轨道的相对运动控制技术日趋成熟.椭圆参考轨道的相对运动控制技术，是未来空间相对运动控制的发展趋势，将在诸多科学探测领域发挥重要作用，如欧空局用于探测太阳粒子与地球磁场相互作用的Cluster编队项目［1］，美国航空航天局用于探测地球磁场等离子体机理的编队探测计划［2］.

对于椭圆参考轨道的编队飞行而言，目标星—追踪星构型是最常见的编队飞行构型，采用此构形的伴飞和绕飞研究最为广泛，多数研究都是依据线性化相对运动设计相对轨道［3-6］，再进行位置保持控制消除非线性和摄动对编队的影响［4］.为了维持编队队形，需要进行频繁的位置保持控制.李海阳等［5］以椭圆参考轨道的周期性线性绕飞条件为约束，给出了形式简单直观的椭圆参考轨道周期性相对运动的解析解，并设计了椭圆参考轨道水平圆编队构形.何康乐等［6］通过建立较小偏心率、以真近点角为变量的椭圆一阶无摄动相对运动方程，设计了泪滴形绕飞轨道.上述研究均基于线性化的思路进行，考虑非线性影响的相关研究［7］较少.

如何同时考虑非线性和摄动的影响，直接设计相对轨道并减少位置保持的控制次数是椭圆参考轨道编队领域的重要问题，相关研究较少.本文采用能量匹配的思想对J2摄动下椭圆参考轨道附近的稳定伴飞问题进行了探讨.

1 J2摄动下的能量匹配条件

以目标星轨道作为参考轨道，参考轨道坐标系定义为:坐标原点O在目标星质心，OZt轴指向地心，OYt轴沿目标星的轨道负法线方向，OXt轴与OYt轴和OZt轴构成右手系.当追踪星与目标星的半长轴相等时，轨道能量相等，称为能量匹配条件.考虑J2摄动时，能量匹配条件可以写成如下形式:

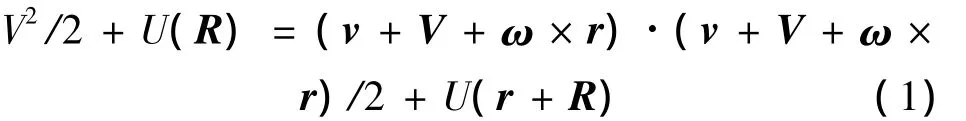
其中U(·)和ω分别为考虑J2摄动的引力势函数和目标星的轨道角速度，R和V分别为目标星的位置矢量和速度矢量，r和v分别为追踪星相对于目标星的相对位置和相对速度.

2 J2摄动下能量匹配条件的利用

将式(1)写成如下形式:

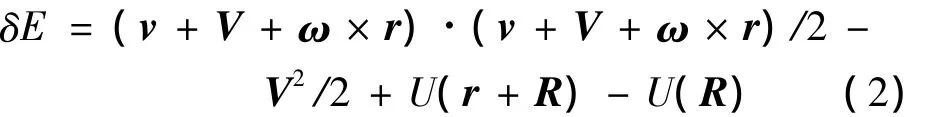
其中ω的分量为

式中，E为轨道能量，δE为轨道能量差，i为参考轨道倾角，u为参考轨道的纬度幅角，R0为初始时刻参考轨道的地心距，h为参考轨道的瞬时角动量，μ为地球引力常数，Re为地球引力模型参考半径.

计算δE对相对速度的梯度，可得

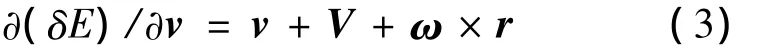
∂(δE)/∂v 为追踪星的绝对速度，其在OXt轴上的分量较另外两个分量大，因此调节OXt方向的相对位置分量更容易使δE=0.当已知相对位置分量xi0，yi0和zi0以及相对速度分量和时，可采用式(4)求相对位置分量

式中，R0为初始时刻参考轨道的地心距，为初始时刻参考轨道的真近点角对时间的导数，上标n表示迭代次数.

若已知初始相对速度vi0，需要确定某一个初始相对位置分量时，采用牛顿迭代法求解.δE对r的梯度为

式中Uc为追踪星的引力势函数，式(5)的第3个分量形式如下:

观察式(5)的分量形式可以发现，∂(δE)/∂r的第3个分量包含ωyRi0i0-η2cR0，其绝对值在3个分量中最大，从而调节zi0更容易使δE=0.当已知相对速度以及xi0和yi0求解相对位置分量zi0时，迭代求解格式为

3 椭圆参考相对运动的描述

其中，

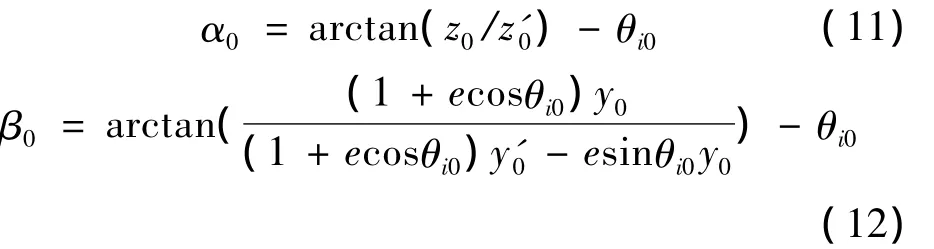
式(8)～(12)中，ρ1表征OXt和OZt方向的相对运动幅度，ρ2表征OXt方向的偏置幅度，ρ3表征OYt方向的相对运动幅度，α0表征参考轨道平面内的相对运动相位，β0表征参考轨道平面外的相对运动相位.ρ1和 ρ3为形状参数，ρ2为偏置参数，α0和 β0为相位参数，ρ1，ρ2，ρ3，α0，β0统称为设计参数.

4 椭圆参考轨道伴飞构型设计

4.1 新伴飞构型

令ρ1与ρ3为0，追踪星与目标星在OXt方向的距离固定为d，ρ2取为 2(1-e2)d/(2+e2)［8］，称为固定距离伴飞.当参考轨道偏心率增大时追踪星与目标星的最小分离距离减小，为了克服此弊端需设计新的伴飞构型.

令伴飞轨迹的中心与目标星的距离为d，相对运动在OXt、OYt和OZt方向的幅度分别为ρx、ρ3和ρ1.以真近点角为独立变量，将式(7)中用有量纲的相对状态表示，进行傅里叶级数展开并［8］保留一阶谐项，得到

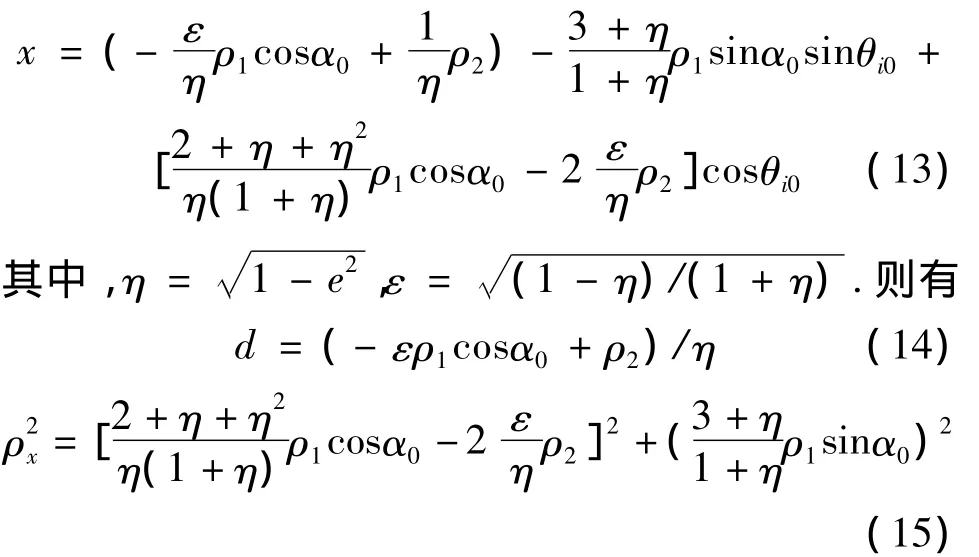
由式(14)可得

将式(16)代入式(15)可得

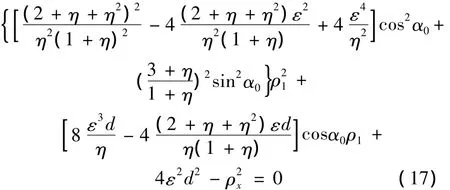
其中，a1、b1、g1、q1、p1由 Bessel函数的0 阶、1 阶和2阶展开式组成，参见参考文献［8］.

通常希望参考轨道平面内和平面外的相对运动相位一致，则有

若OYt方向的幅度不超过OXt方向的幅度，则有［8］

4.2新伴飞构型初始条件的确定

根据新伴飞构型确定设计参数的关键在于求解方程式(17).J2摄动下的能量匹配条件可通过调节或者zi0得以满足，因此在确定设计参数和初始状态时存在两种方法.

第一种方法，J2摄动下的能量匹配条件通过调节得以满足.确定伴飞设计参数的过程如下:首先指定平面内相对运动的相位α0，从而方程(17)为关于ρ1的二次方程，求解该方程得出ρ1.将ρ1代入式(16)可得ρ2.然后根据式(18)和式(19)可得相位β0为

依据α0确定 β0的象限:当 π/2＜α0≤3π/2时，由式(21)得出的β0需要加上π;当3π/2＜α0＜2π时，由式(21)得出的β0需要加上2π.确定β0后，ρ3可根据式(20)确定.至此5个设计参数完全确定.由设计参数确定初始状态的过程如下:由式(8)中的ρ1和式(11)中的α0有

其中，z'i0为zi0对真近点角的导数，将其变换为对时间的导数，可得

将z'i0代入式(9)可得

令yi0与y'i0之比为ky，根据式(12)中β0的表达式可得式(25)，再结合式(10)可得yi0

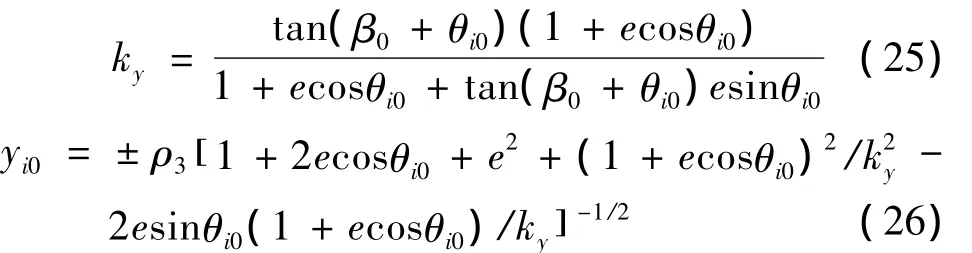
则y'i0和分别为

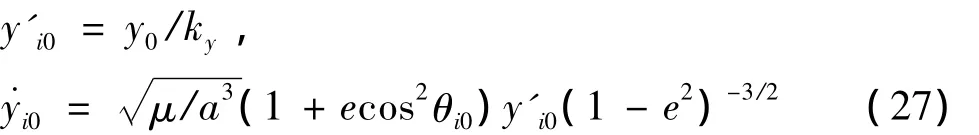
由式(4)迭代确定.至此6个初始相对状态完全确定.

第二种方法，J2摄动下的能量匹配条件通过调节zi0得以满足.给定迭代初值，根据式(8)和式(11)，可得

将式(28)代入式(17)，则式(17)化为 cosα0的四次方程.定义系数A、B、C如下:

方程(17)可重写为如下形式:

式(30)为关于cos2α0的二次方程，当系数A、B和C满足(2AC-B2)2＞4(A2+B2)C2时，可以求出 cos2α0，进而确定 α0.将 α0代入式(28)可确定ρ1，将 ρ1和 α0代入式(16)可确定 ρ2.确定 β0和 ρ3的过程与第一种方法中的对应过程相同.设计参数完全确定之后，可依据设计参数确定初始相对位置和初始相对速度.根据式(22)中zi0的表达式可得

将z'i0代入式(23)可确定，确定xi0、yi0和y'i0的过程与第一种方法中的对应过程相同，最后需要指定.相对状态确定之后，利用式(6)迭代修正zi0，得到新的zi0，重复上述设计参数和初始相对状态的确定过程以及zi0的迭代修正过程，当zi0的取值使J2摄动下的能量匹配条件得到满足时停止迭代，设计参数和初始相对状态随之确定.需要说明的是，A和B表达式中的“∓”号与式(28)右端的“±”号对应，A和B表达式中的“∓”号的选择只需保证方程(30)有合理的解即可.

4.3 伴飞初始化控制策略

在某时刻追踪星相对于目标星的相对位置为r0，相对速度为根据上述新伴飞构型的确定方法，可得出形成伴飞的相对位置ri0和相对速度vi0.因此伴飞初始化问题转化为一个交会问题，以r0和v0为交会的始端条件，以ri0和vi0为交会的终端条件，以T-H方程为基础的交会控制方法可实现椭圆参考轨道的交会［9］，在此不赘述.

5 位置保持修正

5.1 修正脉冲的解析表达式

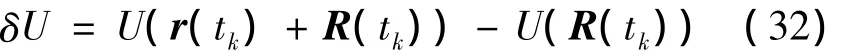
式中，tk为位置保持修正时刻，下标k1表示此状态为tk时刻修正脉冲作用前的状态，则分别为

施加位置保持脉冲后，追踪星相对于目标星的相对状态满足能量匹配条件式(1)，即

为使位置保持修正消耗的燃料尽可能少，需进行优化，约束条件取为式(34)，优化目标函数取为

当tk指定时，上述优化问题可以采用拉格朗日乘子法求解.令拉格朗日乘子为λ，则拉格朗日函数为

当L取极值时，有

由式(34)～(37)可得

将式(38)代入式(34)，可得

当V2＞2δU时可得

当式(34)～(37)描述的优化问题对应的加边Hessian矩阵满足-|Δj|＞0(j=2，3，4)时，H有局部极小值［10］.因此可得 λ＞-2，则有

5.2 修正脉冲的全局优化

以伴飞初始化结束时刻为零时刻，以tk为优化变量，优化目标函数为式(35)，约束条件为0≤tk≤tmax，求解最佳位置保持时刻和位置保持脉冲的问题为动态优化问题，可采用遗传算法、序列二次规划等方法求解.相对状态的传播可采用如下方法:以平根近似传播追踪星和目标星的绝对状态，将两者的绝对状态作差获得相对状态.

6 数学仿真

参考轨道为Molniya轨道，初始时刻的轨道根数为:半长轴为 26 553.375 km，偏心率为 0.741 0，轨道倾角为 63.4°，近地点幅角为 270°，升交点赤经为329.480°，真近点角为180°，轨道摄动考虑J2摄动.

对于新伴飞构型取d=10 km，ρx=1 km.两种构型均用式(20)确定ρ3.伴飞初始化误差取为δr=［0.1 0.01 0.01］Tkm，δv=［0.01 0.01 0.01］Tm/s.tmax为一个轨道周期，当|δE|＜1×10-7时，认为J2摄动下的能量匹配条件得到满足.新伴飞构型的设计参数和形成伴飞的初始状态如表1所示.其中ρ1～3的3行分别对应 ρ1，ρ2，ρ3，ri0、vi0和 Δvk的3 行为 3 个方向对应的分量.图1～4为采用两种方法确定设计参数和伴飞初始状态对应的仿真结果.图中的虚线表示无伴飞初始化误差时的相对轨迹，显示的时间长度为1个参考轨道周期，点线表示有伴飞初始化误差且在位置保持修正之前的相对轨迹，对应的时间长度为tk，实线表示有伴飞初始化误差且经过位置保持修正后的相对轨迹，对应的时间长度为10个参考轨道周期.

仿真结果表明，当满足J2摄动下的能量匹配条件时，即使参考轨道偏心率较大亦能形成稳定的伴飞.两种方法所得的伴飞轨迹在OXt方向的相对运动范围约为8～12 km，设计范围为9～11 km，新伴飞构型及其设计方法能有效减小分离距离的设计偏差.

图1 方法1伴飞三维轨迹Fig.1 3D formation trajectory with methodⅠ

图2 方法1伴飞X-Z投影Fig.2 X-Z projection of formation with methodⅠ

7 结论

数学仿真表明，本文给出的J2摄动能量匹配条件及其利用方法、新的伴飞构型及确定构型参数和伴飞初始相对状态的方法以及位置保持脉冲的解析计算方法均正确有效.利用J2摄动下的能量匹配条件能形成稳定的伴飞，采用新的伴飞构型及其设计方法能明显减小伴飞分离距离的设计偏差.

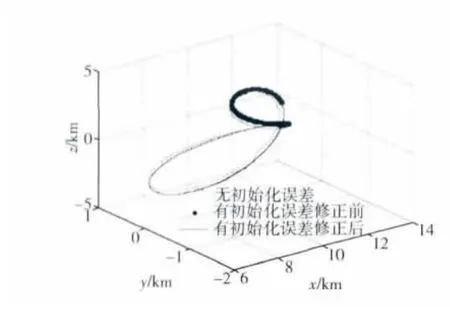
图3 方法2伴飞三维轨迹Fig.3 3D formation trajectory with methodⅡ

图4 方法2伴飞X-Z投影Fig.4 X-Z projection of formation with method Ⅱ

表1 伴飞轨迹的设计参数和形成伴飞的初始状态Tab.1 Design parameters and initial conditions of formation

［1］ESCOUBET C，FEHRINGER M，GOLDSTEIN M.Introduction the cluster mission［J］.Annales Geophysicae，2001，19(1):1197-1200.

［2］CURTIS S.The magnetospheric multiscale mission:resolving fundamental processes in space plasmas［C］//Report Conference of the NASA Science and Technology Definition Team for the Magnetospheric Multiscale Mission，Washington:NASA，1999:1-10.

［3］SENGUPTA P，Vadali S.Relative motion and the geometry of formations in keplerian elliptic orbits［J］.Journal of Guidance，Control and Dynamics，2007，30(4):953-964.

［4］YAMADA K，SHIMA T，YOSHIKAWA S.Effects of perturbation on formation flights around an eccentric reference orbit［J］.Journal of Space Engineering，2008，1(1):69-78.

［5］李海阳，杏建军，唐国金，等.椭圆参考轨道水平圆构形编队设计与演化［J］.宇航学报，2008，29(3):817-820.LI H Y，XING J J，TANG G J，et al.The projection circular orbit design and evolution in elliptical orbits［J］.Journal of Astronautics，2008，29(3):817-820.

［6］何康乐，和兴锁，宋明，等.基于椭圆形参考轨道的航天器泪滴形绕飞轨道设计［J］.西北工业大学学报，2012，30(1):151-156.HE K L，HE X S，SONG M，et al.Designing teardrop-shaped diversion orbit of spacecraft based on elliptic reference orbit［J］.Journal of Northwestern Polytechnical University，2012，30(1):151-156.

［7］杏建军，唐国金，郗晓宁，等.椭圆参考轨道编队卫星非线性周期性相对运动条件［J］.清华大学学报(自然科学版)，2006，46(8):1462-1465.XING J J，TANG G J，XI X N，et al.Nonlinear and periodic relative motion in spacecraft formations in eccentric orbits［J］.Journal of Tsinghua University(Science and Technology)，2006，46(8):1462-1465.

［8］SENGUPTA P，VADALI S R.Relative motion and the geometry of formations in keplerian elliptic orbits［J］.Guidance，Control and Dynamics，2007，30(4):953-964.

［9］荆武兴，陈伟跃.摄动椭圆参考轨道上的最优精确交会［J］，中国空间科学技术，2011，31(2)，16-24.JING W X，CHNE W Y.Fuel-optimal precise rendezvous guidance law in elliptical reference orbit withJ2perturbation［J］.Chinese Space Science and Technology，2011，31(2)，16-24.

［10］MAGNUS J R，NEUDECKER H.Matrix differential calculus with applications in statistics and econometrics［M］.New York:Wiley Press，1999:103-105.