交会对接绕飞段临界安全轨迹研究*

梁静静，解永春，孙 帅

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

0 引言

交会对接技术是在空间探索中利用多航天器操作的一项关键技术，可用于在轨组装大型航天器、实现轨道平台或空间站的补给、进行航天器在轨维修、人员更换等，包括远程导引段、寻的段、接近段(含绕飞段)、最后平移和靠拢段、对接段等［1］.未来空间站(目标器)对接口可能在V-bar、R-bar、H-bar任一方向［2］，此时要进行绕飞机动以捕获对接轴.考虑到绕飞段两航天器的距离只有几百米以及对时间和燃料消耗的要求，研究以保证安全性为前提的绕飞轨迹设计问题具有一定意义.

在已有的相关研究中，能给出绕飞转移的一般解以进行绕飞轨迹设计但未考虑安全性［3］;或者引入安全约束对绕飞轨迹进行优化，得到绕飞时间和燃料消耗的最优数值解［4-5］，但是目前对于在保证安全性的前提下还不能给出两航天器初始距离、转移时间、燃料消耗等之间一般性的关系或结论.因此本文针对绕飞轨迹的设计问题，以-V-bar至+V-bar、R-bar及H-bar之间的绕飞为例展开研究，给出不会进入球形安全区的临界安全条件下绕飞时间、燃料消耗、初始距离三个量之间的关系曲线并拟合出一般性的关系表达式，最后对拟合误差进行分析发现对轨迹的影响很小.

1 绕飞模型

研究两个航天器的相对运动，选择原点o在目标器质心的相对运动坐标系oxyz:oz轴由目标器指向地心方向(+R-bar);ox轴沿轨道运动的正方向(+V-bar);oy轴垂直于轨道面，与ox轴和oz轴成右手坐标系［2］.绕飞段两航天器相对距离较近，对于圆轨道上的交会对接，一般采用Hill方程作为相对运动方程就可以满足任务精度要求.Hill方程是基于二体引力、线性化相对运动和圆参考轨道等三个假设条件推导的，方程［2］如下:

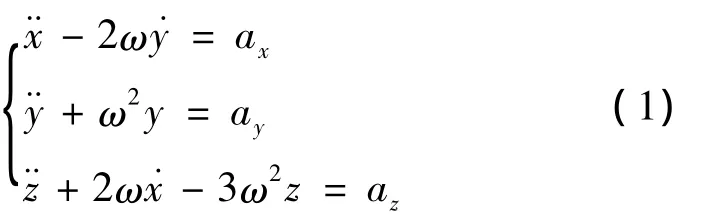
式中，x、y、z分别表示追踪器在相对运动坐标系中的坐标;ω表示目标器轨道角速度;ax、ay、az分别表示三轴机动加速度.令机动加速度为零，上式的一阶解析解(C-W方程)为

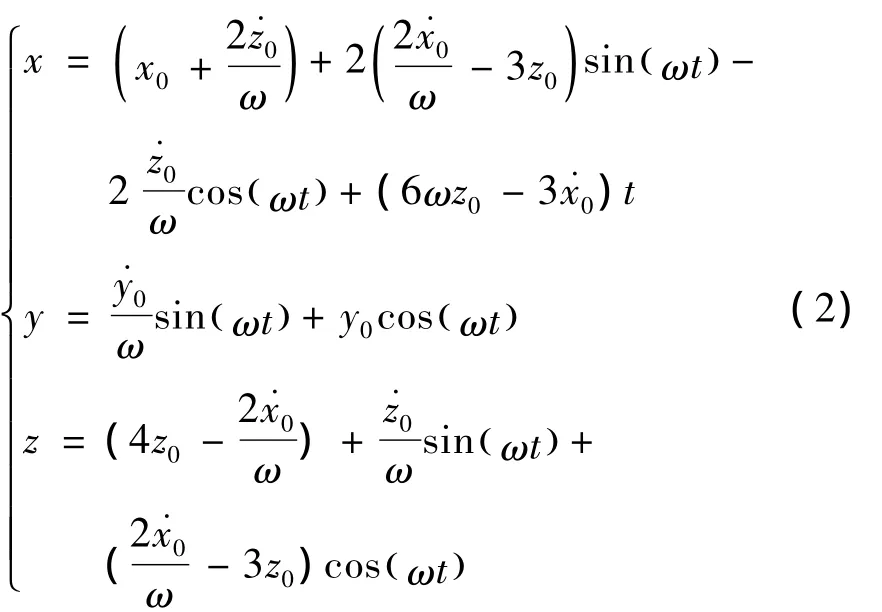
式中，x0、y0、z0及为初始条件.

由C-W方程可知:描述相对运动的轨迹是由初始条件决定的.相对运动可以分解为轨道平面内(xz)的相对运动和垂直于轨道平面(y)的相对运动，两者相对独立，轨道面内的x和z轴的状态相互耦合.

2 问题阐述与分析

设目标器轨道周期为P，绕飞时间为ta，a=ta/P.追踪器绕飞开始前位于-V-bar轴上，与目标器距离为，若目标器的对接口朝向 +V-bar、+R-bar、+H-bar轴时，追踪器要完成相应的绕飞机动.本文采用双脉冲进行绕飞，第一次脉冲在初始位置施加，第二次脉冲在末端位置施加，那么由C-W方程可知:当末端位置确定时，初始位置 (x0，0，0)中的x0、绕飞时间与燃料消耗三个量中已知任意两个量便可确定第三个量，即由其中任意两个量便可确定一条绕飞轨迹.

另外，在绕飞过程中要保证安全，也就是要求整个绕飞期间追踪器的轨迹不进入目标器安全区内.目标器安全区［6］指的是在目标器周围设置的一个综合考虑各种安全约束条件且保证任何情况下追踪器均不能进入的区域.本文假设目标器安全区为球形，半径为Rsafe.设绕飞轨迹上的点到目标器质心的距离为，所以只要满足不等式lmin≥Rsafe即可.

本文的研究按如下思路展开:

(2)将追踪器与目标器的初始距离、绕飞时间设定在一定范围内，在这个范围内通过仿真遍历得到满足lmin≥Rsafe的绕飞轨迹，由此可以绘制x0、绕飞时间与燃料消耗三者的关系曲面;

(3)绘制临界安全条件下的绕飞轨迹所对应的绕飞时间、燃料消耗、x0三个量之间的关系曲线;

(4)通过拟合［7］得到关系曲线的表达式.

下面以-V-bar至+V-bar绕飞为例推导绕飞过程中燃料消耗与x0和绕飞时间ta的关系.

由于-V-bar至+V-bar绕飞仅是轨道面内的运动，所以设轨道平面内初始条件为(x0，0，0，0)，末端状态为 (xf，0，0，0 )，施加的初始脉冲0，，代入式(2)推出绕飞起点需施加的脉冲增量［3］

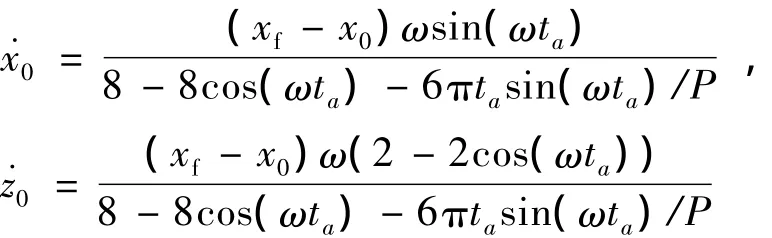
由初始条件和绕飞时间ta可得绕飞终点的速度

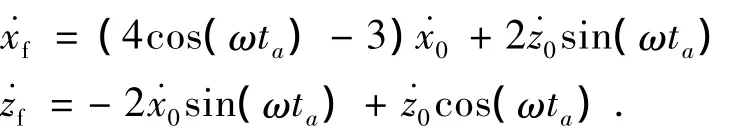
所以要使追踪器相对目标器不动则绕飞终点需施加的脉冲增量为

以下针对 -V-bar到 +V-bar、+R-bar、+H-bar三种绕飞按照上述研究思路进行研究.

3 拟合一般性关系表达式

取目标轨道为400 km的圆轨道，则轨道周期P为5 545 s.设Rsafe=200m ，x0∈ [-600，-200 ].

3.1 从-V-bar到+V-bar绕飞时保证安全的x0、ta和燃料消耗 Δv三者之间的关系表达式

设xf=400 m，图1为保证安全(即lmin＞200)的a、x0和的关系曲面.图2为临界安全条件(即lmin=200)下a、x0和的关系曲线

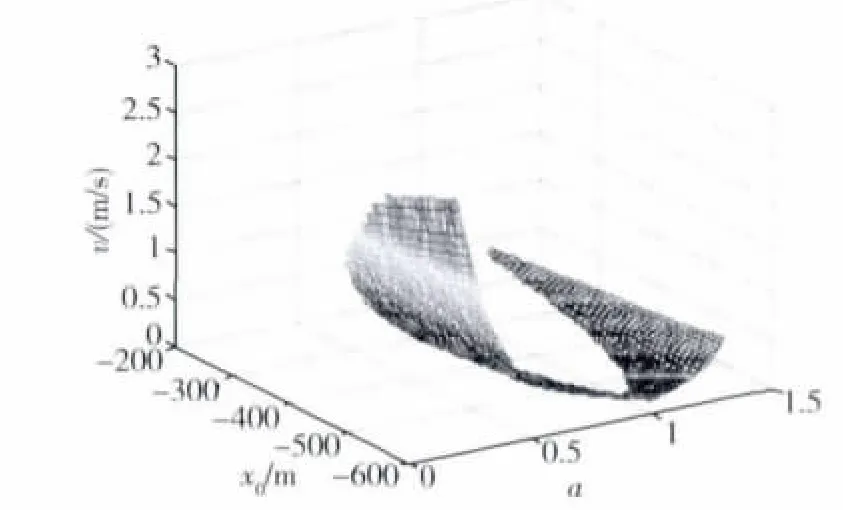
图1 a、x0和 的关系曲面Fig.1 A curved surface about the relation among a、x0and

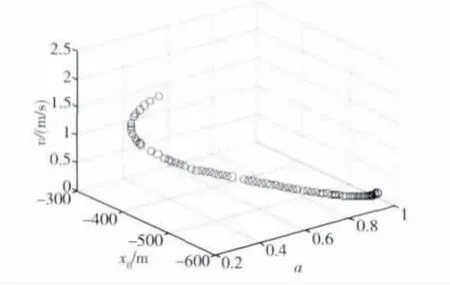
图2 a、x0和 的关系曲线Fig.2 A curve about the relation among a、x0and

1)将图2中的空间曲线投影到底面上并进行拟合，即临界安全条件下a与x0的表达式为

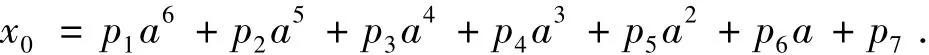
其中系数通过Matlab拟合得到

若采用Δl=lmin-Rsafe的值来衡量安全性，当Δl＞0时，轨迹安全;反之轨迹不安全.由遍历仿真可知:当a给定时，Δl是关于x0的减函数，当x0给定时，Δl随a的增大先增后减.故由上面拟合得到的a与x0的关系表达式:给定a时，可以得到保证安全的最大极限值x0max，即x0≤x0max时轨迹不会进入安全区;反之，给定x0，可以得到保证安全的极限值amin和amax，即amin≤a≤amax时轨迹不会进入安全区.

2)将图2中的空间曲线投影到侧面上并进行拟合，即临界安全条件下，a与的表达式为其中系数为

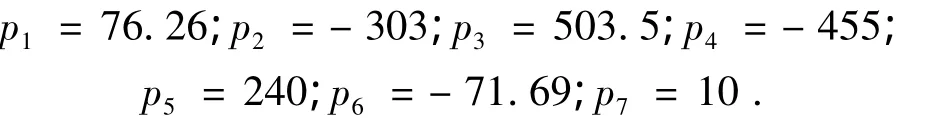
3.2 从-V-bar到+R-bar绕飞时保证安全的x0、ta和燃料消耗三者之间的关系表达式设绕飞终点处:zf=250 m，图3为lmin＞200时，a、x0和的关系曲面.图4为临界安全条件下(lmin=200)时，a、x0和的关系曲线.

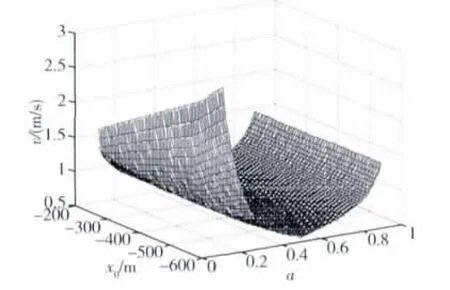
图3 a、x0和的关系曲面Fig.3 A curved surface about the relation among a、x0and

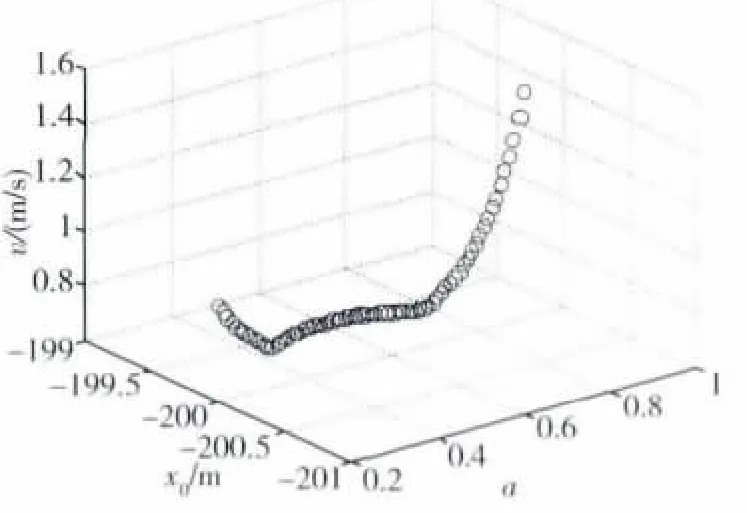
图4 a、x0和 的关系曲线Fig.4 A curve about the relation among a、x0and

1)将图4中的空间曲线投影到侧面上并进行拟合，即临界安全条件下的拟合表达式为

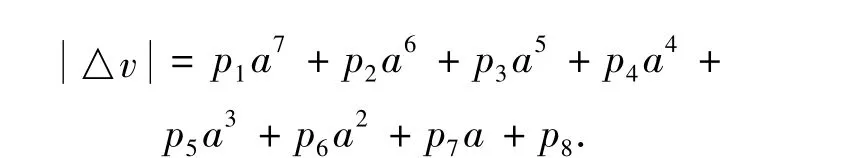
其中系数为

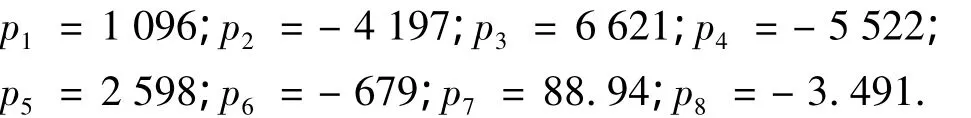
2)将图4中的空间曲线投影到底面上并进行拟合，即临界安全条件下a与x0的拟合表达式

a为任意值时，x0=-200.

3.3 从-V-bar到+H-bar绕飞时保证安全的x0、ta和燃料消耗三者之间的关系表达式

设绕飞终点处:yf=250m，除去不可到达点a=0.5 ，a，x0，lmin的关系曲面如图 5 所示;a，x0，的关系曲面如图6所示.由图5可知，当a∈[0.51，0.9 ]时，a＞0.86时才能保证安全，所以舍掉这一部分，只取a∈[0，0.5]的情况.

当a∈ [0.1，0.48 ]时，临界安全条件下(由于lmin=200时对应的临界点太少，因此扩大范围lmin∈ [199，201])，a，x0和的关系曲线如图7所示.

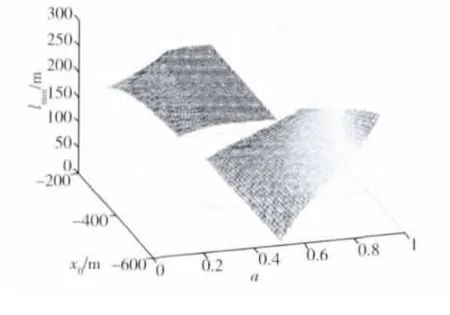
图5 a、x0和lmin的关系曲面Fig.5 A curved surface about the relation among a、x0and lmin

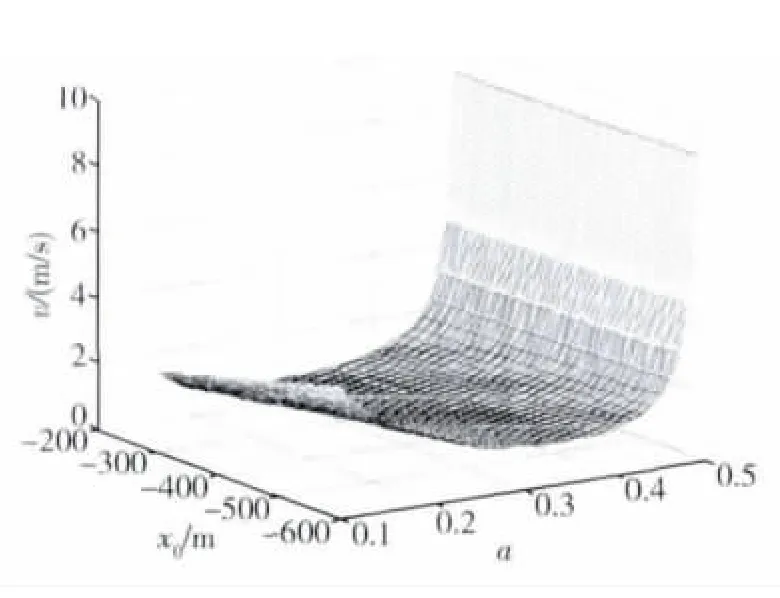
图6 a、x0和的关系曲面Fig.6 A curved surface about the relation among a、x0and

图7 a、x0和的关系曲线Fig.7 A curve about the relation among a 、x0and

1) 将图7中的空间曲线投影到侧面得a和的关系并拟合

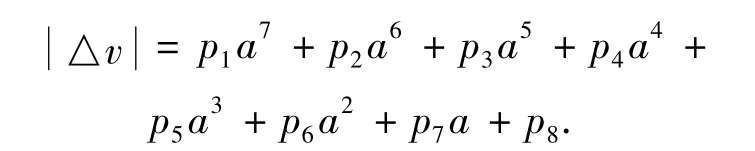
其中系数为

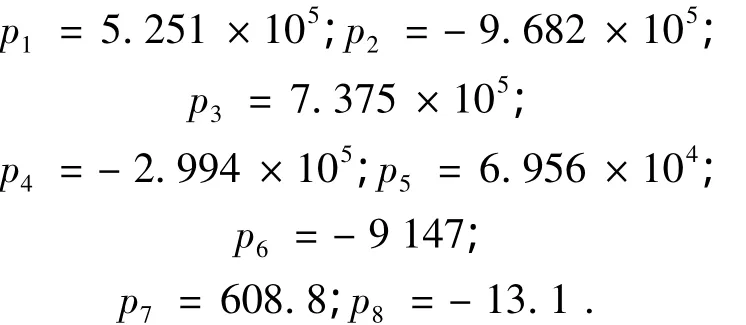
2)将图7中的空间曲线投影到底面得a和x0的关系曲线并拟合

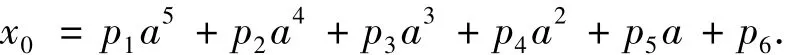
其中系数为

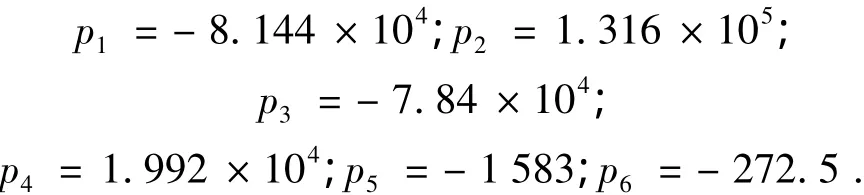
4 对拟合表达式的误差分析

由于拟合表达式存在误差，所以按照拟合表达式计算的参数设计出的绕飞轨迹与临界安全的标称轨迹间存在一定的偏差，可以通过计算轨迹最大偏移量来分析拟合误差对修整使实际轨迹偏离标称轨迹的程度;通过仿真得到轨迹进入安全区的最深距离来分析拟合误差对安全性的影响.

以下为轨迹最大偏移量的计算过程:

(1)假设a的值给定，由临界安全条件下a与x0的拟合表达式得到x0max，进而可以知道施加的径向、切向脉冲的大小，从而确定出绕飞轨迹.

(2)将所有遍历仿真得到的满足临界安全条件的实际绕飞轨迹与对应标称轨迹间的偏差最大值，记为 Δri(i=1，2，…n).

(3)得到轨迹最大偏移量:Δr=max(Δr1，Δr2，…Δrn).

以-V-bar到+V-bar绕飞为例分析拟合误差对实际轨迹偏移标称轨迹的程度以及对安全性的影响.

首先按照上述过程得到整个绕飞过程轨迹最大偏移量Δr=5.456 7 m，即拟合误差导致的实际轨迹偏离标称轨迹的最大距离为5.456 7 m，对绕飞标称轨迹设计的影响较小.

计算轨迹进入安全区的最深距离:假设任意时刻轨迹上任一点到目标器质心的距离记为l(t)，Rsafe-l(t)≤0.337 4m恒成立，即由于轨迹偏差进入安全区的最深点与安全区的边界只有0.337 4m≪Rsafe=200m.由此可知拟合误差导致的轨迹偏差对绕飞的安全性影响很小.

5 结束语

本文采用拟合的方法得到了临界安全条件下从-V-bar至+V-bar、R-bar及H-bar绕飞三种轨迹所对应的绕飞时间、燃料消耗、x0三个量之间的关系表达式，当已知其中任意两个量时便可由拟合表达式求出另一个量，并分析了拟合误差导致轨迹偏离的程度以及对安全性的影响.本文的研究为绕飞段安全轨迹的设计提供了新思路，也为未来空间站(目标器)可能在 V-bar、R-bar、H-bar任一方向对接提供理论基础.

［1］朱仁璋.航天器交会对接技术［M］.北京:国防工业出版社，2007:23-27.

［2］FESHE W.Automated rendezvous and docking of spacecraft［M］.Cambridge，United kingdom:Cambridge University Press，2003:13-16.

［3］朱仁璋，汤溢.空间交会接近与绕飞设计［J］.中国空间科学技术，2005，25(1):7-14.ZHU R Z，TANG Y.Design methods for the closing and fly-around of space rendezvous［J］.Chinese Space Science and Technology，2005，25(1):7-14.

［4］梁静静，解永春.基于粒子群算法优化双脉冲绕飞问题［J］.中国空间科学技术，2013，39(5):43-47.LIANG J J，XIE Y C.Double-impulsive fly-around problem based on particle swarm optimization algorithm［J］.Chinese Space Science and Technology，2013，39(5):43-47.

［5］王华，唐国金.用遗传算法求解双冲量最优交会问题［J］.中国空间科学技术，2003，23(1):26-30.WANG H，TANG G J.Solving optimal rendezvous using two impulses based on genetic algorithms［J］.Chinese Space Science and Technology，2003，23(1):26-30.

［6］林来兴.空间交会对接技术［M］.北京:国防工业出版社，1995:34-35.

［7］龚纯，王正林.精通MATLAB最优化计算［M］.北京:电子工业出版社，2009:51-53.