大型控制力矩陀螺动力学精细建模与仿真*

刘宝玉，金 磊，贾英宏

(北京航空航天大学宇航学院，北京100191)

0 引言

SGCMG具有效率高、输出力矩大、带宽大和线性范围大的特点，是航天器重要的姿态控制执行机构.SGCMG由于其组成与结构特性而存在多种误差与扰动，这此误差与振动影响航天器的姿态控制精度.目前国内外已有很多学者对其进行分析与研究［1-4］，大型SGCMG框架转速一般不采用电机直接控制，而是在框架电机与框架之间加装大减速比的减速机构(如直齿轮、谐波齿轮)以提高框架转速的控制精度，相对于不带减速机构的SGCMG，其结构更为复杂，制造更加困难，误差与干扰的来源也更多，更有必要对其进行精细建模与分析.

大型SGCMG由转子系统和框架伺服系统组成.其中转子系统主要包括:转子组件，转子支承轴承组件，转子驱动电机组件.框架系统主要包括框架组件，框架支承轴承组件，谐波齿轮传动系统组件，框架驱动电机组件.本文将对SGCMG以上各组成部分建立相应模型，以建立大型SGCMG动力学精细模型.

1 转子动力学方程与框架动力学方程

1.1 坐标系定义

为了描述SGCMG中各体之间的相对运动，定义如下坐标系［4］:(1)惯性坐标系fe(oexeyeze);(2)星体坐标系fb(obxbybzb);(3)框架坐标系fg(ogxgygzg)，认为框架质心与形心重合.(4)框架参考坐标系fs(osxsyszs);(5)转子准几何体坐标系ff(ofxfyfzf)，认为转子轴承是刚性支承，转子几何轴与轴承中心线重合;(6)转子几何体坐标系fw(owxwywzw);(7)转子惯量主轴坐标系fI(oIxIyIzI).

1.2 变量定义

记E为三阶单位矩阵，RΓ(Θ)为绕坐标系的Γ轴旋转Θ弧度，定义如下变量:

(1)ρw为点ow至点oI的矢径在坐标系fw中的分量列阵，表征转子的静不平衡;

(2)RIw为坐标系fw到坐标系fI的转换矩阵，表征转子的动不平衡，记为RIw=Ry(μ)Rz(η)，其中μ和η是转子惯量主轴与对应几何轴偏离的角度;

(3)mw为转子质量.

(5)Ω为坐标系fw相对于坐标系ff的角速度在坐标系ff中的分量列阵;

(6)Rwf为坐标系ff到坐标系fw的转换矩阵;

(7)rfg为点og至点of的矢径在坐标系fg中的分量列阵，表征框架质心与转子几何中心的不重合度;

(8)Rfg为坐标系fg到坐标系ff的转换矩阵，表征转子轴的安装方位偏差，记Rfg=Rx(ψ)Ry(β)Rz(α)，其中，α、β和ψ是转子轴安装误差带来的小角度;

(9)mg为框架质量;

(10)Ig为框架在坐标系fg中的惯量矩阵，记Ig=diag{Igx，Igy，Igz};

(11)δ为坐标系fg相对于坐标系fs的旋转角度在坐标系fs中的分量列阵;

(12)Rgs为坐标系fs到坐标系fg的转换矩阵;

(13)rgb为点ob至点og的矢径在坐标系fb中的分量列阵，表征SGCMG在星体上的安装位置;

(14)Rsb为坐标系fb到坐标系fs的转换矩阵，表征SGCMG在星体上的安装方位;

(15)v为点ob的绝对速度在坐标系fb中的分量列阵;

(16)ω为星体的绝对角速度在坐标系fb中的分量列阵.

1.3 转子动力学方程

为了得到转子干扰力矩，在坐标系ff中建立转子的动力学方程.转子的动量pwf和其相对于点of的绝对动量矩表示在坐标系ff中为

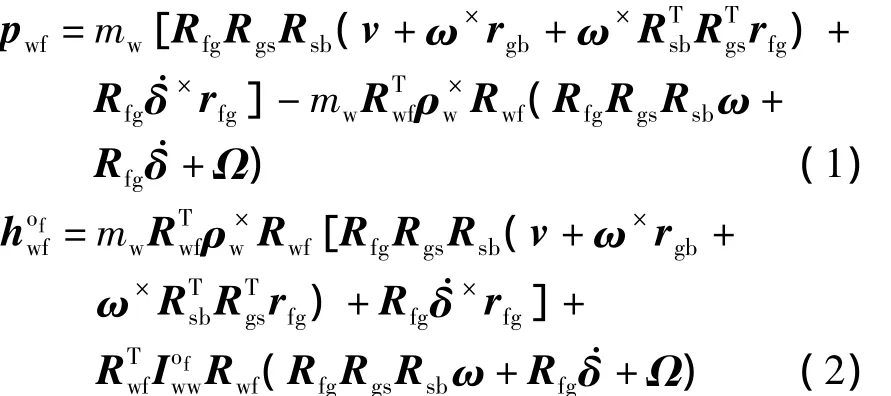
利用动量矩定理可以得到转子在坐标系ff表示的转运动力学方程为

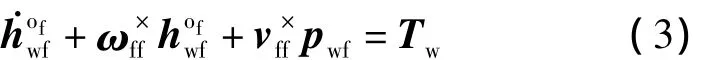
式中，Tw为外部力矩，代表转子电机和转子支承轴承等对转子的作用力矩;ωff为坐标系ff的绝对角速度在坐标系ff中的分量列阵;vff为坐标系ff原点的绝对速度在坐标系ff中的分量列阵

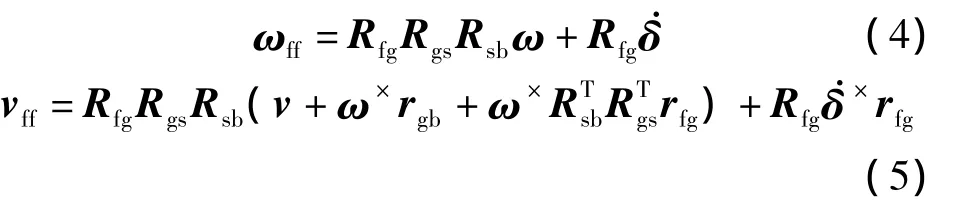
式(3)展开并整理后得到

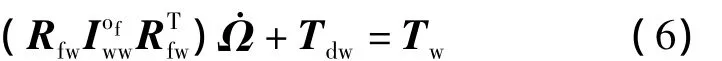
式中Tdw为转子干扰力矩.

1.4 框架动力学方程

为了得到框架干扰力矩，在坐标系fg中建立框架动力学方程［3］.转子的动量pwg和其相对于点og的绝对动量矩示在坐标系fg中为

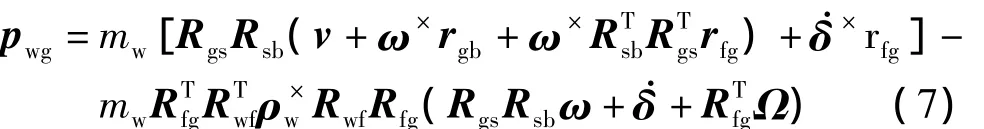
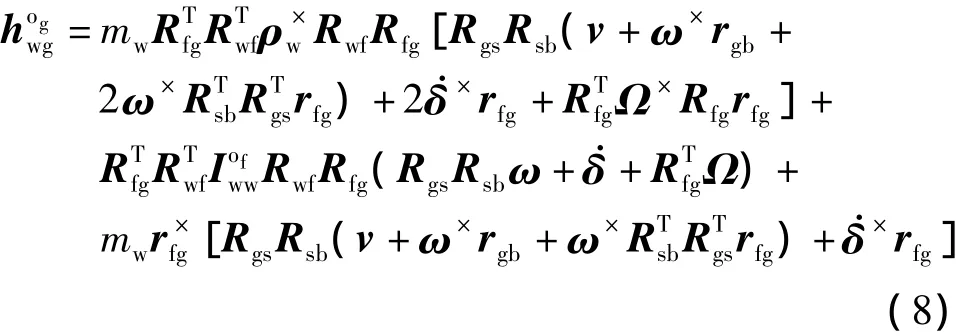
框架的动量pgg和其相对于点og的绝对动量矩在坐标系f中为g

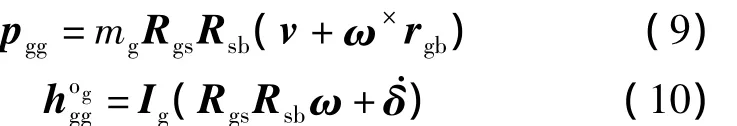
这样，整个转子和框架的动量及其相对于点og的绝对动量矩表示在坐标系fg中为

利用动量矩定理可以得到在坐标系fg下表示的框架转动动力学方程为

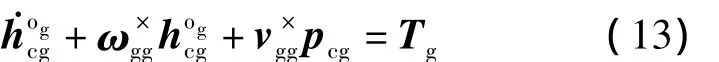
式中，Tg为外部力矩，代表谐波齿轮柔轮和框架支承轴承等对框架的作用力矩;ωgg为坐标系fg的绝对角速度在坐标系fg中的分量列阵;vgg为坐标系fg原点的绝对速度在坐标系fg中的分量列阵.

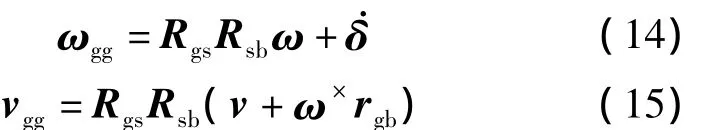
式(13)展开并整理后得到

式中Tdg为框架干扰力矩.

2 摩擦力矩

2.1 转子摩擦力矩

考虑到转子运转在高速状态，转子轴所受摩擦力矩采用静摩擦模型、库仑模型、黏滞模型和Stribeck模型的组合模型［5］表示为

式中，Tfw为转子轴所受摩擦力矩;Tt为转子轴驱动力矩;为角速度，在这里代表转子角速度;Tcou=Kcsgn()，Kc为库仑摩擦力矩;Tvis=Kv，Kv为黏性摩擦系数;Tm为最大静摩擦力矩;s为Stribeck速度;ε为Stribeck模型参数;函数sgn(x)为符号函数.

2.2 框架摩擦力矩

由于框架转速低，本文框架轴所受摩擦力矩采用库仑模型、黏性模型和Dahl模型的组合模型表示，该组合模型可以基本完整地描述摩擦力矩的动态特性和静态特性，且模型简单，因此广泛应用于航空航天领域.框架轴所受摩擦力矩表示为

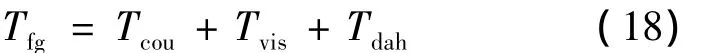
式中，Tfg为框架轴所受摩擦力矩;Tcou与Tvis的含义和表达式与式(17)相同;Tdah为Dahl模型摩擦力矩，Tdah(θ)对时间的导数表示为［6］

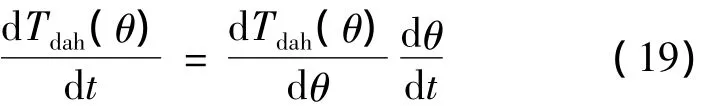
式中

式中，θ表示旋转角度，在这里代表框架转角;σ为静态刚度;λ为与描述的材料有关的常数.

3 谐波齿轮传动系统

谐波齿轮传动系统可以看成是两输入两输出系统，如图1 所示［7］.

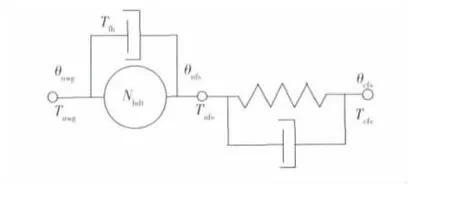
图1 谐波齿轮传动系统特性图Fig.1 Characteristic model of harmonic gear drive system

图中，θnwg为波发生器输入转角(由于波发生器与框架电机轴刚性连接，故这里为框架电机轴转角);Tnwg为波发生器输入力矩;Tfh为谐波齿轮啮合摩擦力矩;Nhdt为谐波齿轮传动比;θnfs为柔轮前端转角;Tnfs为柔轮前端所受力矩，其数学表达为Tnfs=为柔轮刚度系数，Kst为柔轮阻尼系数，α为拟合系数，Δθ为柔轮变形转角，Δθ= θnwg/Nhdt- θcfs;θcfs为柔轮后端转角;Tcfs为柔轮输出力矩，Tcfc=Tnfs;力矩平衡关系为Tnwg=Tnfs/Nhdt+Tfh).

很多学者对谐波齿轮啮合摩擦力矩进行研究，文献［8］中用静态+黏滞+库仑摩擦力矩来表示谐波齿轮传动摩擦力矩，Gandhi等［9］用LuGre摩擦模型和一个基于角位置摩擦模型的组合模型来表示谐波齿轮传动摩擦力矩，Tuttle等［10］建立基于角速度和角位置的谐波齿轮非线性摩擦模型，Taghirad等［7］以库伦模型+黏性模型和Stribeck模型的组合模型来描述，由于这种组合模型的参数便于拟合，本文采用库仑模型、黏滞模型和Stribeck模型的组合模型表示谐波齿轮啮合摩擦力矩，如下所示:

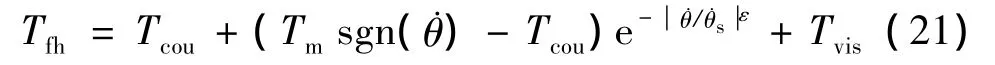
式中、Tcou、Tm、ε 与Tvis的表达式和含义与式(17)相同，在这里代表.

4 数学仿真分析

结合以上对大型SGCMG各主要组成部分的特性、误差及扰动的分析，建立起大型SGCMG的动力学精细模型并进行数学仿真，得到其输出力矩及频谱;转子驱动电机采用无刷直流电机(BLDCM，brushless direct current motor)，其转速控制采用文献［11］的锁相环转速控制方法;框架驱动电机采用正弦永弦同步电机(PMSM，Permanent maynet synchronous motor)，其转速控制采用id为0策略的矢量控制方法.仿真中不考虑SGCMG基座即航天器本体的运动，取转子期望转速和转子电机初始转速均为6 000 r/min;框架期望角速度和框架电机初始转速均为5(°)/s，SGCMG输出力矩表示在坐标系fg中，仿真中所涉及到的主要参数取值如表1～表3所示.

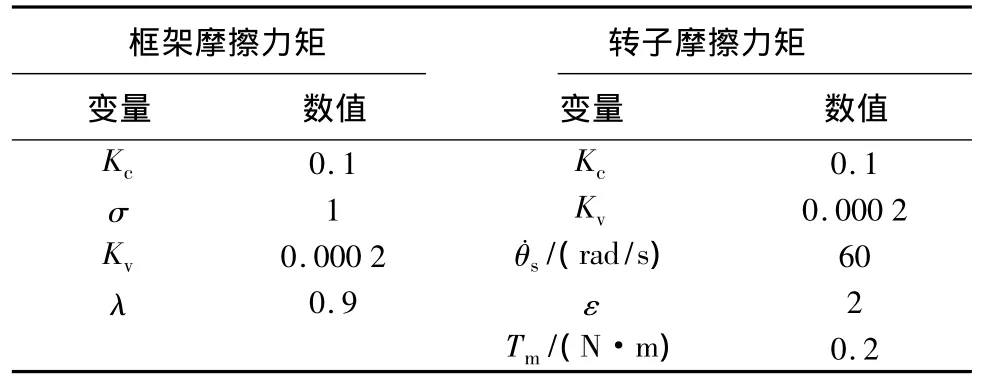
表1 摩擦力矩参数Tab.1 Parameters of bearing friction models

不考虑任何误差与干扰的SGCMG理想模型输出力矩图如图2所示，只考虑框架电机特性(未加装谐波齿轮)时SGCMG的输出力矩图如图3所示，只考虑框架电机特性和谐波齿轮特性时SGCMG的输出力矩图如图4所示，只考虑框架电机、谐波齿轮和转子电机特性时SGCMG的输出力矩图如图5所示，只考虑框架电机、谐波齿轮和转子电机特性和转子动不平衡时SGCMG的输出力矩如图6所示，SGCMG精细模型的输出力矩及其频谱图如图7和图8所示.

表2SGCMG参数Tab.2 Parameters of SGCMG

表3 谐波齿轮传动系统参数Table.3 Parameters of harmonic gear drive system

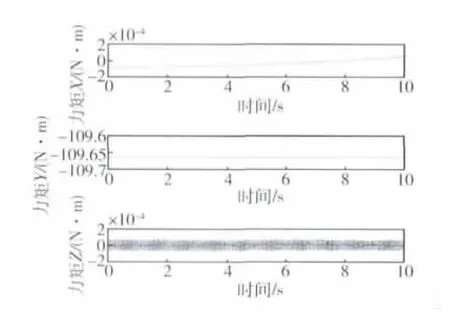
图2 SGCMG理想模型输出力矩Fig.2 Output torque of SGCMG ideal model

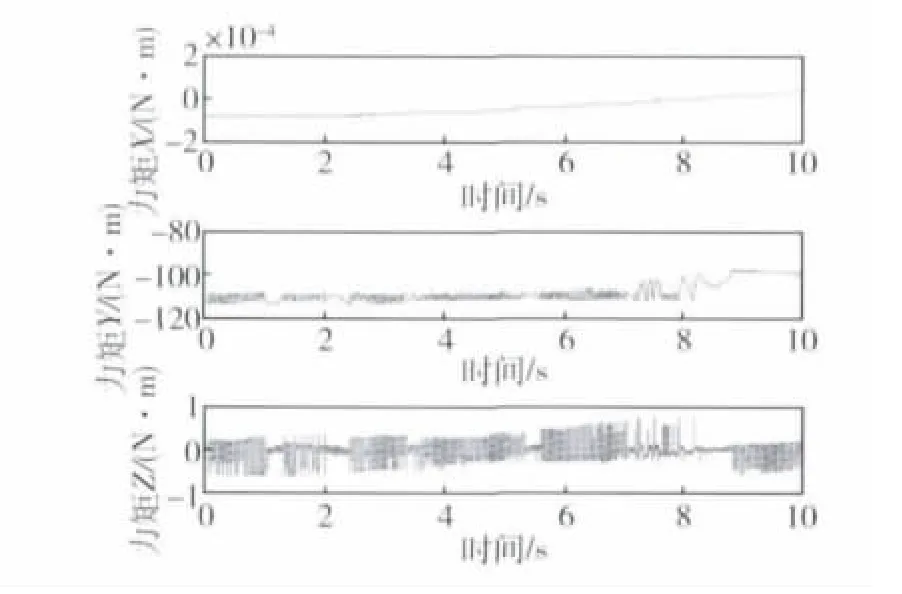
图3 只考虑框架电机特性时SGCMG输出力矩Fig.3 Output torque of SGCMG considering the characteristics of gimbal motor

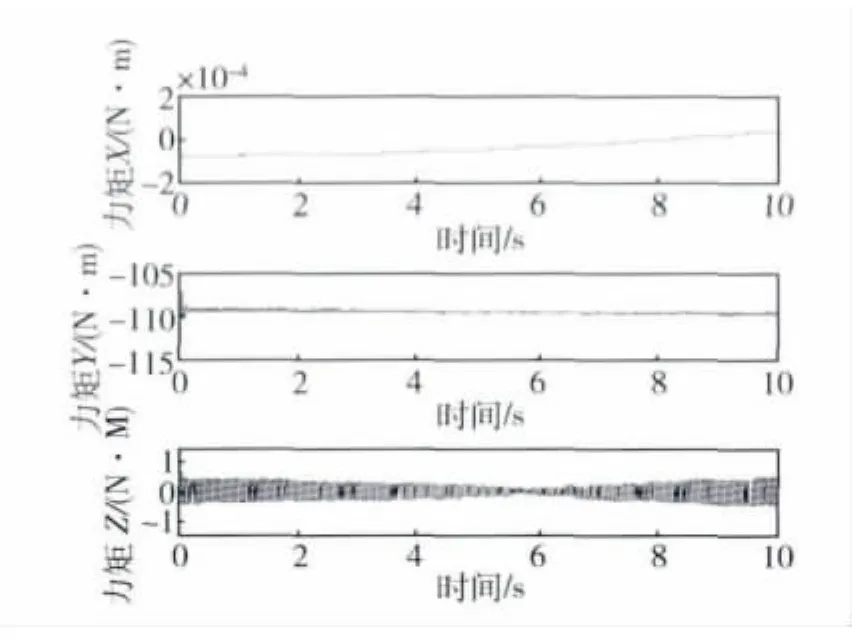
图4 只考虑框架电机和谐波齿轮特性时SGCMG输出力矩Fig.4 Output torque of SGCMG considering the characteristics of gimbal motor and harmonic gear

图5 只考虑框架电机、谐波齿轮和BLDCM特性时SGCMG输出力矩Fig.5 Output torque of SGCMG considering the characteristics of gimbal motor，harmonic gear and BLDCM

图6 只考虑框架电机、谐波齿轮和BLDCM和转子动不平衡时SGCMG输出力矩Fig.6 Output torque of SGCMG considering the characteristics of gimbal motor，harmonic gear，BLDCM and rotor dynamic imbalance

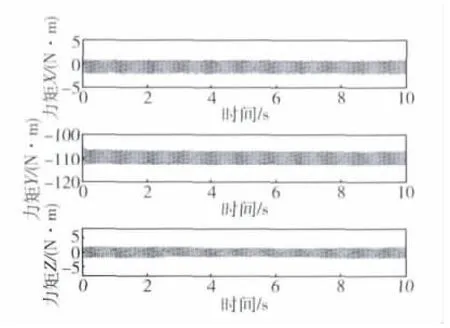
图7 SGCMG精细模型输出力矩Fig.7 Output torque of SGCMG fine model

图8 SGCMG精细模型输出力矩频谱Fig.8 Output torque frequency spectrum of SGCMG fine model

由以上数学仿真结果可知:框架伺服系统不加装谐波齿轮减速机构时，SGCMG输出力矩偏差较大;在框架伺服系统加装谐波齿轮减速器可以明显提高输出力矩精度，同时也给框架轴带来高频谐振.转子电机在xg轴方向产生高频振荡的扰动力矩.转子动不平衡在yg轴和zg轴方向造成周期扰动力矩;使框架角加速度周期振荡，是导致SGCMG在yg轴和zg轴方向产生输出力矩偏差的主要原因;相比之下，转子静不平衡和转子轴安装误差对SGCMG输出力矩的影响相对较小.

由图8可知SGCMG输出力矩的频谱特性表现为:SGCMG输出力矩的xg轴分量因受转子电机的影响主要分布在高频处.yg轴分量主要分布在低频(框架转速频率)处;其次是在转子转速频率(100 Hz)处，为由转子动不平衡造成的扰动力矩;zg分量主要分布在转子转速频率(100 Hz)处，为转子动不平衡造成的扰动力矩;其次是在高频(1 600 Hz附近)处，主要受谐波齿轮的影响.

5 结论

本文分析了SGCMG各主要组成部分、误差及扰动的特性与模型，通过建立大型SGCMG动力学精细模型和理想模型并进行数学仿真，结果表明:在框架伺服系统加装谐波齿轮减速机构可以明显提高SGCMG输出力矩精度，同时也给框架带来高频谐振;转子电机会使SGCMG在其转子轴方向产生高频振荡的扰动力矩;转子动不平衡在SGCMG力矩输出轴和框架轴方向造成与转子转速频率同频的扰动力矩，是导致SGCMG在其力矩输出轴和框架轴方向产生输出力矩偏差的主要原因;相比之下，转子静不平衡和转子轴安装误差对SGCMG输出力矩的影响相对较小.

［1］杨秀彬，常琳，金光.单框架控制力矩陀螺转子动不平衡对遥感卫星成像的影响［J］.中国光学，2012，5(4):358-365.YANG X B，CHANG L，JIN G.Influence of dynamic imbalance of SGCMG rotor on remote sensing satellite imaging［J］.Chinese Optics，2012，5(4):358-365.

［2］吴忠，吴宏鑫.SGCMG框架伺服系统扰动力矩的分析与抑制［J］.航天控制，1998(4):9-18.WU Z，WU H X.Analysis and attenuation of disturbance torque in SGCMG gimbal servo systems［J］.Aerospace Control，1998(4):9-18.

［3］张尧，金磊，徐世杰.小型控制力矩陀螺扰动建模及性能指标分析［J］.中国空间科学与技术，2012(4):45-53.ZHANG Y，JIN L，XU S J.Disturbance modeling and performance index evaluation of the small control moment gyroscope［J］.Chinese Space Science and Technology，2012(4):45-53.

［4］金磊，徐世杰.SGCMG框架伺服系统动力学建模与低速控制［J］.中国空间科学与技术，2010，30(5):1-10.JIN L，XU S J.Dynamics modeling and low rate control of gimbal servo system for single gimbal control moment gyro［J］.Chinese Space Science and Technology，2010，30(5):1-10.

［5］刘丽兰，刘宏昭，吴子英，等.机械系统中摩擦模型的研究进展［J］.力学进展，2008，38(2):201-213.LIU L L，LIU H Z，WU Z Y，WANG Z M.An overview of friction models in mechanical systems［J］.Advances in Mechanics，2008，38(2):201-213.

［6］CANUDAS DE W C，OLSSON H，LISCHINSKY P.A new model for control of systems with friction［J］.IEEE Transactions on Automatic Control，1995，40(3):419-425.

［7］TAGHIRAD H D，BELANGER P R.An experimental study on modeling and identification of harmonic drive systems［C］//Decision and Control，Japan:IEEE，1996:4725-4730.

［8］李刚俊.一种用于精确位置控制的谐波齿轮数学模型分析［J］.机械传动，2010，34(1):26-29.LI G J.Analysis of a mathematical model for precise harmonic gears transmission system［J］.Journal of Mechanical Transmission，2010，34(1):26-29.

［9］GANDHI P S.Modeling and control of nonlinear transmission attributes in harmonic drive systems［D］.Houston:Rice University，2001.

［10］TUTTLE T D ，WARREN P S.A nonlinear model of a harmonic drive gear transmission［J］.IEEE Transactions on Robotics and Automation，1996，12(3):368-374.

［11］王京锋，孙纯祥.软件锁相环技术在陀螺用无刷直流电机高精度稳速控制中的应用研究［J］.微电机，2006，39(2):46-50.WANG J F，SUN C X.Application research of SPLL technology in high precision speed control of BLDCM used in gyro［J］.Micromotors，2006，39(2):46-50.