基于ANSYS工字钢截面力学优化设计

徐 莹

(河北省大厂职业教育中心，河北廊坊 065300)

0 引言

工字钢是工程上普遍使用的一种钢材，由于工字钢具有横纵两个对称轴，故有优良的力学性能。工字钢成品型号有限，实际工程中经常要在现场采用三块钢板焊接而成满足需要的、不同规格的工字钢。由于长期缺乏理论指导，现场焊接工字钢往往凭经验主义行事，并不能从力学角度上合理确定工字钢的翼缘和腹板的合理尺寸搭配［1－3］。本文，以大型有限元程序 ANSYS 为依托，从力学角度上分别对不同工况条件下工字钢的组合进行受力分析，力求找到工字钢受力特征，并给出合理化建议。

1 有限元模型建立及基本条件

1.1 模型参数条件

工字钢示意图及X、Y坐标(Z坐标垂直纸面向外——工字钢跨度方向)如图1所示，本文分析采用等翼缘工字钢，因为这种工字钢抗拉和抗压受力均衡，有一定代表性［4－5］。三种工况条件如表1所示。

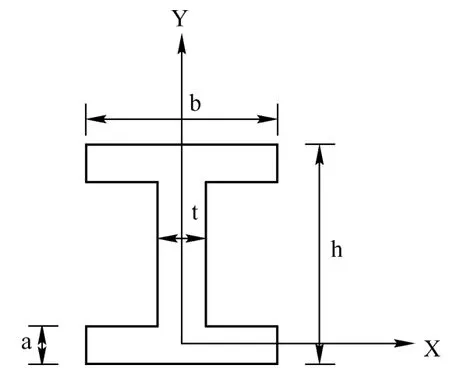
图1 工字钢示意图

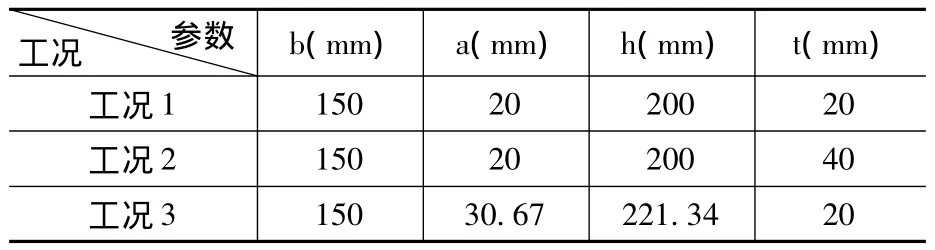
表1不同工况下工字钢参数

1.2 工字钢抗弯性能的理论基础

工字钢抗弯性能除了和工字钢本身材料有关外还和工字钢截面惯性矩密切相关［6－7］。由于工字钢是由三块矩形钢板组成，故对形心轴Y轴惯性矩为:

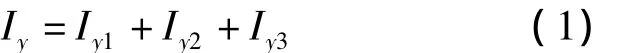
Iy1、Iy3—翼缘处矩形截面对 Y轴惯性矩;Iy2—腹板对Y轴惯性矩。

参照图1，由于矩形截面的惯性矩:

把公式(2)代入公式(1)中，参考图1各个部位尺寸得:

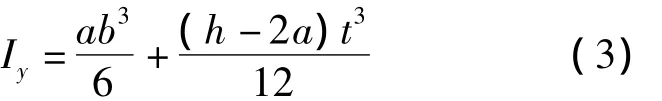
对X轴惯性矩计算过程如下:

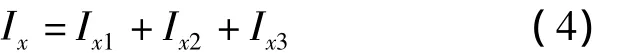
Ix1、Ix3—翼缘处矩形截面对 X轴惯性矩;Ix2—腹板对X轴惯性矩。

由于X轴不是形心轴，考虑到惯性矩平行轴移轴公式［8－9］，得:

把公式(5)、(6)、(7)代入公式(4)中得到截面关于X轴惯性矩Ix为:

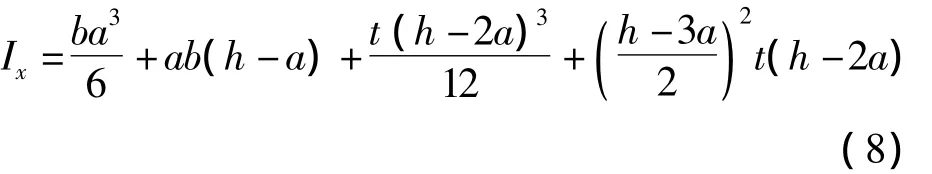
1.3 有限元模型

本文在表1的参数条件基础上，利用大型有限元程序ANSYS进行建模，模型采用SOLID45单元进行模拟，钢材的弹性模量E=190 GPa，泊松比μ=0.3，不计重力。为了更好说明问题，三种工况下上翼缘顶面所受均布压力都为50 MPa。边界条件:模型左右两侧为全固端约束。根据以上条件建立的有限元模型如图2所示。

图2 有限元模型

2 不同工况条件下有限元分析

2.1 工况1

有关工况1条件下，工字钢参数见表1。得到的分析结果如图3～图5所示。

从图3～图5可见，梁的跨中最大挠度值为172.77 mm;X方向最大位移为1.068 mm;YZ方向最大剪力存在于梁的两端，其数值为0.313E10MPa。

图3 工况一条件下Y方向位移

图4 工况一条件下X方向位移

2.2 工况2

工况2和工况1相比只是腹板的厚度从20 mm增加到40 mm，为了研究腹板厚度的增加对工字钢抗弯性能影响程度，得到的数值模拟有关图形如图6～图8所示。

从图6可见，该工字钢Y方向(竖直方向)的最大位移在跨中，即最大挠度值为149.721 mm;从图7可见X方向最大位移为0.974 mm;图8中清楚表现出 YZ方向的最大应力为0.175E10MPa。

图6 工况二条件下Y方向位移

图7 工况二条件下X方向位移

图8 工况二条件下YZ方向剪力

2.3 工况3

工况3和工况1相比增加了上下翼缘的厚度，翼缘从原来的20 mm增加到30.67 mm，翼缘增加的面积等于工况2中腹板加厚而增加的面积，也就是说后两种工况增加的钢材量是相等的。由于翼缘的厚度的增加造成了梁高从原来200 mm增加到221.34 mm。得到的数值模拟有关图形如图9～图11所示。

图9 工况三条件下Y方向位移

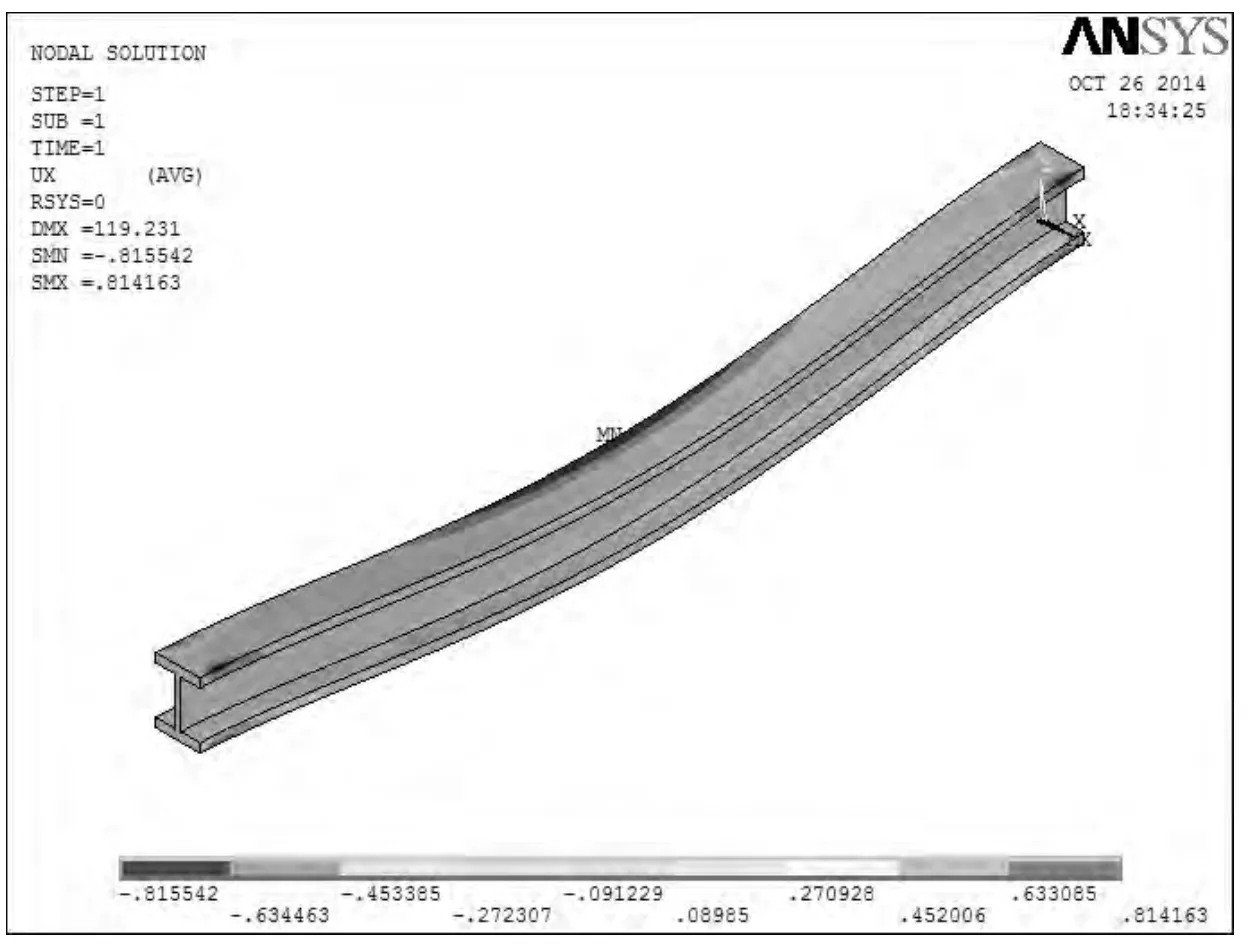
图10 工况三条件下X方向位移

从图9～图11可见，梁的跨中最大挠度值为119.23 mm;X方向最大位移为0.816 mm;YZ方向最大剪力存在于梁的两端，其数值为0.297E10MPa。

3 结果分析

为了便于比较上述三种工况下的数值计算结果，把相应数据汇总到表2中。

通过表2可见:工况2在工况1的基础上腹板增加了20 mm，X方向位移变化很小，而Y方向位移从172.77 mm减少到149.72 mm，减少了13.34%;YZ方向最大应力从0.313E10减少到0.175E10，减少了44.09%。工况3和工况1相比较而言，X方向位移仍然没有发生大的变化，Y方向位移从172.77 mm减少到119.23 mm，减少了30.93%;YZ方向最大应力从0.313E10减少到0.297E10，减少了5.11%。

图11 工况三YZ方向剪力

表2不同工况下计算结果

通过上述分析得到:尽管工况2、工况3对比于工况1而言增加的钢材量是相等的，而表现出效果却不一样，分析表明增加腹板厚度对减少YZ方向最大应力效果明显，YZ方向最大应力直接决定着梁的抗剪切破坏;而增加翼缘的厚度对减少跨中挠度贡献明显。

4 结论

工程实际中对工字梁的要求可能不尽相同，通过本文研究发现，如果梁的剪切破坏是主要控制点的话，那就可以增加梁的腹板的厚度，这样效果会更加明显;而如果跨中挠度是控制点的话，翼缘厚度的增加，往往会得到事半功倍的成效。

［1］ 罗小丰，李国强，孙飞飞等.焊接楔形波纹腹板工字钢梁整体稳定性能研究［J］. 土木工程学报，2013，46(2):88－94.

［2］ 周佳.双轴对称楔形工字钢梁的弹性弯扭屈曲［D］.杭州:浙江大学，2007.

［3］ 童根树.钢结构的平面外稳定［M］.北京:中国建筑工业出版社，2007:122－141.

［4］ Xia Jianguo.Inelastic lateral buckling behavior of steel beams［M］//Computational Methods in Engineering Advance＆Application.Singapore:World Scientific Publishing，1992:139 －144.

［5］ 钱健清.对H型钢特点的进一步分析［J］.钢结构，2001，16(51):16－18.

［6］ 马政.焊接工字钢截面的直接计算［J］.锅炉技术，2000，31(12):4－8.

［7］ E Doege，R Menz，et al.Analysis of Leveling Process Based Upon an Analytic Forming Model［J］.Annals of the CIKP，2002，51(1).

［8］ 中华人民共和国国家标准.钢结构设计规范GB50017－2003［S］. 北京:中国计划出版社，2003.

［9］ 陈骥.钢结构稳定理论与设计［M］.北京:科学出版社，2010.