关于山西煤矿百万吨死亡率GM(1，1)模型预测研究

2014-05-07连会青

华北科技学院学报 2014年11期

连会青，冉伟

(1.华北科技学院，北京东燕郊 101601;2中国矿业大学(北京)，北京 100083)

我国煤炭行业的安全事故仅次于交通事故，位居全国第二。由于煤矿事故多，死亡人数多，造成了我国煤矿百万吨死亡率一直高居不下［1］。山西省既是我国的产煤大省，又是世界五大煤炭主要产地之一，煤炭产量约占全国的三分之一。由于煤层赋存条件非常复杂，地质构造对煤层的破坏十分严重，大部分煤层的开采普遍存在着生产效率低、安全状况差等问题。煤矿的安全生产又是一个庞大而又复杂的系统，受地方经济条件、自然条件、国家政策和采矿技术等因素的影响，这些因素导致煤矿事故高发，安全生产形势十分严峻［2］。因此，对山西煤矿的伤亡事故进行科学的分析预测是很有必要的。本文利用GM(1，1)的动态预测灰色模型，对近几年山西煤矿百万吨死亡率进行了建模与预测。

1 灰色系统预测模型GM(1，1)的建立

1.1 灰色系统预测模型的基本原理

GM(1，1)模拟是目前应用最广泛的灰色系统预测模型。GM(1，1)的含义是:G(grey)灰色，M(model)模型，(1，1)分别表示1阶方程、1个变量。

灰色系统预测把已有的原始数据序列比作随时间变化的不确定量或不确定过程，而后通过一系列数据生成方法，如直接累加法，移动平均法、加权累加法、自适应性累加法等逐步使根本没有规律的、杂乱无章的一组原始数据白化，从而构造相应于微分方程解的模型并做出预报，一般仅要求较少的原始数据就可以构造模型。GM(1，1)模型是在灰色系统预测理论中经常用到的单变量数列预测模型［3，4］，这个模型应用原始非负数据数列，经过累加运算生成另一个数据序列，通过生成数列的矩阵变换，使用最小二乘法，构造白化微分方程，解此方程得到模型计算值，再与原始数据进行比较，得到残差。如果所求的残差或者相对误差比较大，可以采用“残差辨识”方法对模型做修正，从而使得所构造的模型符合较高的精度要求。

1.2 GM(1，1)模型的建立［5，6，7］

GM(1，1)模型是一阶的变量微分方程模型，是目前最广泛应用的灰色系统预测模型。

设X(0)为原始离散非负序列，X(0)={X(0)(j)}(j=1，2，…，n)n 为序列长度。

X(1)={X(1)(j)}(j=1，2，…，n)，其中，m=1，2，…，n，)，X(1)(j)可以建立一阶灰色微分方程模型，即白化形式方程

z(1)为X(1)的相邻的数的算术平均数的相反值生成序列。z(1)={z(1)(j)}(j=1，2，…，n)，其中…，n－1。

1.3 GM(1，1)模型的检验［2］

建立的灰色预测模型GM(1，1)需要进行检验其是否满足精度要求，检验方法通常有三种:残差大小检验，是逐点检验;关联度检验，是模型曲线形状与参考曲线形状接近程度的检验;后验差检验，是对残差分析的统计特征进行检验。

本文采用后验差检验，其公式、步骤如下:

首先求原始离散非负序列x(0)(1)和残差e(0)(k)的平均值:，其中)，其中

其次求原始离散非负序列x(0)(1)和残差e(0)(k)的方差:

利用后验差检验法，可以把精度划分为四级(见表1)。

表1 精度等级

总的来说，好的预测结果要求c越小越好，一般要求c小于0.35，最大不超过0.65;要求p越大越好，一般要求 p大于 0.95，最小不小于 0.70［8，9，10］。

2 对山西煤矿百万吨死亡率的预测［4，5］

2.1 实例应用

选取山西2007－2012年的煤矿百万吨死亡率做GM(1，1)灰色预测，由上述公式建立 GM(1，1)灰色模型:(1)(k+1)=(0.726 －1.9925)e－0.4216k+1.9925，其实际数据与预测数据见表2。

表2 2007－2012年山西省煤矿百万吨死亡率和预测结果

2.2 精度检验［13，14］

原始离散非负序列的平均值:

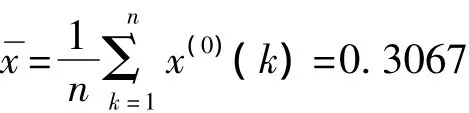
残差得平均值:

原始离散非负序列的方差:

残差的方差:

由以上结果可得出:

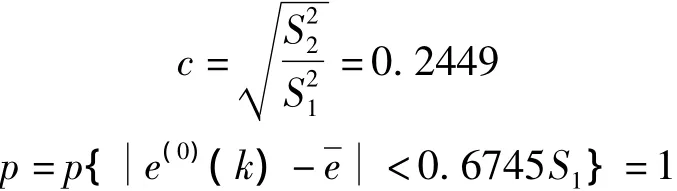
由得出的数据表1进行比较得出结论:预测精度为一级，说明了这种预测模型的准确性和合理性。

2.3 预测结果

由该模型进行预测，令k=6，7，8得出未来三年山西省煤矿的百万吨死亡率。预测结果见表3。

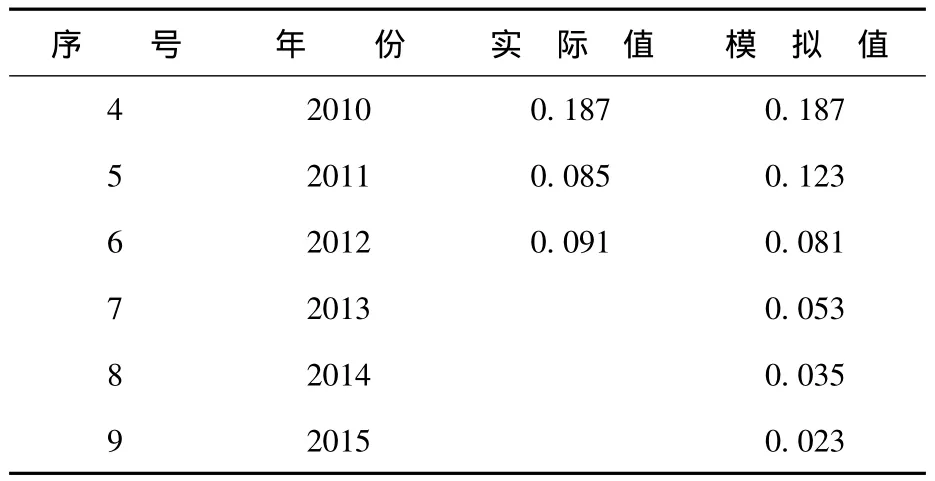
表3 煤矿百万吨死亡率预测结果

2.4 结果分析

由该模型得出的预测结果可以知道，山西煤矿百万吨死亡率呈现不断递减的态势，虽然2012年的实际值比2011年的实际值大0.006，但是近几年的总趋势还是下降的。这说明全省各个煤矿的安全生产观念逐渐增强，安全形势不断提高。

灰色系统理论建立的GM(1，1)预测模型适合百万吨死亡率的预测，模型具有完整严密的理论系统和科学的分析计算方法，其相关预测精度和符合要求，因此预测结果可靠，达到了建立该模型的目的，对煤矿的安全管理有指导意义。

3 结论

1)灰色系统预测模型借助于历史数据对未来数据进行预测，其预测准确度符合要求，能客观地体现出煤矿百万吨死亡率的现实规律，反映现阶段煤矿企业的安全状况，因而具有很强的现实使用价值。

2)灰色预测系统的数学模型简单易于建立，要求的原始数据较少，实现了利用离散的数据序列建立连续的动态微分方程的飞跃，为安全管理提供了指导。

3)煤矿的百万吨死亡率在未来几年甚至几十年不可能无限制地递减至0，受诸多因素的影响，在达到一定数值之后，将有可能会出现非常慢的递减变化甚至停滞，也可能会出现小幅度的回升现象，正如本文中的2012年山西省煤矿百万吨死亡率比2011年的有所回升。因此，每间隔一段时间，必须删除冗余信息，补充新信息，重新建立或修正预测模型，保证预测的科学可靠性。

［1］赵红梅，陈开岩.关于我国煤矿百万吨死亡率的灰色预测探讨［J］.矿业安全与环保，2006，33(4):77－79.

［2］金龙哲，宋存义.安全科学原理［M］.北京:化学工业出版社，2004:64－66.

［3］李润求，施式亮.基于灰色系统理论的煤矿安全生产形势预测［J］.矿业工程研究，2010，25(3):54－57.

［4］叶加冕.某矿山事故伤亡率的灰色预测［J］.矿业快报，2004，(8):12 －13..

［5］江成玉，李春辉，苏恒瑜.基于GM(1，1)模型的煤矿百万吨死亡率的预测研究［J］.煤炭技术，2010，29(4):81－82.

［6］吕贵春，马云东.矿井瓦斯涌出量预测的灰色建模法［J］.中国安全科学学报，2004，14(10).

［7］刘思峰，谢乃明.灰色系统理论及其应用［M］.北京:科学出版社，2008.

［8］杨瑞波，陈建宏.残差修正GM(1，1)模型在煤矿事故预测中的应用［J］.矿业研究与开发，2011，31(1):73－76.

［9］周晓明，罗文柯.改进GM(1，1)预测模型对我国煤炭消费需求的预测分析［J］.矿业工程研究，2010，25(2):65－68.

［10］兰建义，周英.基于改进灰色GM(1，1)马尔柯夫模型的煤矿事故百万吨死亡率预测［J］.数学的实践与认识，2014，33(17):145 －152.

［11］康向涛，刘勇.关于贵州煤矿百万吨死亡率灰色预测的探讨［J］.煤炭技术，2011，30(7):246－248.

［12］康向涛，刘勇.灰色预测在贵州煤矿安全生产中的应用［J］. 煤炭技术，2011，30(6):115－117.