压力变化对Ⅰ型甲烷水合物稳定性影响的分子动力学模拟

段小龙，任 红，高光海，许俊良，仇性启

（1.中国石油大学（华东）化学工程学院，山东 青岛 266580；2.中国石化 胜利石油管理局钻井工艺研究院，山东 东营 257017）

气体水合物是水与甲烷、乙烷、CO2和H2S等小分子气体在高压、低温环境中形成的非化学计量性的笼状晶体物质。空的水合物晶格就像一个高效的分子水平的气体存储器，每立方米水合物可储存160～180 m3天然气［1］。随着世界油气资源的日益枯竭，天然气水合物作为人类的潜在能源在世界范围内受到高度重视。

近年来，国内外研究人员针对水合物开展了大量实验和理论研究，水合物在微观水平的成核机制、分解机制以及抑制剂对水合物生成及分解的影响机理是目前的研究热点［2］。基于经验势的分子动力学模拟是研究水合物的有效方法［3-5］，Saruprias等［6］用分子动力学模拟CO2水合物的分解过程，指出客体分子晶穴占据率和温度效应是影响水合物稳定性的重要因素；Roger［7］用分子动力学方法研究了客体分子对水合物稳定性的影响；丁丽颖等［8-9］对Ⅰ型甲烷水合物的稳定性进行了分子动力学研究，测试了不同温度及客体分子占据率下甲烷水合物的稳定性，提出了判断水合物稳定性的依据；Takeshi等［10］模拟了客体分子晶穴占据率对水合物稳定性的影响规律。目前，采用分子动力学方法研究水合物稳定性主要集中在温度、客体分子及其晶穴占据率等方面，对压力条件的影响研究较少。

本工作采用分子动力学方法研究了压力变化对Ⅰ型甲烷水合物稳定性的影响规律，对体系构象、径向分布函数、势能变化及均方位移等参数进行了分析，从微观角度揭示了水合物降压分解机理。

1 计算模型

1.1 模拟体系

采用Ⅰ型甲烷水合物的2×2×2超晶胞作为模拟体系（如图1所示），在x，y，z 3个坐标方向上使用周期性边界条件，控制晶胞尺寸为2.452 nm×2.452 nm×2.452 nm，体系包含368个水分子和64个甲烷分子。采用文献［11］报道的方法搭建Ⅰ型水合物笼状孔穴结构，氧原子初始位置根据X单晶衍射实验［12-13］结果确定，晶格中氢原子按无序性排列，使其满足Bernal-Fowler规则［14］。

1.2 计算方法

模拟在Materials Studio平台下进行，采用NPT系综，选用相容化合价力场［15］，使用Ewald加和法计算范德瓦尔斯相互作用和长程静电相互作用，并分别采用Nose热溶方法和Berendsen方法控制体系的温度和压力。本工作使用Lennard-Jones势能函数描述甲烷分子与水分子之间以及甲烷分子之间的相互作用；采用简单点电荷势能模型控制水分子之间的相互作用，将水分子视为刚体分子，其键长与键角固定。在进行分子动力学模拟前，先用最速下降法和共轭梯度法对体系结构进行几何优化，使体系的初始结构处于能量最小状态。模拟过程的时间步长取1 fs，每个温压点的模拟时长取1 ns。

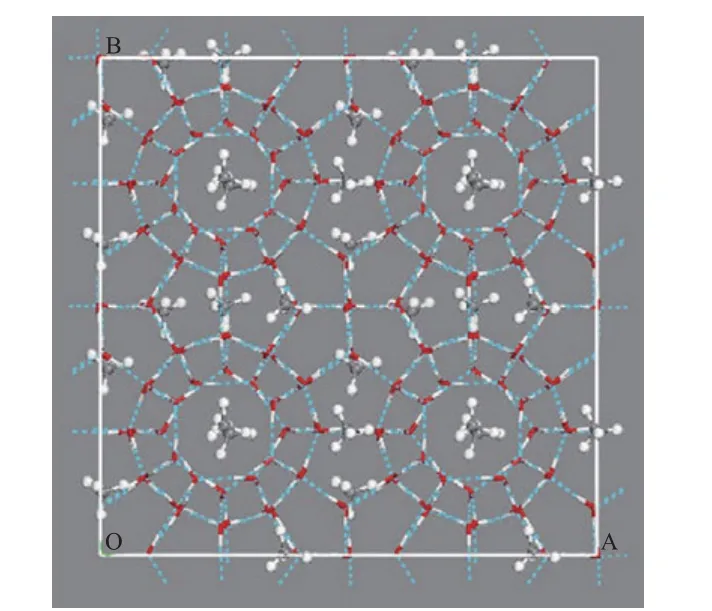
图1 Ⅰ型甲烷水合物的初始构象Fig.1 Initial structure of SI methane hydrate.

本工作主要对温度为280 K、晶格占据率为1、压力分别为10，20，30，40 MPa下的Ⅰ型甲烷水合物体系进行分子动力学模拟，分析不同压力条件下体系构象、径向分布函数、体系势能和均方位移等参数的变化，并总结出相关规律。

2 结果与讨论

2.1 体系构象分析

对Ⅰ型甲烷水合物超晶胞体系进行分子动力学模拟，得到不同压力下体系的最终构象结果如图2所示。

图2 不同压力下体系的最终构象Fig.2 Final structures of the mathane hydrate under different pressure.

由图2可看出，压力分别为40 MPa和30 MPa时，水分子基本保持有序性排列，由水分子构成的笼状孔穴结构仅出现轻微的变形；压力为20 MPa时，水合物的笼状孔穴结构变形程度较严重，同时少量的甲烷分子从笼状孔穴中逸出并出现聚集倾向；当压力降至10 MPa时，由水分子构成的有序晶体结构已经不存在，甲烷分子聚集在一起，体系呈气液两相分离的状态。

图3展示了10 MPa、280 K条件下，由水分子组成的笼状孔穴结构的解离过程。由图3可见，当模拟进行至50 ps时，笼状孔穴结构发生轻微变形，但基本保持稳定；随着模拟的进行（50～120 ps），水分子扩散加剧，笼状孔穴结构破裂开口，封存在笼状孔穴结构内的甲烷分子逸出，成为自由分子。

图3 笼状孔穴结构的变化Fig.3 Structural change of the hydrate cage.p=10 MPa.

2.2 径向分布函数

径向分布函数是衡量凝聚态物质有序性的重要参数。水分子中的氧原子和甲烷分子中的碳原子的径向分布函数分别见图4和图5。由图4可看出，氧原子的径向分布函数分别在0.275 nm和0.450 nm处出现两个特征峰：第一特征峰代表以氢键相连的两个氧原子之间的距离，即笼状结构中五边形的边长；第二特征峰代表水合物中相隔一个或多个水分子的氧原子的距离。这与文献［16-17］报道的结果一致。

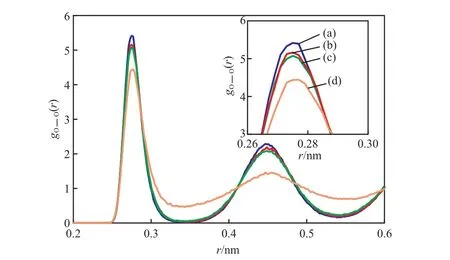
图4 氧原子的径向分布函数Fig.4 Radial distribution functions of oxygen atom(gO—O(r))under different pressure.

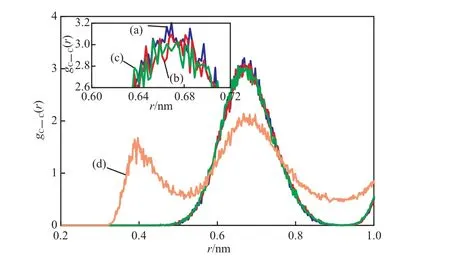
图5 碳原子的径向分布函数Fig.5 Radial distribution functions of carbon atom(gC—C(r))under different pressure.

随着压力的下降，氧原子径向分布函数特征峰展宽变宽，峰值减小，说明甲烷水合物中水分子排列的有序性降低，晶体结构受到破坏；当体系压力为40，30，20 MPa时，氧原子径向分布函数的特征峰值较接近，这是由于体系压力较高，水合物中的笼状孔穴结构尚未解离，水分子依然呈有序性排列；当体系压力降至10 MPa时，径向分布函数特征峰高度下降程度最为明显，说明水合物笼状孔穴结构被破坏，水合物晶体结构逐渐分解。

由图5可以看出，体系压力为40，30，20 MPa时，碳原子的径向分布函数在0.690 nm处出现第一特征峰值，代表了两个笼状孔穴中碳原子之间的距离［17］，说明此时水合物笼状孔穴结构稳定，甲烷分子分别处于各自笼状的孔穴中；而当压力降至10 MPa时，碳原子径向分布函数第一特征峰值移至0.410 nm处，代表甲烷分子从笼状孔穴中逸出并聚集后的碳原子之间的距离。

图6为模拟过程中不同时段的碳原子径向分布函数。由图6可看出，碳原子的径向分布函数在最初阶段（0～50 ps）只在0.680 nm处有一特征峰值，此时水合物保持稳定状态，甲烷分子处于笼状孔穴中；在模拟的中间阶段（50～120 ps），在0.410 nm处开始出现另一特征峰值，两个特征峰值并存，且随着模拟的进行，0.410 nm处的特征峰值逐渐升高，0.680 nm处的特征峰值逐渐下降，说明笼状孔穴结构正在逐步解离，甲烷分子逸出孔穴并发生聚集；在模拟的最后阶段（120～1 000 ps），0.680 nm处的特征峰值消失，只在0.410 nm处存在一个特征峰值，此时水合物已彻底分解，所有甲烷分子聚集在一起。

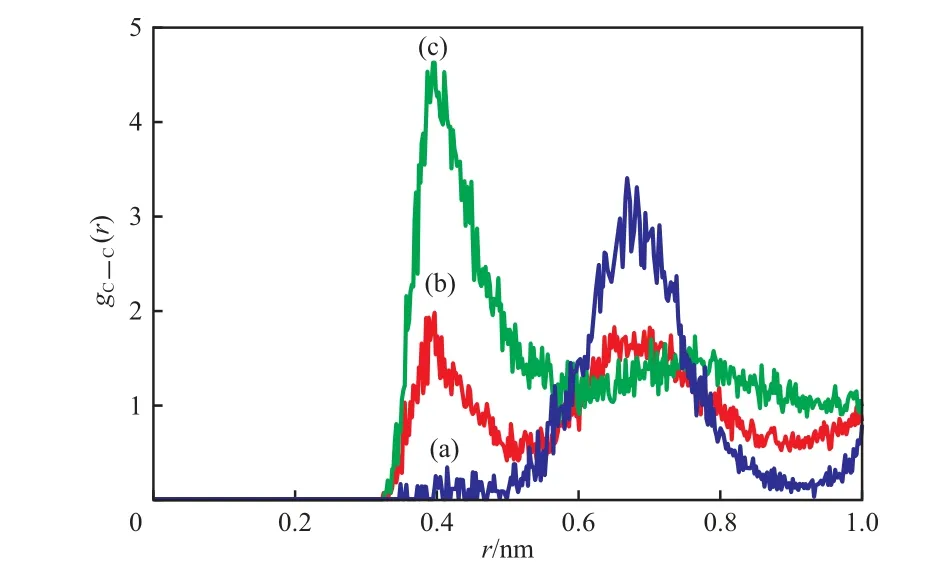
图6 不同模拟时段碳原子的径向分布函数Fig.6 Radial distribution functions of carbon atom in different time interval(t).

2.3 势能变化

模拟过程中体系的势能变化见图7。由图7可见，体系势能在各个压力下都能达到平衡，且压力越低，体系越不稳定，势能越大。当体系压力较高（40，30，20 MPa）时，势能在某一位置波动，表明在此条件下体系具有稳定的晶体结构，水分子和甲烷分子在各自的平衡位置振动和转动，水合物未发生分解。当压力降至10 MPa时，0～100 ps内随着模拟的进行，势能在缓慢增加，结合2.1节中对体系构象的分析，这是因为此阶段笼状孔穴结构正在解离，水分子排列由有序变为无序；固相水合物完全分解为气液两相后，势能不再增加，最终稳定在某一位置波动。

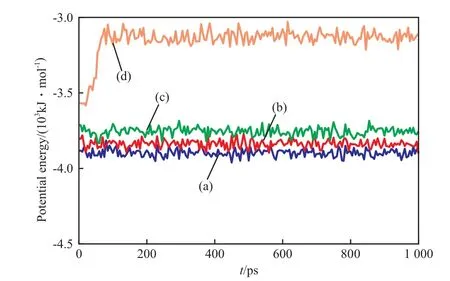
图7 体系的势能变化Fig.7 Potential energy change of the system.

2.4 均方位移

均方位移反映了体系中的粒子在分子动力学模拟过程中空间位置与其初始位置的偏离程度。图8和图9分别为不同压力下水分子中氧原子和甲烷分子中碳原子的均方位移随时间的变化曲线。从图8和图9可看出，随压力的下降，氧原子和碳原子的均方位移均增大；当压力为40，30，20 MPa时，氧原子和碳原子的均方位移均上升至略大于零的数值后趋于稳定，这表明水分子在固定的位置发生微小振动，体系具有稳定的晶格结构；而压力降至10 MPa后，随着模拟的进行，氧原子和碳原子的均方位移均逐渐增加，且均方位移增长的变化率随时间的延长而逐渐增大，在最后阶段（700～1 000 ps）均方位移曲线均趋于一条直线。气体分子和液体分子在扩散过程中其均方位移与时间呈线性关系［18］，这表明甲烷水合物经历了笼状孔穴结构破裂、甲烷分子逸出并最终分解为气液两相的过程。

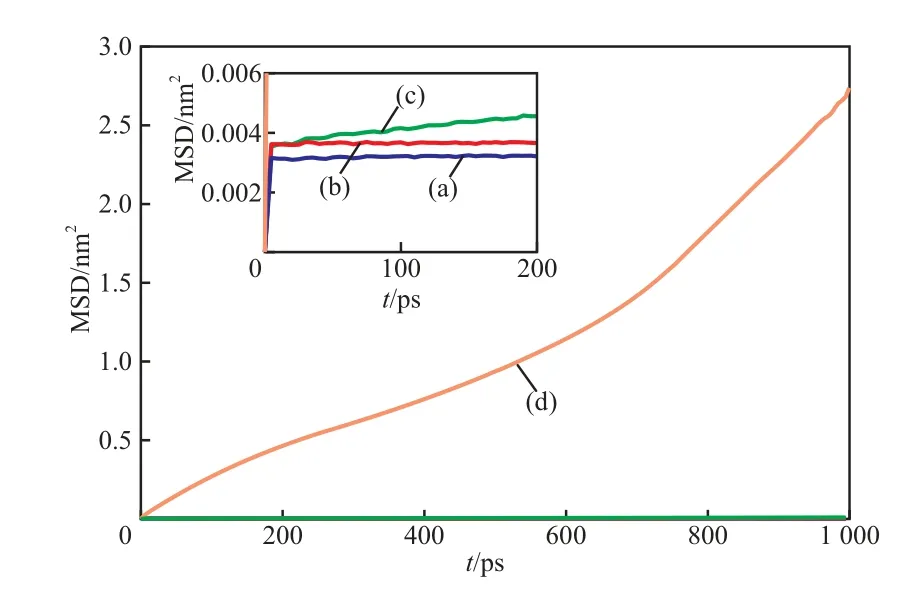
图8 不同压力下氧原子的均方位移Fig.8 MSD of oxygen atom under different pressure.

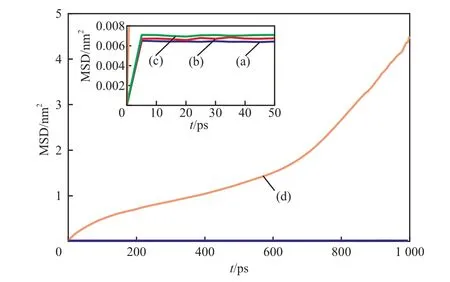
图9 不同压力下碳原子的均方位移Fig.9 Mean square displacement(MSD) of carbon atom under different pressure.

3 结论

1）体系压力越低，稳定后的势能越大，体系越不稳定。

2）随压力的降低，氧原子径向分布函数特征峰值减小，展宽变宽，水分子排列有序性下降。

3）体系压力为40，30，20 MPa时，氧原子和碳原子的均方位移稳定在略大于零的某一数值，体系较稳定；当压力降至10 MPa时，均方位移急剧增大，在最后阶段（700～1 000 ps）曲线趋于一条直线。

4）通过对体系构象、势能变化、径向分布函数及均方位移等参数进行分析，从微观角度揭示了Ⅰ型甲烷水合物降压分解机理：随体系压力的降低，由水分子以氢键连接形成的笼状孔穴结构变形并逐渐解离，甲烷分子从笼状孔穴结构中逸出并聚集，固相水合物最终分解为气液两相。

［1］陈光进，孙长宇，马庆兰.气体水合物科学与技术［M］.北京：化学工业出版社，2007：305-309.

［2］刘源.气体水合物分子间相互作用及分解行为的理论研究［D］.大连：大连理工大学.2012.

［3］Brodholt J，Wood B.Molecular-Dynamics Simulations of the Properties of CO2-H2O Mixtures at High-Pressure and Temperatures［J］.Am Mineral，1993，78（5/6）：558-564.

［4］Yan Kefeng，Mi Jianguo，Zhong Chongli.Molecular Dynamics Simulation of Inhibiting Effects on Natural Gas Hydrate［J］.Acta Chim Sin，2006，64（3）：223-228.

［5］梅东海，李以圭，陆九芳，等.H型甲烷水合物结构稳定性的分子动力学模拟［J］.化工学报，1998，49（8）：662-670.

［6］Saruprias S，Debenedetti P G.Molecular Dynamics Study of Carbon Dioxide Hydrate Dissociation［J］.J Phys Chem A，2009，113（10）：1913-1921.

［7］Roger P M.Stability of Gas Hydrate［J］.J Phys Chem，1990，94（15）： 6080-6089.

［8］丁丽颖，耿春宇，赵月红.Ⅰ型甲烷水合物晶体稳定性的分子动力学模拟［J］.计算机与应用化学，2007，24（5）：569-574.

［9］Ding Liying，Geng Chunyu，Zhao Yuehong，et al.Molecular Dynamics Simulation on the Dissociation Process of Methane Hydrates［J］.Mol Simulat，2007，33（12）：1005-1016.

［10］Takeshi Sugahara，Hiroki Mori，Jun Sakamoto，et al.Cage Occupancy of Hydrogen in Carbon Dioxide，Ethane，Cyclopropane，and Propane Hydrates［J］.Open Therm J，2008（2）：1-6.

［11］Storr M T，Taylor P C，Monfort J P，et al.Kinetic Inhibitor of Hydrate Crystallization［J］.J Am Chem Soc，2004，126（5）：1569-1576.

［12］Rawn C J，Rondinone A J，Chakoumakos B C，et al.Neutron Powder Diffraction Studies as a Function of Temperature of Structure Ⅱ Hydrate Formed from Propane［J］.Can J Phys，2003，81（1/2）：431-438.

［13］Gutt C，Asnussen B，Press W，et al.The Structure of Deuterated Methane-Hydrate［J］.J Chem Phys，2000，113（11）： 4713-4721.

［14］Greathouse J A，Cygan R T，Simmons B A.Vibrational Spectra of Methane Clathrate Hydrates from Molecular Dynamics Simulation［J］.J Phys Chem B，2006，110（13）：6428-6431.

［15］Geng Cunyu，Wen Hao，Zhou Han.Molecular Simulation of the Potential of Methane Reoccupation During the Replacement of Methane Hydrate by CO2［J］.J Phys Chem A，2009，113（18）：5463-5469.

［16］Ota M，Ferdows M.Monte Carlo Approach to Structure and Thermodynamic Property of CO2Hydrate［J］.JSME Int J B，2005，48（4）：802-809.

［17］万丽华，颜克凤，李小森，等.热力学抑制剂作用下甲烷水合物分解过程的分子动力学模拟［J］.物理化学学报，2009，25（3）：486-494.

［18］陈正隆，徐为人，汤立达.分子模拟的理论与实践［M］.北京：化学工业出版社，2007：112-114.