太阳帆柔性结构动力学仿真分析*
2014-05-02郑建华
马 鑫,杨 萱,郑建华,2,杨 华
(1.中国科学院空间科学与应用研究中心,北京100190;2.航天飞行动力学技术重点实验室,北京100094;3.中国科学院大学,北京100190;4.内蒙古电子信息职业技术学院,呼和浩特010011)
0 引 言
现代航天器大多采用推进系统来获得推力.随着航天飞行任务距离增加和运行时间增长,其必然要携带越来越多的燃料,进而提高航天器发射成本,这就使得依靠光压作为动力的太阳帆航天器应运而生[1].利用太阳光的持续作用力,完成一些过去无法实现的任务[2].太阳帆帆面采用超轻质聚酰亚胺薄膜[3],由于太阳光压非常小,所以其面积一般为上千平方米左右.太阳帆航天器一般需要很长的伸展支撑构件来引导太阳帆帆面展开[4].帆面与支撑臂决定了太阳帆航天器结构的大柔性特点,为了确保航天器姿态稳定性和指向精度的要求,必须搞清这类复杂航天器的柔性结构动力学特征[5-6].
太阳帆的动力学建模仿真工作十分关键,Wie[7]对边长20m的方形太阳帆建立了有限元模型,着重考虑了析架式伸展臂弯曲与扭转对帆面模态的影响;张锦等[8-9]利用Abaqus软件对边长为148m的方形太阳帆建立了有限元模型,分析了其在飞行轨道引力、太阳光压、控制力矩的载荷边界条件下的模态频率;郭红军等[10]运用Ansys软件分析了方形太阳帆平行与垂直太阳光两种飞行姿态下的前8阶模态频率.本文考虑帆面被伸展臂拉紧而受到预紧力作用,利用Nastran有限元软件给出太阳帆航天器的一种整体有限元模型,进行帆面模态与伸展臂屈曲分析,并与帆面无预紧力的工况进行比较,为航天器控制系统设计提供了重要的设计参数.
1 有限元模型
在太阳帆航天器中,有限元分析的难点在于对帆面与伸展臂联结点的真实模拟.表1~2为本文太阳帆帆面、伸展臂结构参数.

表1 帆面结构、材料参数Tab.1 The sail surface structure and material parameters

表2 伸展臂结构、材料参数Tab.2 The stretch arm structure and material parameters
对于太阳帆伸展臂结构,考虑其同时承受轴向拉压载荷与横向弯曲载荷,所以采用梁单元;对于帆面结构,由于实际中选用表层镀铝的聚酰亚胺超薄材料[3],所以采用膜单元模拟,并赋予膜单元三层复合材料单元属性;对于帆面与伸展臂联结点,为了更加贴近实际状态采用RBE2单元进行模拟,保证了帆面节点与伸展臂节点在三向位移坐标上的一致性,同时又不对3个转动自由度做任何约束;由于太阳帆航天器属于刚性体加柔性体结构,伸展臂、帆面作为挠性体对于结构模态特性起到决定性作用,所以将模型中心节点看做固定不动结构,将其6个自由度完全约束.太阳帆航天器有限元模型如图1所示.

图1 太阳帆航天器有限元模型Fig.1 The finite elementmodel of solar sail spacecraft
2 无预紧力载荷工况
本文认为太阳帆伸展臂与帆面联结点只存在联结关系,静态情形下不存在相互作用力.此种载荷工况要求帆面自身材料加工性能良好,可以在无需外力牵引的情况下保证自身帆面平整.此时,太阳帆航天器有限元整体模型只有模型中心节点固定不动这一个边界条件.
太阳帆帆面模型厚度仅为3.4μm,为非常规模型,由于帆面材料厚度与面积大小的最大比值远小于Nastran的默认值10-8,需要对Patran前处理提交计算的bdf文件进行修改,通过在其属性设置行加入“AUTOSPC(EPS=1.0e-13,EPSSING=1.0e-13)=YES”Damp语句,将其数量级扩大再提交Nastran计算[11].其一阶模态频率计算结果为9.1253×10-7Hz,振型图如图2所示(一阶模态振型为4片帆面依次显示,振型相同,这里只给出一片帆面即可).
由振型图可以看出,方形太阳帆航天器的大柔性主要体现在对称分布的4片柔性材料帆面结构上,太阳帆伸展臂振型位移相对于太阳帆振型位移基本为0.仿真结果显示,其前三阶模态频率数量级在10-6、10-7Hz量级,低于太阳帆姿态控制系统控制频率(10-4Hz)2~3个量级[12],不易于太阳帆姿态控制,需要改进帆面材料性能提高帆面模态频率.通过增加聚酰亚胺薄膜或者镀铝涂层厚度,有望提高其模态频率,但是会带来太阳帆航天器整体质量的增加,从而增大发射成本.

图2 一阶模态振型图Fig.2 The firstmode
3 有预紧力载荷工况
在有预紧力载荷工况下,认为太阳帆伸展臂与帆面联结点不仅存在联结关系,而且它们之间存在相互作用力,即帆面被拉伸,在外力牵引下保证帆面张紧.此时,太阳帆航天器有限元整体模型除了模型中心节点固定不动的边界条件外,帆面角点也受到集中预紧力作用.
(1)预紧力分析
太阳帆帆面角点与伸展臂自由端端部相连,通过3个角点受预紧力作用,使帆面张紧.结合薄膜材料褶皱屈曲变形特点,要达到帆面张紧,要求帆面角点所受预紧力合力方向通过直角三角形帆面形[13],并且选取帆面应力值达到6~7kPa作为薄膜材料被拉紧的判断标准[13-14].
对四分之一帆面建立有限元模型,约束直角顶点6个自由度节点位移为0.在另外两个角点施加预紧集中力,通过加载不同的预紧力值,发现预紧力为1.31N时,帆面中部区域应力值为6540Pa,符合材料被拉紧应力条件.四分之一帆面有限元模型应力、应变云图如图3所示.

图3 四分之一帆面预紧力下应力、应变云图Fig.3 The stress and strain cloud of one-quarter sail surface
(2)模态分析
带有预紧力的有限元模态分析,需要采用冷启动运行SOL106方法,在提取特征值时,计算工况采用Automatic Givens方法,模态分析使用载荷步完成后最后的刚度矩阵[11].前三阶振型图如图4~6所示,模态分析结果如表3所示.

表3 前三阶模态分析结果Tab.3 The analysis results of the first threemodal

图4 一阶模态振型图Fig.4 The firstmode
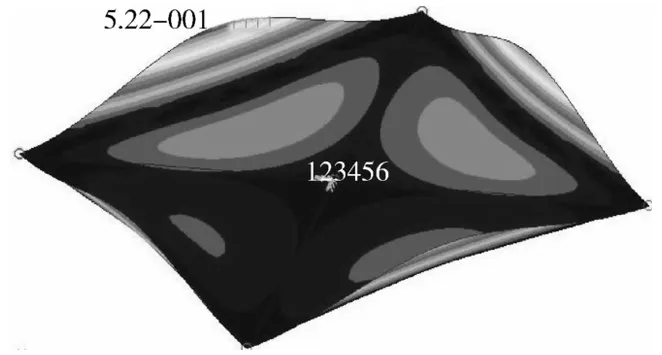
图5 二阶模态振型图Fig.5 The second mode

图6 三阶模态振型图Fig.6 The third mode
由振型图可以看出,有预紧力的方形太阳帆航天器的大柔性主要体现在对称分布的4片柔性材料帆面结构上,太阳帆伸展臂振型位移相对于太阳帆振型位移基本为0.仿真结果显示,其前三阶模态频率数量级在10-3Hz量级,高于太阳帆姿态控制系统控制频率10-4Hz一个量级[12],方便太阳帆姿态控制,在工程上具有实用价值.
(3)伸展臂屈曲校核
太阳帆航天器帆面由伸展臂展开并拉紧,伸展臂自由端端部会受到来自两个帆面角点预紧力合力的反作用力,即伸展臂受压,静态压力大小为2.34N,受压的伸展臂有可能在端部轴向载荷作用下发生失稳,从而影响帆面的展开效果.
对正方形对角线长度一半的伸展臂建立有限元模型,通过提取使线性系统刚度矩阵奇异的特征值来获取伸展臂结构的临界失稳载荷及失稳模态[15].采用Nastran中提供的SOL105计算方法进行屈曲分析,其一阶屈曲模态频率为5.8936Hz,振型图如图7所示,失稳临界载荷为特征值与施加的静态载荷的乘积,所以伸展臂最小失稳临界载荷为13.8N.

图7 伸展臂屈曲一阶模态振型图Fig.7 The firstmode of buckling analysis
分析结果表明,伸展臂在自由端端部承受2.34N轴向压力工况下,其屈曲模态基频远大于太阳帆航天器整体模型模态基频,不会与帆面共振而发生失稳;其屈曲模态基频远大于太阳帆姿态控制频率,不会与姿态控制发生共振而失稳;其最小失稳轴向载荷也大于端部轴向载荷,不会在轴向压力作用下失稳.
(4)优化拓展分析
通过以上对太阳帆航天器有预紧力工况下的完整仿真分析,可以提炼出一套基本思路,如图8所示.

图8 太阳帆航天器有预紧力分析基本思路Fig.8 The basic idea of the analysis for solar sail spacecraft with preload
在具体实际工程中,预紧力方向大小、模态频率、伸展臂屈曲这3个设计约束条件中任何一个或者多个都可以成为太阳帆航天器整体进行最优化设计的决定性条件,而另外的设计约束条件则要有所牺牲,不能达到最优值,要进行妥协设计.例如,对于本文中的工程模型,太阳帆航天器在预紧力10N以内的一阶模态频率值、帆面应力值如表4所示.

表4 预紧力10 N以内一阶模态频率值、帆面应力值Tab.4 The firstmode frequency and sail surface stress under 10 N preload
结果显示,太阳帆航天器结构模态基频(一阶模态频率)随着预紧力的增加而增大,其趋势越来越有利于太阳帆航天器姿态控制;太阳帆帆面应力随着预紧力的增加而增大,在预紧力达到10N时,帆面应力大于帆面拉平应力值(6~7kPa),但是仍然远小于帆面屈服应力值(117MPa).可见,预紧力方向大小、结构模态这两个设计约束条件满足空间很大,但是根据伸展臂屈曲设计约束条件,伸展臂端部轴向载荷不能大于13.8N,即对应的预紧力不能大于7.7 N,可见伸展臂屈曲设计约束条件满足空间很小,成为太阳帆航天器整体设计最优化的决定性条件.
基于伸展臂屈曲设计约束条件对上面结果进行进一步优化,根据工程经验,取安全系数为2,即预紧力设为3.85 N,对其进行模态分析,其模态基频为0.004 850 9 Hz,一阶模态振型图如图9所示.分析结果显示,经过优化设计后的太阳帆航天器模态基频由预紧力为1.31 N下的0.002 875 2 Hz提高到0.004 850 9 Hz,提高68.7%.在伸展臂屈曲设计约束条件作为最优决定性条件,预紧力方向大小、结构模态两个设计约束条件作为辅助性条件的情况下,设计达到了最优化.

图9 一阶模态振型图Fig.9 The firstmode
经过以上分析,可以得出太阳帆航天器有预紧力条件下最优化设计的基本思路:首先,按照图8所示基本思路进行初步分析;其次,根据分析过程中的中间结果,判断预紧力方向大小、结构模态、伸展臂屈曲这3个设计约束条件的满足空间,找出设计最优的决定性条件(即满足空间最小的设计约束条件);最后,依据工程经验,给出最优决定性条件的合理取值,结合剩余设计约束条件完成最优化设计.
4 结 论
比较太阳帆航天器在无帆面预紧力与有帆面预紧力条件下的模态分析结果,可以得出帆面预紧力增大了帆面的整体刚度,使得太阳帆航天器整体结构模态基频大幅度提高,满足了太阳帆姿态控制频率对于结构模态频率的要求.根据本文的仿真分析结果,在帆面材料屈服强度、伸展臂屈曲失稳均满足的条件下,还可以依据具体姿态控制频率大小对预紧力进行调整,从而为太阳帆姿态控制方案提供结构保障与设计输入参数.
本文建立了合理的方形太阳帆航天器有限元模型,给出并比较了无帆面预紧力与有帆面预紧力两种载荷工况下的模态仿真分析结果;针对有帆面预紧力载荷工况进行了具体的预紧力大小、方向以及伸展臂屈曲校核分析,形成了一套基本的太阳帆帆面预紧力设计计算模态仿真分析方法,对实际工程应用具有一定参考价值.
[1]陈健,曹永,陈君.太阳帆推进技术研究现状及其关键技术分析[J].火箭推进,2006,32(5):37-42.CHEN J, CAO Y, CHEN J.Current status of solar sail propulsion and analysis of its key techniques[J].Journal of Rocket Propulsion, 2006,32(5):37-42.
[2]钱航,郑建华,于锡峥,等.太阳帆航天器悬浮轨道动力学与控制[J].空间科学学报,2013,33(4):458-464.QIAN H,ZHENG JH,YU X Z,et al.Dynamics and control of displaced orbits for solar sail spacecraft[J].Chinese Journal of Space Science,2013,33(4):458-464.
[3]刘彪,冀棉,杨士勇.太阳帆材料研究进展[J].宇航材料工艺,2013,43(4):24-28.LIU B,JIM,YANG SY.Recent progress on solar sail materials[J].Aerospace Materials&Technology,2013,43(4):24-28.
[4]沈自才,张帆,赵春晴.IKAROS太阳帆的关键技术分析与启示[J].航天器工程,2012,21(2):101-107.SHEN Z C,ZHANG F,ZHAO C Q.Key technology analysis and enlightenment of IKAROS solar sail[J].Spacecraft Engineering, 2012,21(2):101-107.
[5]AHMED A S.Flexible multibody dynamics:review of past and recent developments[J].Multibody System Dynam ics,1997(1):189-222.
[6]MEIROVITCH L,NELSON H D.High spin motion of a satellite containing elastic parts[J].Journal of Spacecraft and Rocket, 1966,13(11):1597-1602.
[7]WIE B.AOCS performance and stability validation for large,flexible solar sail spacecraft[R].AIAA 2005-3926,2005.
[8]ZHANG J.Coup led attitude-orbit control of flexible solar sail for displaced solar orbit[J].Journal of Spacecraft and Rockets, 2013, 50(3):675-685.
[9]LIQ.Reduced model for flexible solar sail dynamics[J].Journal of Spacecraft and Rockets, 2011, 48(3):446-453.
[10]郭红军,郑津津,沈连婠,等.新型太阳帆结构模态分析[J].机械与电子,2013(6):3-11.GUO H J,ZHENG J J,SHEN LW,et al.Modal analysis of a new solar sail[J].Machinery&Electronics,2013(6):3-11.
[11]田利思,李相辉,马越峰,等.MSC Nastran动力分析指南 [M].北京:中国水利水电出版社,2012:229-240.
[12]胡洁,杨萱.太阳帆航天器展开机构柔性动力学建模 [J].微计算机信息,2012,28(4):155-156.HU J,YANG X.Dynamic modeling of solar sail spacecraft deployment mechanism[J].Microcomputer Information,2012,28(4):155-156.
[13]SU X F,FRANK A, BARMAC T, et al.Wrinkling analysis of a Kapton square membrane under tensile loading[R].AIAA 2003-1985,2003.
[14]王长国,杜星文,赫晓东.空间充气薄膜结构的褶皱分析[J].力学学报,2008,40(3):331-338.WANG C G,DU X W,HE X D.Wrinkling analysis of space inflatable membrane structures[J].Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(3):331-338.
[15]李邦国,路华鹏,胡仁喜,等.Patran2006与 Nastran2007有限元分析实例指导教程 [M].北京:机械工业出版社,2008:12-20.
