欠驱动三轴稳定卫星的消旋和进动控制技术
2014-05-02王新民张俊玲高益军徐福祥
王新民,张俊玲,袁 军,高益军,徐福祥
(1.北京控制工程研究所,北京100190;2.中国空间技术研究院,北京100094)
0 引 言
消旋和进动控制常常应用于自旋稳定卫星.许多早期的卫星都采用自旋稳定方式来稳定姿态.自旋稳定是利用卫星绕自旋轴旋转产生的动量矩在惯性空间的定轴性使自旋轴在无外力矩作用时在惯性空间定向,在有恒定外力矩作用时则以某角速度漂移而不是以加速度漂移,这种姿态稳定方式的优点是简单且抗干扰能力强[1].自旋稳定卫星一般设计有喷气推进系统,推力器的安装位置和自旋轴具有严格的几何关系[1-6],而且沿星体轴向、切向和径向3个方向分别配置推力器:轴向推力器产生自旋平面内的力矩,用于自旋轴进动即角动量方向控制;切向推力器用于控制转速即角动量大小(如启旋、消旋、转速保持等);径向推力器用于变轨.
三轴稳定卫星的喷气推进系统是一种主动式零动量姿态控制系统[1],推力器可以安装在星体任意位置和方向,只要考虑产生星体三轴方向的有效控制力矩,不需要考虑消旋和进动控制.一般将某方向推力器失效的卫星称为欠驱动卫星.如果需要将欠驱动三轴稳定卫星从高速自旋异常状态恢复到正常姿态,通常先进行消旋和进动控制,但是用来进行控制的推力器往往存在其他方向的多余分量,该分量没有其他推力器来抵消,此时的消旋和进动控制同样属于欠驱动.本文提出了一种欠驱动三轴稳定卫星的消旋和进动控制技术,给出了在轨验证结果.
1 消旋控制
1.1 控制原理
针对喷气控制力矩与消旋方向不一致的欠驱动卫星,如图1所示,假设自旋轴角动量H方向和喷气控制力矩Tjet方向的夹角为α,则Tjet与H平行的分量大小为

Tjet与H垂直的分量大小为

由此可见,如果采用“整数倍自旋周期全喷气”或“对称点喷”方式,则Tjet-Hs将累积而Tjet-Ht会抵消,这样引起的章动很小.当卫星有较好的章动阻尼时,经过适当次数的喷气,总能把卫星消旋控制到期望大小.如果推力器喷气时间为Δt,则喷气控制产生的自旋轴角动量变化为


图1 角动量和控制力矩关系示意图Fig.1 The angularmomentum and the control torque
1.2 实施步骤
消旋控制主要包括如下步骤.
(1)确定欠驱动卫星自旋轴和消旋控制的方向和大小
消旋控制前要分析卫星初始自旋轴的方向和大小,自旋轴的方向和大小是根据姿态敏感器确定的,如太阳敏感器,确定方法一般采用几何法或代数法[1,7-8].根据初始自旋轴和目标自旋轴的大小即可确定卫星的消旋控制方向和大小.
(2)确定进行消旋控制的推力器
如果推力器产生的力矩和消旋方向不一致,而且干扰力矩分量没有其他方向的推力器来控制,则属于欠驱动控制.一般根据姿态遥测数据确定,主要分析控制力矩和陀螺测量的响应是否一致,即是否满足:
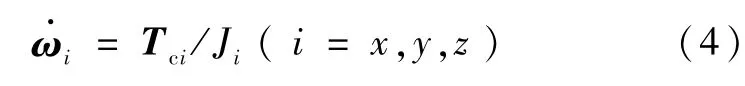
在欠驱动消旋控制的情况下,需要分析可以用来进行消旋控制的推力器产生的力矩大小和方向,及其与消旋方向的几何关系.选取消旋控制分量大的推力器,即选取喷气控制力矩在消旋控制方向上分量最大的喷气控制推力器作为欠驱动消旋控制的推力器.
(3)欠驱动消旋控制
对于喷气控制力矩与消旋方向不一致的欠驱动卫星,需要利用力矩分量进行消旋控制,可采用星上自主闭环模式也可采用地面遥控的开环模式.为了提高效率,一般在消旋初期采用“整数倍自旋周期全喷气”方式,在消旋末期(接近目标)则采用“对称点喷”方式.
“整数倍自旋周期全喷气”方式不难实现,即喷气时间为mTs,其中Ts为卫星自旋周期,m为整数.“对称点喷”方式则是在一个周期内喷气2N次,其中N为整数,从调整所在的卫星自旋周期的起始时刻开始计时,在每隔Ts/(2N)时刻使用消旋控制推力器喷一个持续时间为ΔtN的脉冲:
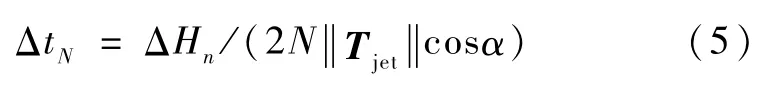
其中ΔHn为本次消旋角动量大小.为了减小产生的章动,一次消旋完成后,应使星体自然阻尼一段时间(一般至少取1个自旋周期),衰减本次控制带来的章动,之后进行下次的消旋控制.
以利用数字太阳敏感器信息进行星上自主的消旋控制为例,消旋控制的基本策略如下:
1)根据数字太阳敏感器的测量数据确定卫星的自旋轴和自旋周期Ts.
2)在消旋初期采用“整数倍自旋周期全喷气”方式,在t0时刻开始进行消旋控制,推力器喷气时间为mTs.控制完成后监测卫星状态.间隔1个周期再进行下一次喷气控制.
3)在消旋末期采用“对称点喷”方式,在t0+时刻进行消旋控制,k表示一个自旋周期内的喷气次序,每次喷气时间为
4)计算卫星自转轴与太阳矢量的夹角和卫星自转周期.
5)t0为喷气基准时间,根据数字太阳敏感器测量输出过0的时间确定.N由喷气控制次数确定,章动自主衰减快,N可取大些.
图2为一个自旋周期进行4次消旋控制的“对称点喷”方式示意图,阴影区域表示喷气弧段,此时进行消旋控制.

图2 “对称点喷”方式示意图Fig.2 Symmetry phase little-pulse firing mode
2 进动控制
2.1 控制原理
针对喷气控制力矩与进动方向不一致的欠驱动卫星,如图3所示,假设初始自旋轴角动量H方向和喷气控制力矩Tjet方向的夹角为β,则Tjet与H平行的分量大小为

Tjet与H垂直的分量大小为

假定初始时刻卫星处于纯自旋状态,自旋速度大小为ωs,即卫星的角动量和自旋轴重合,则在卫星旋转到某相位角的Tp/2前后时间内进行喷气控制,其中Tp为喷气脉冲时间宽度,如图4阴影部分所示,产生的进动角动量增量为

由此可见,如果采用脉冲调制方式进行喷气且喷气弧段极短,则
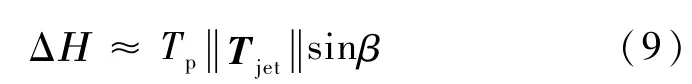
此时引起的章动角很小,当卫星有较好的章动阻尼时,经过适当次数的脉冲喷气,总可以把卫星自旋轴方向进动控制到期望方向.

图3 进动控制和喷气控制力矩关系示意图Fig.3 Precession control and the jet control torque

图4 进动控制相位示意图Fig.4 Phase of precession control
单次控制脉冲宽度Tp根据本次预备控制的进动角动量增量和控制的相对误差η=等关系确定,工程上一般取为喷气弧段阈值,即且满足

最后一次喷气前喷气时间长度均可小于或等于δ/ωs,如果δ取0.7,则η<0.02,即进动控制的相对误差在2%内.
2.2 实施步骤
进动控制主要包括如下步骤.
(1)确定欠驱动卫星自旋轴和进动控制的方向和大小
卫星进动控制前要分析卫星初始自旋轴的方向和大小,确定方法与消旋控制确定自旋轴的方法相同.根据初始自旋轴和目标自旋轴的方向即可确定卫星的进动控制方向和大小.
(2)确定进行进动控制的推力器
一般根据姿态遥测数据确定.主要分析控制力矩和陀螺测量的响应是否一致.在欠驱动进动控制的情况下,需要分析可以用来进行进动控制的推力器产生的力矩大小和方向,及其和进动方向的几何关系.选取进动控制分量大的推力器,即选取喷气控制力矩在进动控制方向上分量最大的喷气控制推力器作为进动控制推力器.
(3)欠驱动进动控制
对于喷气控制力矩与进动方向不一致的欠驱动卫星,需要利用力矩分量进行进动控制,可以采用星上自主闭环模式也可以采用地面遥控的开环模式.为了减小产生的章动,采用脉冲调制方式且喷气弧段极短,一次进动完成后,应使星体自然阻尼一段时间(一般至少取1个自旋周期),衰减本次控制的章动角度,之后才可以进行下次的进动控制.
以利用数字太阳敏感器信息进行星上自主的进动控制为例,进动控制的基本策略如下:
1)根据数字太阳敏感器的测量数据确定卫星自旋周期Ts、喷气基准时刻t0.
3)计算卫星自转轴与太阳矢量的夹角和卫星自转周期.
4)Ts和t0的确定方法和喷气时序如图5所示.图中斜线表示数字太阳敏感器的测量输出,从负角度斜向上直至输出正角度,图中的横轴表示输出为0,连续两次过0的时间,即经过了一个自旋周期Ts,数字太阳敏感器的测量输出从负变正的时刻计为喷气基准时刻t0,F-P为时序计数器,F-P=3的阴影区域表示喷气弧段,此时进行进动控制.Tp、t0和Ts均可以自主确定和自调整.
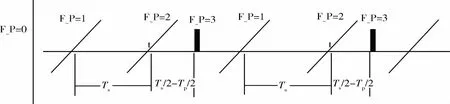
图5 进动控制时序示意图Fig.5 Time sequence of precession control
3 在轨验证情况
某卫星丢失姿态后,在不同阶段采用上述多种喷气控制方法进行了欠驱动消旋和进动控制,执行机构为喷气控制力矩在消旋、进动控制方向上分量最大的推力器,将卫星从高速自旋异常状态控制到陀螺退饱和,实现了卫星减速同时保证了能源安全,建立了恢复正常姿态的条件.
卫星采用“整数倍自旋周期全喷气”方式利用欠驱动推力器进行消旋控制,将卫星自旋速度由36(°)/s降低到19.2(°)/s,控制前后整星电源输出情况曲线见图6~7,卫星采用数字太阳敏感器信息利用欠驱动推力器进行自主进动控制,将卫星自旋轴与太阳矢量夹角从97°降低到25°,控制前后整星电源输出情况曲线见图8~9,从整星电源输出电流可以看出,消旋或进动控制后效果显著,整星能源得到保障.根据在轨表现,卫星最长经过一个轨道圈就基本自然消除了每次消旋或进动喷气控制引起的章动现象.

图6 消旋控制前整星电源输出情况Fig.6 Power output before despinning control

图7 消旋控制后整星电源输出情况Fig.7 Power output after despinning control

图8 进动控制前整星电源输出情况Fig.8 Power output before precession control
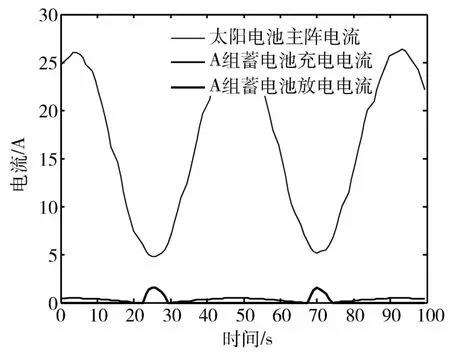
图9 进动控制后整星电源输出情况Fig.9 Power output after precession control
4 结 论
本文给出了一种欠驱动三轴稳定卫星从高速自旋异常状态恢复到正常姿态期间进行欠驱动消旋和进动控制的方法,在轨验证了该方法的正确性,该方法可以推广到任何卫星,为航天器的长寿命运行提供了一种有效手段.
5 致 谢
在技术研究和在轨试验过程中,许多领导、专家和同事,如张笃周、袁利、宗红、何英姿、魏春岭、陈义庆、李铁寿、雷拥军、王淑一、田科丰、赵性颂、周剑敏等,提出了许多有价值的思路和建议,在此一并致以衷心的感谢.
[1]屠善澄.卫星姿态动力学与控制[M].北京:宇航出版社,2001:121-164.
[2]章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,1998:185-238.
[3]VLADIMIR A C.Spacecraft attitude dynamics and control[M].Florida:Malabar Krieger Publishing Company,1991:17-23.
[4]FRAUENHOLZ R B.Maneuver reconstruction techniques for open-loop spin-stabilized spacecraft[J].Journal of Guidance Control and Dynamics, 1982, 5(3):270-277.
[5]LEBSOCK K L, MCENNAN J J, MURPHY J R.Despin through unity inertia ratio[J].The Journal of the Astronautical Sciences, 1982, 30(3):213-228.
[6]MYUNG H S,BANG H.Predictive nutation and spin inversion control of spin-stabilized spacecraft[J].Journal of Spacecraft and Rockets, 2010, 47(6):1010-1022.
[7]van der HA J C.Spin-axis attitude determination using in-flight data[J].Journal of Guidance, Control, and Dynamics, 2010, 33(3):768-781.
[8]TANYGIN S,SHUSTER M D.Spin-axis attitude estimation[J].The Journal of the Astronautical Sciences,2007,55(1):107-139.
