星敏感器低频误差在轨校准方法研究*
2014-05-02熊凯,宗红,汤亮
熊 凯,宗 红,汤 亮
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
0 引 言
高分辨率对地观测要求对星上有效载荷进行精确的指向控制,或通过卫星姿态确定系统获取有效载荷光轴指向信息.在星上姿态确定系统中,由星敏感器和陀螺构成的星光惯性姿态确定(SIAD,stellar intertial attitude determination)系统精度较高.是众多航天任务的首选[1].
星光惯性姿态确定系统的性能依赖于星敏感器的精度,而星敏感器观测量中通常包含低频误差.星敏感器低频误差主要是由于太阳照射角度变化产生的冷热交变的热环境,使得星敏感器本体及其安装结构形变造成的.由于太阳照射角度依轨道周期变化,星敏感器低频误差可视为周期信号,其变化周期近似等于卫星轨道周期.据报导,在多个航天器上都发现了周期性的星敏感器低频误差的影响,如PROBA卫星、CHAMP卫星和ALOS卫星等[2-4].传统的姿态确定卡尔曼滤波算法未考虑星敏感器低频误差的影响,很难直接利用卡尔曼滤波消除星敏感器低频误差.存在星敏感器低频误差的情况下,将会导致卫星姿态确定精度降低.
文献[5]中给出了一种星敏感器低频误差校准方法.该方法中,将低频误差建模为一阶高斯-马尔可夫过程,并将其于卫星姿态和陀螺漂移一起进行估计.该方法的不足之处在于对陀螺测量精度的要求非常高.在以往工作中,曾提出一种基于多模型自适应估计(MMAE,multiple model adaptive estimation)的星敏感器低频误差校准方法,其基本思路是采用MMAE算法,利用陀螺漂移估计值的频谱对低频误差参数进行估计[6],该方法的局限性在于MMAE算法复杂,计算量较大,不利于在轨应用.
本文研究一种适合工程应用的星敏感器低频误差在轨校准方法,基本思路是将星敏感器低频误差参数扩充为状态,将卫星姿态运动学模型和低频误差数学模型相结合,用于建立误差校准模型,在此基础上设计扩维卡尔曼滤波(A-KF),同时对卫星姿态、陀螺漂移和星敏感器低频误差参数进行估计.与文献[5]中的方法不同,星敏感器低频误差被建模为傅里叶级数,而不是高斯-马尔可夫过程,通过AKF估计傅里叶级数的系数,而不是低频误差本身.与文献[6]中给出的基于MMAE的方法相比,基于A-KF的校准方法的优势在于计算量小,原理直观,更易于在轨实现.此外,本文分析了基于A-KF的校准方法的性能,指出低频误差校准方法的有效性与低频误差的幅度大小有关,相关内容在以往的工作中并未揭示出来.
1 低频误差校准方法
KF(Kalman filter)是基于系统模型设计的.对于卫星姿态确定系统模型而言,状态量由误差四元数和陀螺漂移误差构成,其表达式如下:
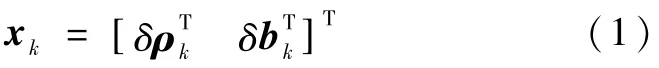
基于前面所定义的状态,离散形式的状态方程可以写为如下所示的线性形式:

式中

式中,wk是系统噪声向量,通常假定为0均值随机变量,其方差为

式中,Qk是已知正定矩阵.在状态转移矩阵Fk中,τ表示时间步长,In×n表示n×n阶单位阵,0m×n表示m×n阶0矩阵,是星体角速率

卫星姿态确定系统的测量方程形式为

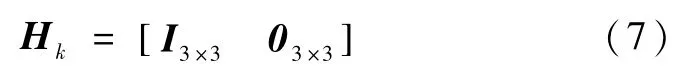
vk是测量噪声向量,通常假定为0均值随机变量,其方差阵为

式中,Rk是已知正定矩阵.表示星敏感器低频误差对观测量的影响.考虑到星敏感器低频误差可视为周期信号,并且其信号周期近似等于轨道周期,Δk的3个分量可建模为傅里叶级数的形式
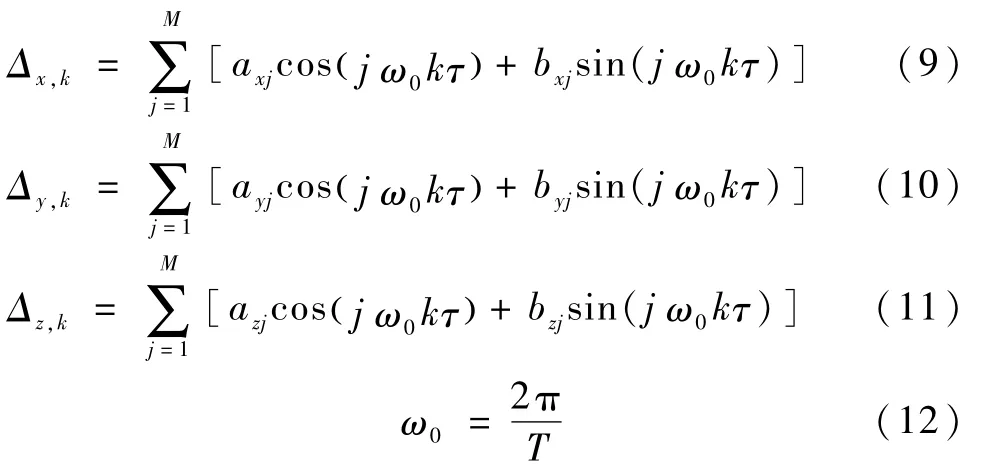
式中,T为卫星轨道周期,M为正常数,axj、bxj、ayj、byj、azj和bzj为未知的低频误差系数.
基于前述系统模型和观测模型,可以设计KF算法,用于处理观测量yk,获取状态量的最优估计.KF的标准形式如下所示:
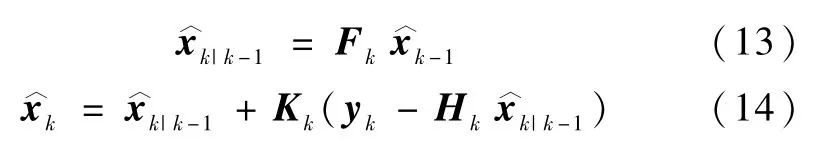
传统KF是在假设模型与实际系统相一致的情况下推导得到的,在模型与实际系统不一致,即存在模型不确定性的情况下,通过KF得到的状态估计不是最优的.这会导致估计得到的卫星姿态信息不准确.
为了削弱星敏感器低频误差的影响,提出一种基于A-KF低频误差校准方法.基本思路为:将低频误差参数扩充为状态,使得A-KF算法能够同时对卫星姿态和低频误差参数axj、bxj、ayj、byj、azj和bzj进行估计.本文仅考虑傅里叶级数的一阶项,也就是说,令M=1.此时,Δk可简写为
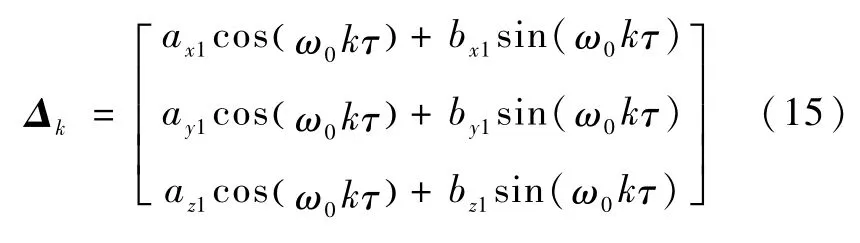
对于所设计的A-KF,扩维的状态中包括误差四元数、陀螺漂移误差和低频误差参数.此时,状态向量写为xk和θk的组合,即,其中,向量θk=[ax1bx1ay1by1az1bz1]T由低频误差校准参数组成.相应的,可构造得到如下形式的状态方程:

考虑到低频误差参数θk的变化非常缓慢,在几个轨道周期的校准过程中可以忽略不计向量θk的状态转移矩阵为6×6阶单位阵,相应的系统噪声设为0.
基于扩维的状态量,相应的观测方程可写为

其中,

针对如式(16)~(17)所示的系统,A-KF算法可写为

2 校准方法效能评估
本节通过理论推导分析低频误差校准对卫星姿态确定精度的影响,并对校准方法的应用提出一些建议.对于传统的姿态确定KF算法,估计误差定义为真实状态和估计状态之差,即

低频误差校准基于A-KF进行,A-KF的估计误差定义为
审计方式应当随着新型的神经网络技术的运用而作出一些调整,可以通过搭建审计数据的综合分析平台,从而建设和完善有关国家与人民的重点领域联网审计系统,对于一些半结构化、非结构化数据,我们可以通过一些专业工具的使用来对其进行处理,从而能够对一些规模较为庞大的数据信息进行高效地汇合和处理。如:在地税审计过程中,可通过地税联网审计系统,对全省得地税数据进行集中地整理分析,走出一条“数据集中采集、集中统一分析、疑点分布落实、资源充分共享”的大数据审计模式,使全省的地税联动审计得以实现。

定理1 推导了传统KF和A-KF的状态估计误差方差阵.
定理1.考虑如式(16)和式(17)所示的动态系统,滤波算法如式(13)、(14)、(19)和(20)所示,令

如果低频误差校准参数的估计误差满足如下条件:
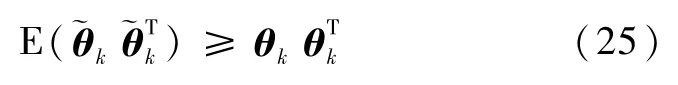
那么状态估计误差满足如下不等式:

限于篇幅,略去定理的证明过程.
定理2给出了定理1中条件(25)成立的充分条件.
定理2.考虑如式(16)和式(17)所示的动态系统,利用如式(19)和式(20)所示的A-KF算法估计低频误差参数θk,如果参数θk满足如下不等式:



定理的证明过程略.由定理2可知,在低频误差参数足够小的情况下,校准误差会大于低频误差参数真值.结合定理1和定理2,得到如下论断:星敏感器低频误差校准对卫星姿态确定精度的影响取决于校准误差和实际低频误差参数的大小对比.如果校准误差大于低频误差参数,那么校准误差将会影响状态估计,导致姿态确定精度下降,此时,不宜进行校准.相反,如果低频误差参数大于校准误差,那么通过校准将消弱低频误差的影响,从而提高卫星姿态确定精度.本文指出了低频误差大小和校准方法使用效果之间的关系,说明同一种误差校准方法应用于不同对象时,可能会得到截然不同的效果,这一结果在以往低频误差校准研究中并未涉及.基于A-KF的低频误差校准方法适合应用于低频误差幅度较大的场合.实际工作中,建议事先对校准误差和低频误差进行对比,其中,校准误差的大小可通过数学仿真确定,低频误差的幅度可基于星上遥测数据进行分析.
3 校准方法性能分析
本节通过计算CRLB(Cramer-Rao lower bound)分析本文所给出的校准方法理论上所能达到的估计精度.CRLB是一种经典的性能评估工具,能够针对特定系统,给出状态估计所能达到的理论下界,或极限精度.CRLB通过系统模型、观测模型,以及相应的噪声方差阵计算得到,其取值反映了系统的本质属性,与具体的滤波方法无关,分析过程中不需要进行滤波解算.
下面简要说明CRLB的计算方法.对于如式(2)和式(6)所示的系统模型,可以得到矩阵Jk,使得

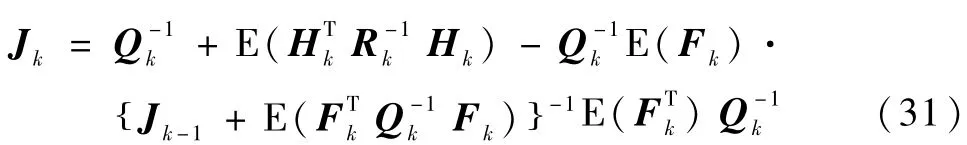
CRLB定义为Fisher信息矩阵的逆.一般来说,较小的CRLB说明所研究的方法是可行的,能够取得较高精度,相反,较大的CRLB说明所研究的方法估计误差较大或不收敛.
计算CRLB的典型仿真条件如下:假定对地指向卫星在周期100min,倾角98°的近圆轨道上运行.星上安装3个陀螺和2个星敏感器,陀螺的角度随机游走和角速率随机游走系数分别为4×10-4(°)/h0.5和5×10-3(°)/h1.5.假定星敏感器光轴指向测量随机噪声标准差为1″.
首先,基于典型仿真条件,通过CRLB分析低频误差校准方法的性能.对应低频误差校准参数ax1、ay1和az1的CRLB的平方根曲线如图1(a)所示.图中,实线表示典型仿真条件下计算得到的估计误差下界.bx1、by1和bz1的曲线与之类似,不再赘述.
不难看出,对于典型仿真条件,本文所给出的低频误差校准方法是有效的.为了分析测量噪声对误差校准的影响,将测量噪声取为典型值的10倍和100倍,并计算CRLB,相应的CRLB平方根曲线如图1(a)所示.在一定的误差水平内,测量噪声对误差校准性能的影响较小.
接下来,分析系统噪声对校准精度的影响.基于不同的系统噪声方差阵,进行3组仿真,系统噪声先取为典型值,再放大10倍和100倍.对于不同的系统噪声水平,对应各个校准参数的CRLB的平方根如图1(b)所示.图形显示,计算得到的CRLB的取值随系统噪声的增大而增大.对于所研究的系统,系统噪声主要由陀螺噪声引起,校准精度与陀螺精度有关.
4 仿真结果
通过仿真分析星敏感器低频误差校准方法的性能.利用通过静态试验得到的三浮陀螺实测数据仿真产生陀螺观测量,低频误差轮廓基于星敏感器遥测数据建立.
低频误差参数通过对2个星敏感器输出的姿态四元数之差进行傅里叶级数拟合得到,表1中给出了仿真中所用的典型低频误差参数.
通过对比误差校准前后的卫星姿态确定精度来说明校准方法的有效性.首先,采用传统姿态确定KF算法处理仿真得到的星敏感器和陀螺观测数据,获得卫星姿态估计值.传统KF的姿态误差曲线如图2(a)所示.
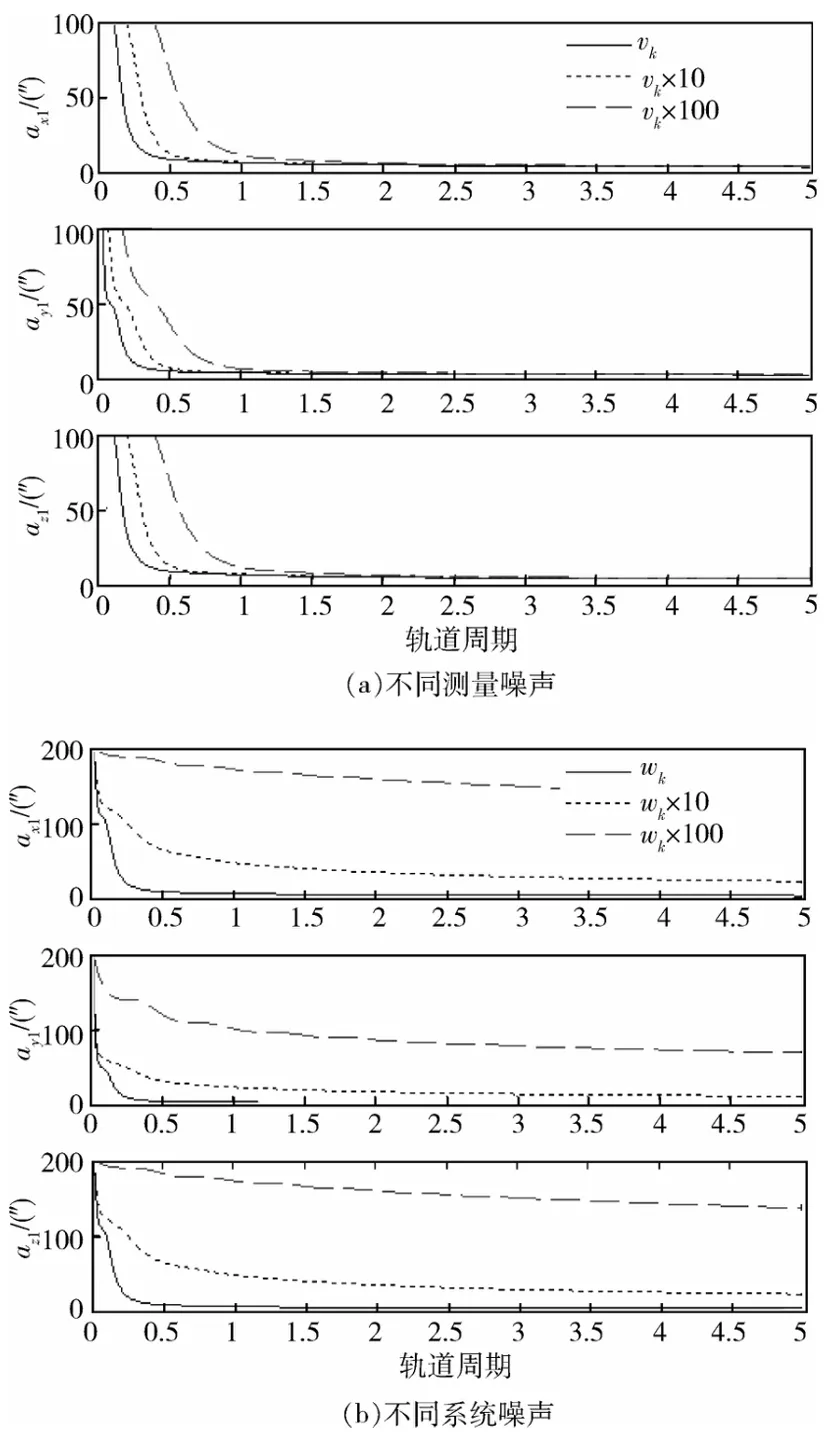
图1 低频误差参数ax1、ay1、az1的CRLB曲线Fig.1 CRLB for low frequency error parameters ax1,ay1 and az1

表1 低频误差参数Tab.1 Low frequency error parameters
其次,利用第3节给出的低频误差校准方法,得到的姿态估计误差曲线如图2(b)所示.与传统KF的估计结果进行对比,可以看出,KF不能有效消除星敏感器低频误差的影响,应用低频误差校准方法后,姿态确定误差显著减小.
接下来,分析低频误差的幅度较小时,误差校准对姿态确定精度的影响.将低频误差参数设置为表1中所示数据的1%时,通过传统KF和A-KF得到的卫星姿态估计误差曲线如图3所示.
正如本文所分析的,在低频误差较小的情况下,通过A-KF校准后,相对于不进行校准的情况,姿态确定精度有所降低.此时,不宜进行误差校准.
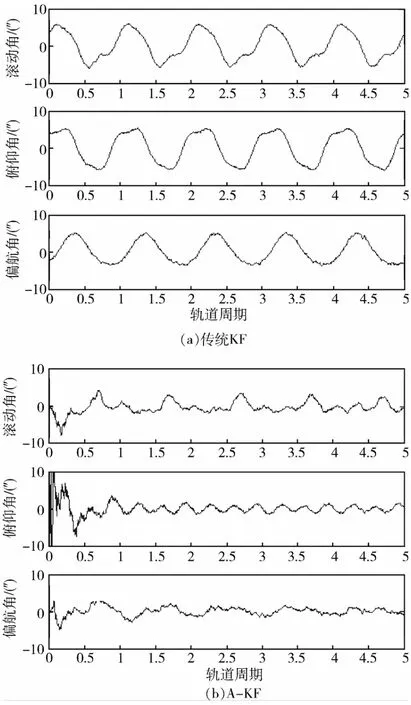
图2 低频误差取典型值情况下的卫星姿态确定误差曲线Fig.2 Satellite attitude determination error with typical low frequency error
对于不同的低频误差参数取值,通过传统KF和A-KF得到的卫星姿态估计误差均方根(RMS)如表2所示,表中最后一列为均方根误差的范数.
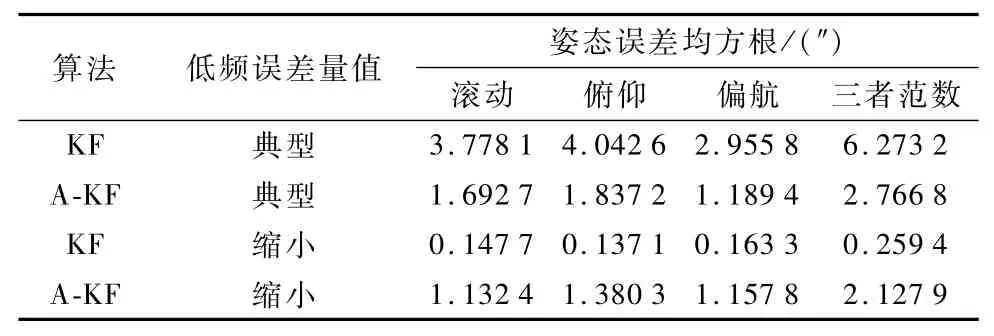
表2 校准前后姿态估计误差对比Tab.2 Comparison between attitude estimation errors before calibration and after calibration
不难看出,低频误差幅度较大的情况下,A-KF的估计精度优于传统KF;低频误差幅度较小的情况下,传统KF的估计精度优于A-KF.
为了更清楚的说明低频误差校准方法的有效性与低频误差幅度大小的关系,设置低频误差参数为多个不同值,测试传统KF和A-KF的性能.低频误差参数分别设置为表1中数值的10%、20%、30%、50%、100%、200%和300%,仿真得到的三轴姿态估计误差均方根的范数如图4所示.

图3 低频误差缩小情况下的卫星姿态确定误差曲线Fig.3 Satellite attitude determination error with decreased low frequency error

图4 姿态确定精度和低频误差的关系Fig.4 Relation between attitude determination accuracy and low frequency error
显然,随着低频误差的增大,传统KF的估计精度显著降低,而A-KF估计精度降低的程度相对较小,逐渐体现出相对传统KF的优势.对于典型低频误差参数量级和现有陀螺精度水平,通过校准有利于提高卫星定姿精度.
5 结 论
针对星敏感器低频误差影响卫星姿态确定精度的问题,提出了将星敏感器低频误差建模为傅里叶级数,并通过A-KF估计低频误差参数的方法,通过理论推导和数学仿真详细分析了低频误差校准方法的性能.为了保证仿真的可信度,采用根据星敏感器遥测数据建立的低频误差模型,并将实测陀螺数据用于数学仿真.研究表明,当校准误差小于低频误差参数真值时,通过低频误差校准能够提高卫星姿态确定精度,相关分析结果能够为低频误差校准方法的设计和选用提供参考.
[1]CRASSIDIS J L, MARKLEY F L, CHENG Y.Survey of nonlinear attitude estimation methods[J].Journal of Guidance, Control, and Dynamics, 2007, 30(1):12-28.
[2]JORGENSEN J L,DENVER T,BETTO M,et al.The PROBA satellite star tracker performance[J].Acta Astronautica, 2005, 56:153-159.
[3]JORGENSEN P S, JORGENSEN J L, DENVER T, et al.In-flight quality and accuracy of attitude measurements from the CHAMP advanced stellar compass[J].Acta Astronautica, 2005, 56:181-186.
[4]IWATA T,HOSHINO H,YOSHIZAWA T,et al.Precision attitude determination for the advanced land observing satellite(ALOS):design, verification, and onorbit calibration[C].AIAA-2007-6871,2007.
[5]WINKLER S,WIEDERMANN G,GOCKEL W.Highaccuracy on-board attitude estimation for the GMES Sentinel-2 satellite:concept, design, and first results[C].AIAA-2008-7482,2008
[6]XIONG K,TANG L,LEI Y J.Multiple model Kalman filter for attitude determination of precision pointing spacecraft[J].Acta Astronautica, 2011, 68:843-852.
[7]ZHANG X,WILLETT P,BAR-SHALOM Y.Dynamic Cramer-Rao bound for target tracking in clutter[J].IEEE Transactions on Aerospace and Electronic Systems, 2005, 41:1154-1167.
