基于线性协方差的月球上升器主动段误差分析

王志文，张洪华

(北京控制工程研究所，北京100190)

0 引 言

月球上升段由3个阶段构成，如图1所示.第一阶段是100m的垂直上升，该阶段所用时间很短，主要目的是使探测器离开月面，达到动力上升所需要的条件.第二阶段是单轴旋转，该阶段要求在尽量短的时间里调整上升器的姿态，使推力方向的指向从垂直方向转为动力上升段开始时所要求的最优指向.第一和第二阶段，一般采用开环制导律.第三阶段是动力上升段，即主动段.以美国Altair月球着陆器为例，该阶段要求上升器到达近月点约15km、远月点约75km的椭圆轨道.该阶段飞行时间较长，一般有300多秒，故需要设计闭环最优控制使得该段所消耗的燃料最少[1-3].

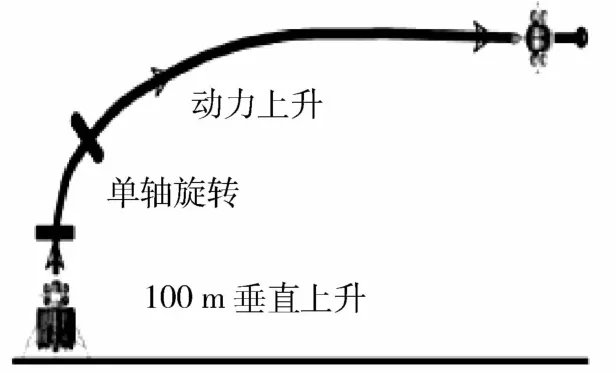
图1 月球上升器3个阶段[1]Fig.1 Three stages for lunar ascent

本文使用线性协方差的方法研究第三阶段制导，即主动段制导，在存在初始状态偏差和系统参数偏差的情况下，终端高度、速度大小以及飞行路径角的偏差.其中，主动段制导采用的制导律为PEG+保持制导[4].在用线性协方差分析PEG制导性能之前，首先需要对PEG进行线性化.文献[4]使用了一种数值方法实现了对PEG的线性化处理，但这种方法运算量大，需要时间较长，且面临着步长选择的问题.本文提出一种解析的方法，可以得到PEG3 个制导参数的线性化显式表达，相比而言可以大幅减少运算量和仿真时间.通过对PEG线性化处理，可以考察主动段制导存在初始状态偏差(位置偏差和速度偏差)、系统参数偏差(比冲偏差、质量偏差和质量流量偏差等)以及执行机构偏差的情况下，终端时刻的制导偏差.

1 制导律简介

如引言所述，本文采用PEG+保持制导.PEG是一种预测校正的迭代制导律.

考虑运动方程

式中，F为推力，m为当前质量，g为当前位置月球重力加速度，uf为推力方向单位矢量，且具有如下形式:

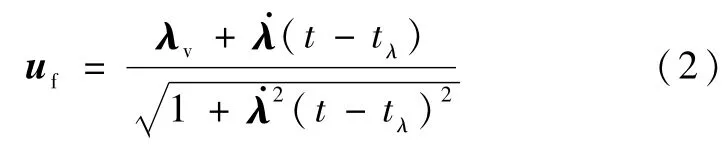
式中，λv为速度增量方向上单位矢量垂直于表示推力方向的变化.tλ为制导时间，选择合适的数值，可使得推力引起的速度变化沿着λv方向.uf，三者之间的关系如图2所示.PEG制导的主要问题是得到这3个制导参数，然后按照式(2)就可以计算任意时刻推力方向的单位矢量.

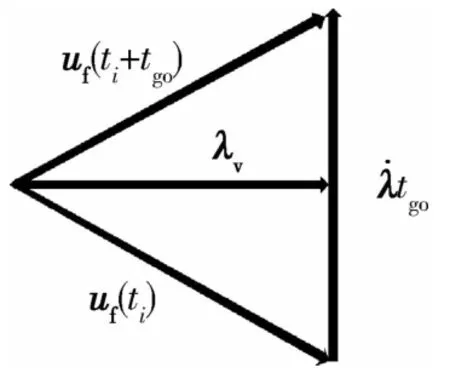
图2 制导参数之间的关系Fig.2 Relations of guidance parameters

关于PEG制导的详细推导过程这里不再赘述，读者可以参考相关文献[4-6].需要说明的是，PEG以速度增量vgo作为其独立变量，使用预测校正的迭代方法产生满足终端要求的vgo，在此基础上得到PEG制导律3个制导参数λv，，tλ的显式表达.

2 线性协方差分析

线性协方差分析作为一种误差分析方法已经被成功应用于交会对接、地月轨迹、行星任务的GNC系统和导航分析.和蒙特卡洛方法相比，线性协方差方法速度快，一次运行就可以得到误差的分析结果，并且可以随意选择误差组合，分析不同误差带来的影响.

将线性协方差用于主动段制导误差分析，首先面临的一个困难是将PEG制导律线性化.如前所述，PEG制导律复杂，高度非线性，并且包含预测校正的迭代求解过程，所以将其线性化比较困难.本文给出一种近似的PEG线性化解析方法，得到了PEG3 个制导参数的线性化显式表达.

制导在tgo=tf时转入保持模式，从蒙特卡洛仿真的角度来看，不同样本从PEG转入保持模式的时间都是不一样的，所以针对这种基于事件触发而不是时间触发的制导模式转换，线性协方差分析需要进行相应的修正，这也就是文献[4]中提到的事件触发的问题.

最后，当制导转入保持模式后，推力单位矢量保持不变，但这个时候推力单位矢量的偏导并不为零，也并不等于从PEG转入保持模式时刻的偏导值，即线性协方差分析还需要解决保持模式中推力方向偏导问题[4].

下面将根据这3个问题依次进行说明.

2.1 系统状态定义

影响月球上升段主动段制导精度的有:初始位置偏差δr，初始速度偏差δv，比冲偏差δIsp，初始质量偏差δm，初始质量流量偏差δdm，推力大小偏差δF，以及执行机构偏差.其中执行机构参数偏差包括零偏误差b，标度因数误差f，失准误差κ.此外对制导精度有影响的还有重力模型偏差εgrav，以及环境噪声等.

设系统状态为

2.2 PEG线性化

PEG制导律线性化中所有的偏差都是相对于标称轨迹来说的.标称轨迹是由理想初始条件并忽略所有中间过程误差生成的.规定下面符号均表示x的标称值.

PEG制导律线性化指的是线性化PEG制导律的3个制导参数由PEG的制导方程可知

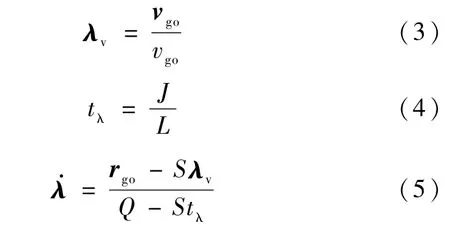
线性化式(3)和(4)有

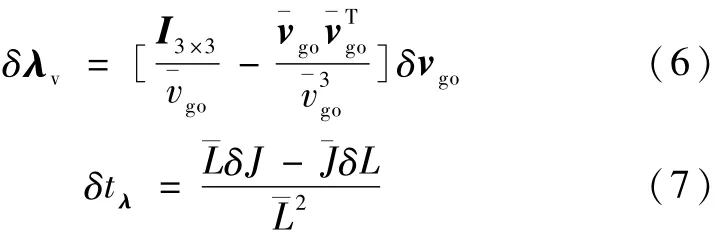
由上述J，L的定义可知，其偏差δJ，δL可以写成关于的线性表达，如下所示:

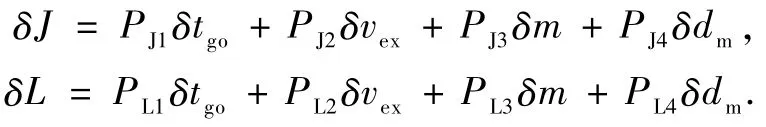
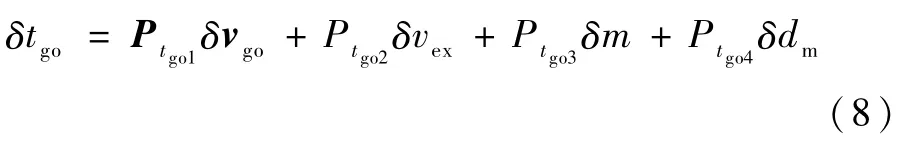
综上可以看出要得到δλv，δtλ，只需要得到δvgo就可以了.

线性化式(5)有

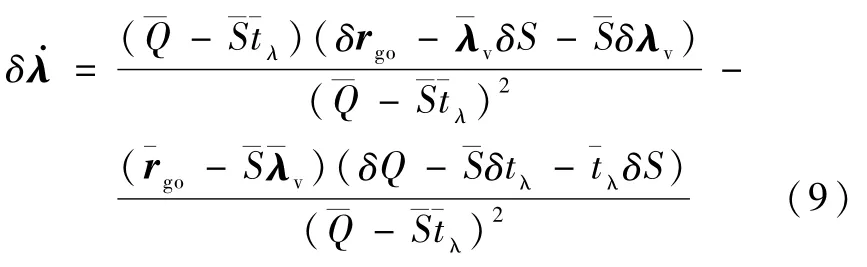
同理δS，δQ可写为如下的线性表达:

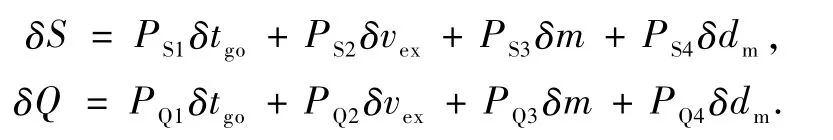
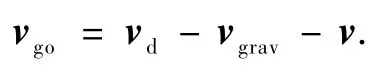
式中，vd为期望的终端速度，为当前的速度.

线性化有

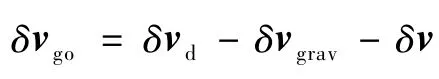
经过推导，δvgo可以写为关于的线性表达

近似认为

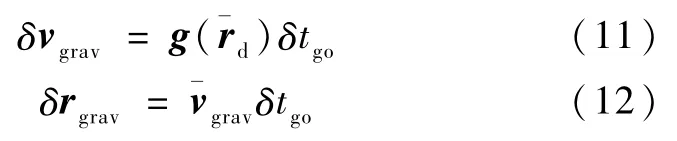
结合式(8)、(11)、(12)可知，δvgo可以进一步写为如下的线性表达:

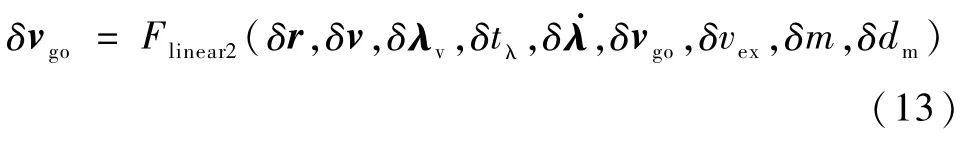
至此，可以得到δvgo的最简线性化表达

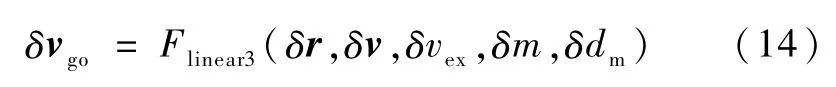
对于rgo的线性化δrgo，思路和上面类似.需要注意的是在PEG制导方程中，rgo的计算分两步:第一步按着计算，然后利用约束修正rgo.所以在线性化rgo的时候也应该按着这样的两步线性化.最终，δrgo也可以写为如下的最简线性化表达:

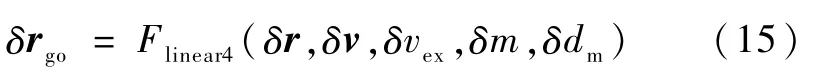
得到了vgo，rgo的线性化表达，代入就可以得到PEG3个制导参数的线性化表达

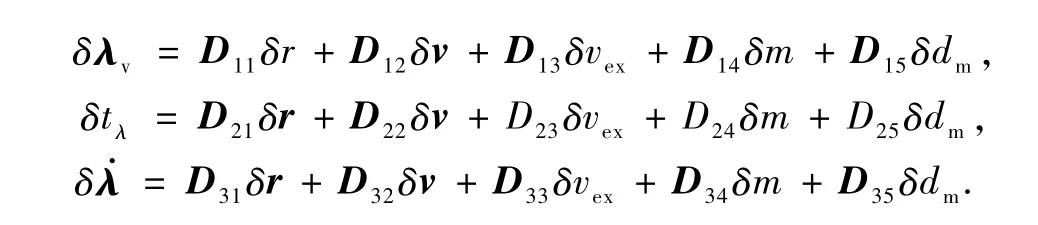
2.3 事件触发

如前所述，设定PEG转出的时间阀值tf，当tgo=tf时制导转入保持模式.由于这种模式转换不是基于固定的时间，而是基于离散的事件(tgo=tf)，所以线性协方差需要进行相应的修正[4].

关于包含事件触发的线性协方差分析，文献[7]中给出了较为详细的推导.本文将其原理应用于主动段模式转换时线性协方差分析.对一般情况，事件触发可以用数学表达式表示成如下关于状态的函数[7]:

式中，x表示系统状态，当等式满足时意味着该事件在te时刻发生了.在本文中，该事件可以具体表示为

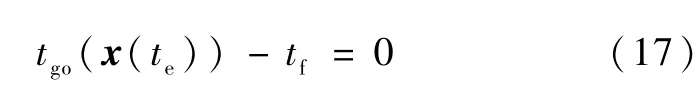
这里省略具体的推导过程，只给出最后的结论[7]

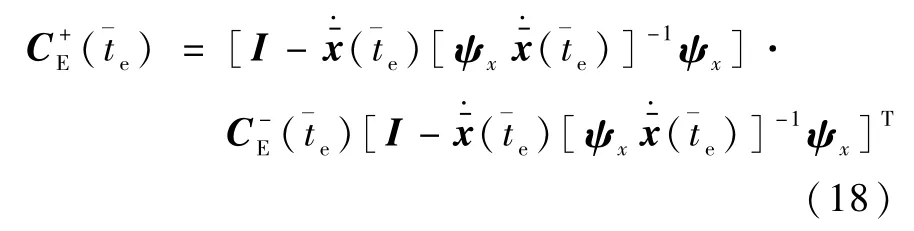
2.4 保持模式中单位推力的偏导

当tgo=tf时制导转入保持模式，在这个阶段，系统将保持PEG制导最后一步的推力方向不变，直到tf时间后主发动机关机，制导结束.

虽然在保持模式中推力方向保持不变，但推力方向的偏导并不是零.这是因为，从蒙特卡洛仿真的角度分析，不同的样本在进入保持模式时推力方向不同，而线性协方差中推力方向的偏导统计的就是不同样本相对于标称轨迹的偏差.而且保持模式中推力方向的偏导也不等于PEG最后时刻(进入保持模式之前)的偏导，否则就意味着保持模式中推力方向的偏差是由该阶段系统状态的变化所导致的[4].

文献[4]给出了一种解决方法，即引入一个虚拟状态uf，uf表示推力单位矢量.这时系统的状态重写为

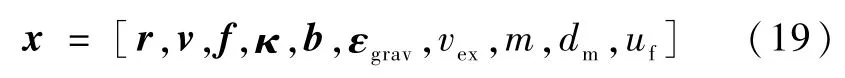
uf由PEG制导得到，每调用一次PEG，就更新一次uf，所以可以认为uf的动力学为[4]

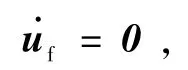
uf的更新方程如下[4]:

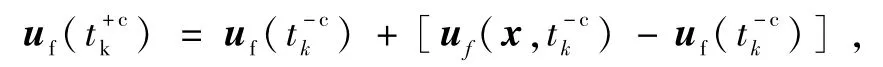
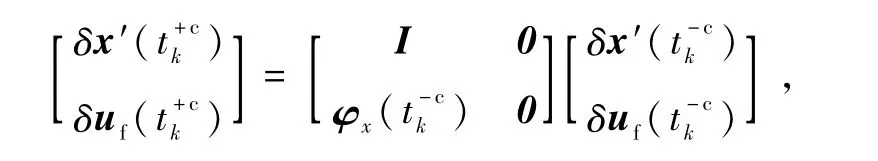
于是可以得到更新后系统协方差矩阵

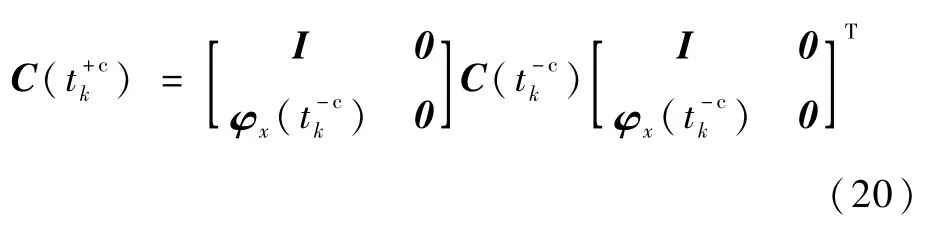
式(20)表示每调用一次PEG，系统协方差矩阵就更新一次，直到保持阶段，不再调用PEG.

2.5 系统误差源建模

本文将执行机构偏差中包含的f，κ，b以及重力模型偏差εgrav均视为一阶马尔科夫过程[8].

对每个执行机构参数pj，其状态协方差为时间常数为τj，白噪声方差如下:

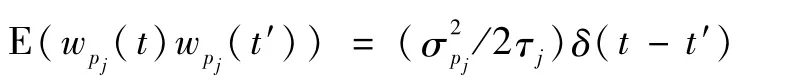
其动力学方程可写为

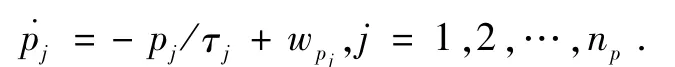
对重力模型偏差εgrav，其状态协方差为相关距离为dk，白噪声方差如下:

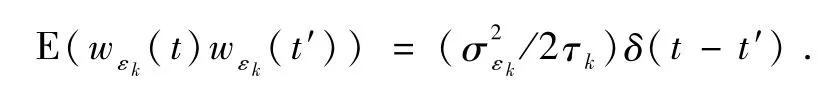
其动力学方程可写成如下的分量形式:

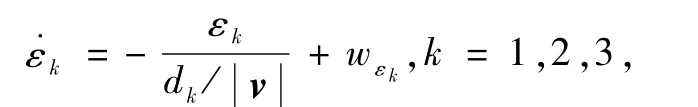
系统参数认为保持不变，故

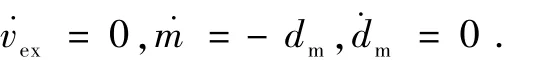
3 仿真及分析

上升器主动段终端关注高度，速度大小，以及飞行路径角的大小.本文按着PEG+保持的制导模式(tf=8s)，用上述线性协方差方法分析在存在初始状态偏差、系统参数偏差以及执行机构偏差的情况下，终端高度、速度大小、飞行路径角的偏差.为了验证上述线性协方差的有效性，引入了相同初始条件下的300次蒙特卡洛仿真.仿真中用到的执行机构参数偏差和噪声如表1[9]所示.

表1 仿真参数Tab.1 Simulation parameters

按着初始仿真条件，分为如下两种情况:

其中情况2相对于情况1，增加了参数vex，m，dm的偏差，以考察系统参数偏差对PEG制导性能的影响.

图3和图4给出了两种不同初始条件下线性协方差(LC)和蒙特卡洛(MC)关于高度偏差δh，速度大小偏差δv，以及飞行路径角偏差δγ的对比曲线.从图中可以看出，在305s之前有一个突变，这是由蒙特卡洛在处理从PEG转入保持模式的数据时重置不同样本的仿真时间为一个共同的仿真时间e(e为标称情况下从PEG转入保持模式的时间)所造成的.这样处理的结果方便MC与LC进行直接比较分析.同时从图中还可以看出，经过8s的保持模式，在制导结束时刻，LC和MC的结果重合较好，且都趋向于零.说明在存在上述偏差的情况下，PEG+保持模式的制导模式能够保证终端精度要求.

从图中可以看出，LC和MC的仿真曲线在过程中间时刻有一些偏差，这主要是由于本文提出的线性协方差分析是一种近似的分析，本身PEG线性化存在误差，但实际中更关注的是终端时刻的状态偏差，从图中两种情况的仿真分析可以看出，终端时刻LC和MC两条仿真曲线基本重合，表明上述的线性协方差方法可以较好地估计终端时刻的状态偏差.

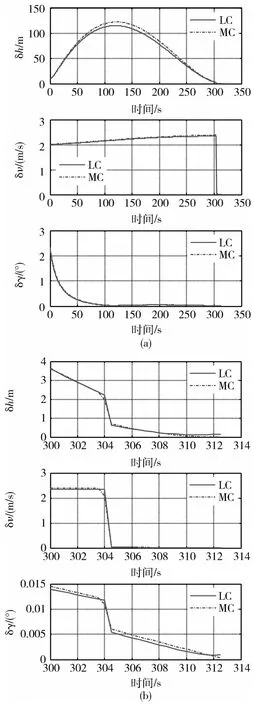
图3 情况1仿真图Fig.3 Simulation results in Condition one

在存在初始状态偏差，系统参数偏差以及执行机构偏差的情况下，制导终端状态偏差都趋于零，可以看出PEG具有较好的鲁棒性.然而这种分析其实暗含了一个前提，就是系统的这些初始参数偏差，状态偏差都必须是已知的，也就是“可观的”.换句话说，制导计算机中存储的初始状态以及系统参数必须和实际上升器初始时刻的状态和参数一致.在实际应用中，上述两部分对应的参数通常不能保证一致，所以需要在线估计实际上升器的参数，并把辨识得到的参数传给制导计算机来产生制导指令，这样就可以保证制导计算机中的上升器参数和实际上升器的参数保持一致.

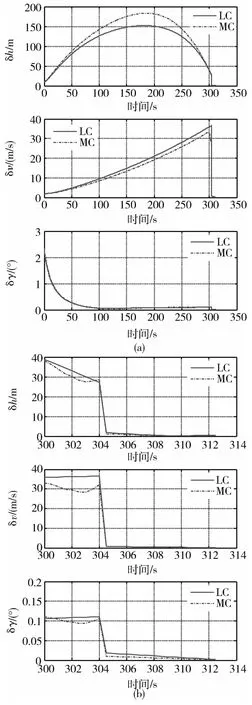
图4 情况2仿真图Fig.4 Simulation results in condition 2

4 结 论

本文提出了一种解析的PEG线性化方法，应用于月球上升器主动段误差分析.研究了主动段在存在初始状态偏差和系统参数偏差以及执行机构偏差的情况下，终端时刻的高度偏差、速度大小偏差、以及飞行路径角偏差.最后通过和蒙特卡洛的仿真对比，验证了本文提出的PEG线性化方法的有效性，可以看出在系统参数“可观”的情况下，PEG具有较好的鲁棒性.同时需要说明的是，本文提出的PEG线性化分析没有考虑导航误差以及姿态控制方面的影响，这也是后续研究中需要着重考虑的问题.

[1]KOS L D，POLSGROVE T T，SOSTARIC R R，et al.Altair descent and ascent reference trajectory design and initial dispersion analyes[R].20100035768，2010.

[2]SOSTARIC R R，MERRIAM R S.Lunar ascent and rendezvous trajectory design[R].20080009584，2008.

[3]BENNETT F V.Apollo experience reportmission planning for lunar module descent and ascent[R].19720018205，1972.

[4]ROSE M B，GELLER D.Linear covariance techniques for powered ascent[R].AIAA20108175，2010.

[5]MCHENRY R L， BRAND T J， LONG A D， et al， Space shuttle ascent guidance， navigation， and control[J].Journal of Astronautical Sciences， 1979，28(1):1-38.

[6]SPRINGMANN P，PROULX R，FILL T.Lunar descent using sequential engine shutdown[R].2006-6678，2006.

[7]GELLER D K，ROSE M B，WOFFINDEN D C.Event trigger in linear covariance analysis with application to orbital rendezvous[J].Journal of Guidance， Control，and Dynamics， 2009，32(1):102-111.

[8]GELLER D K，CHRISTENSEN D P.Linear covariance analysis for powered lunar descent and landing[J].Journal of Spacecraft and Rockets，2009，46(6):1231-1235.

[9]MOESSER T J.Guidance and navigation linear covariance analysis for lunar powered descent[D].Logan Utah State:Utah State University，2010.