水滴撞击特性的高效计算方法

周志宏，易 贤，桂业伟，李凤蔚

（1．中国空气动力研究与发展中心 空气动力学国家重点实验室，四川 绵阳 621000；2．西北工业大学航空学院，陕西 西安 710072）

水滴撞击特性的高效计算方法

周志宏1，易 贤1，桂业伟1，李凤蔚2

（1．中国空气动力研究与发展中心 空气动力学国家重点实验室，四川 绵阳 621000；2．西北工业大学航空学院，陕西 西安 710072）

针对拉格朗日方法计算水滴撞击特性效率低、通用性差等问题，发展了一种水滴撞击特性的高效计算方法。在求解绕流流场的基础上，结合逐级结构化管理的边界信息存储方式，采用目标扩散追踪方法对水滴所在网格单元进行快速计算，并插值得到该点处的流场信息，逐个求解水滴运动方程得到各水滴的运动轨迹，从而确定水滴撞击极限、收集系数等撞击特性参数。通过对NACA0012翼型、GA-W（1）两段翼型和某三段翼型的计算得到不同状态下的水滴撞击特性，计算结果表明，该方法与传统方法相比具有计算效率高、结果可靠、通用性好等优点。

结冰；水滴撞击特性；目标扩散追踪方法；拉格朗日法

0 引 言

结冰会改变飞机的绕流流场，破坏空气动力学性能，影响飞机的操纵性和稳定性，危害飞行安全，严重时能导致机毁人亡的严重事故［1］。我国幅员辽阔，气象条件非常复杂，飞机结冰现象比较常见，随着民用航空运输业的发展、飞机飞行密度的提高以及对飞机全天候飞行的要求，飞行中遭遇到结冰气象条件的几率更是大幅提高，结冰已成为飞行安全事故的主要隐患之一［2］。

水滴撞击特性研究是飞机结冰研究的主要内容之一，是结冰预测以及防／除冰系统设计的基础［3］，水滴撞击特性的计算方法主要有拉格朗日和欧拉两种方法［4］。拉格朗日法是在模拟绕流流场的基础上，采用差分法逐个求解水滴运动方程，得到各水滴的运动轨迹，进而求得水滴撞击区域和形体表面上的局部水收集系数等参数［5］，确定水滴的撞击特性。该方法形式简单，方法成熟，尤其是模拟SLD（过冷大水滴）成冰过程时［6-7］，它能比欧拉方法更直观、方便的体现大水滴在运动、撞击过程中的变形、破碎、飞溅等动力学行为的局部运动细节，因此被广泛应用于积冰研究中。

拉格朗日方法求解水滴运动方程时，每个时间步都必须计算水滴所属网格单元，现在的处理方法通常是采用全场网格遍历的方法搜索水滴所处网格单元［8］，这种方法计算量大，水滴是否撞击到物面的判断过程繁杂，对于三维外形和不连通的多段结冰面（如多段翼型）的撞击判断尤其难度大、方法通用性差［9-10］。由于对每个水滴在各个时间步上都进行一次全场网格遍历效率太低，本文提出的目标扩散追踪方法将水滴当成追踪目标，沿着水滴飞行的轨迹进行扩散追踪，采用射线求交法判断水滴与网格单元的内外关系，大大提高了计算效率；并通过简洁、高效的结构化边界信息管理方式，成功解决了传统方法计算不连通的多段结冰面通用性差、判断水滴是否与物面相撞困难等问题。本文方法为飞机防除冰系统的设计中飞机部件水滴撞击特性提供了一种快速、准确的计算方法。

1 计算方法

水滴撞击特性的拉格朗日计算过程分两步：首先，用CFD方法求解绕流空气流场；然后，在流场解的基础上求解水滴轨迹，进而获得水滴撞击极限、水滴收集率等水滴撞击特性参数。

1.1 空气流场计算

空气流场积分形式控制方程为［11］：

采用Van Leer迎风格式进行离散，应用LUSGS隐式格式进行时间推进，结合SA一方程湍流模型获得绕流流场定常解［12］。

1.2 水滴撞击特性计算

1.2.1 水滴轨迹运动方程的求解

建立水滴运动方程时，作如下假设：①水滴体积很小，不会影响流场的性质；②水滴在运动过程中不碰撞、不合并、不分裂，水滴尺寸保持不变；③水滴在运动过程中和周围空气不发生质量、热交换，温度、粘性、密度等介质参数保持不变［13-14］。

考虑作用在水滴上的重力、浮力和阻力，根据牛顿第二定律，水滴轨迹运动方程可以写成［15］：

每个水滴轨迹运动方程均可当成一阶常微分方程的初值问题来求解，从远处开始计算水滴的运动轨迹，采用四步龙格-库塔方法，由i时刻的水滴及其绕流信息得到i＋Δi时刻的水滴位置、速度，水滴绕流信息由所处网格单元各节点信息插值得到，当水滴流出边界或撞击到部件时开始计算下一水滴轨迹，直到完成所有水滴的轨迹计算。

1.2.2 水滴所处单元的搜索

水滴轨迹计算过程中，每个时间步上都要进行水滴网格单元的搜索，搜索方法的快慢直接影响到结冰模拟算法的效率。特别在过冷大水滴结冰时，为精确捕捉大水滴在运动、撞击过程中的动力学细节，需计算的水滴数量运比常规小水滴结冰模拟时要多，提高水滴所处单元的计算效率尤为重要。

传统全场遍历方法的效率太低，本文提出一种目标扩散追踪方法来计算水滴所在网格单元，采用射线求交法判断水滴与网格单元的内外关系，以前一时间步水滴坐标为起点，以本时间步水滴坐标为目标位置进行扩散追踪以计算水滴所处的网格单元。计算发现，由于步长很小，水滴在一个时间步的移动距离基本都在一至两个网格单元之间，除了在物面附近极密的粘性网格外，其他绝大部分位置只需要进行一、两次简单的位置判定就能获得水滴所属网格单元。该方法将传统方法中的全流场的遍历过程简化为几次简单的线段相交计算，大大节省了计算时间，极大地提高了搜索效率。

以二维情况下对一个水滴进行扩展目标搜索为例，其过程如下：

1）水滴初始位置坐标为（xA，yA），全场搜索该点所处网格单元（I0，J0）。

2）由网格单元（I0，J0）各节点处的值插值得到水滴绕流信息，求解水滴轨迹方程，得到Δi时间后水滴位置坐标（xB，yB）。

3）计算AB与网格单元（I0，J0）四条边的交点。若全不相交，则B点仍处于网格单元（I0，J0）中，水滴新位置A的坐标值为：xA＝xB，yA＝yB，返回2）；若与某条边相交，该边不属于块边界则进行第4步，该边属于块边界则进行第5步。

4）水滴流入与该边相邻的网格单元中，从相交点往B方向延伸一个很小的量，该点坐标为（xC，yC），水滴新位置A的坐标值为：xA＝xC，yA＝yC，返回3）。

5）判断该边的边界条件：若为对接边界，则新的网格单元为相邻网格块上对应的单元，其序号采用计算空气流场对接边界条件时的方式得到，从相交点往B方向延伸一个很小的量，该点坐标为（xC，yC），水滴新位置A的坐标值为：xA＝xC，yA＝yC，返回3）；若为远场边界，则水滴流出计算域，结束该点追踪；若为物面边界，此时水滴撞击到形体上，记录撞击位置，结束该点追踪。

1.2.3 水滴撞击物面的判定

水滴撞击点的传统计算方法需要在每个时间步判定水滴与形体的相对关系，并计算水滴轨迹线与所有物面网格线是否有交点，过程十分繁琐、计算量庞大，且很难用一个通用程序来处理不同复杂几何构型。采用目标扩散追踪方法计算水滴所处网格单元时，在上述方法第5步的计算过程中就直接得到了水滴与物面的撞击点，不需进行额外的特殊处理，而这需要依赖于本文所采用的由上而下逐级结构化管理的边界信息储存方式。

将网格块中各面的边界信息以“区”为单位存储，按照“块”、“面”、“区”顺序对各网格块的边界信息进行结构化管理，每个存储单位中的信息包含该“区”所属网格块、所处边界面、该“区”序号、边界类型、网格点起始点与结束点等信息，将搭接边界分为左右两部分，按照相应的块、起始结束点序号以及搭接方向一一对应。这种逐级结构化的边界信息管理方式能保证程序不受计算网格拓扑结构的限制、可灵活应用于不同复杂几何外形。

通过结构化的边界信息储存方式，水滴轨迹计算过程中可快速得到与水滴轨迹线相交的网格单元边的信息，实现高效、准确的水滴碰撞计算。

1.3 水滴撞击特性的确定

确定水滴运动轨迹之后，可进一步得到防冰部件的水滴撞击极限、总收集系数、局部水收集系数等水滴撞击特性参数［16］，用于防冰系统的设计。

2 算例与分析

通过不同外形水滴轨迹的数值模拟及其与相关实验数据的对比对方法进行了检验和验证。

2.1 方法效率测试

对规模为7880、14820、23760的NACA0012翼型网格，规模为17600的GA-W（1）两段翼型网格（网格分为三块），规模为14720的某三段翼型网格（网格分为四块）分别采用直接搜索方法和本文方法进行300个水滴点的跟踪计算，直接搜索方法耗时分别为14．4s、26．1s、44．7s、41．3s、35．4s，本文方法耗时分别为1．3s、1．5s、1．7s、1．4s、1．3s。计算结果表明扩展目标追踪方法能大幅提高计算效率，且计算效率受网格规模、拓扑结构的影响不大，网格越密、拓扑结构越复杂，其优势就越明显。

2.2 方法准确性测试

图1 NACA0012翼型撞击极限及水滴轨迹Fig.1 Trajectories and impingement limit of water droplets for NACA0012 airfoil

对长度为0．5334的NACA0012翼型进行了水滴轨迹计算，气象条件如下：M＝0.32，p＝89867Pa，LWC＝0．55g／m3。case1中MVD＝15μm；case2中MVD＝40μm。图1为采用本文方法计算得到的case1、case2下的水滴轨迹以及撞击极限，图2为计算局部收集系数（Beta）与实验值的对比，s为翼型上的水滴撞击点到驻点的距离，上表面为正，下表面为负，s＝0处为局部收集系数达到最大值的位置。计算结果与参考文献［17］中给出的目前公认结冰计算能力最强的软件Lewice的结果基本上一致，表明本方法的计算结果是准确可靠的。

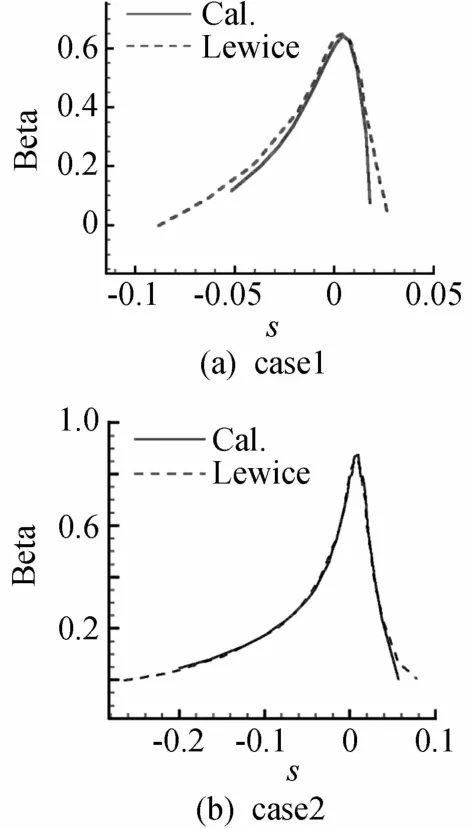
图2 水滴收集系数与试验结果的对比Fig.2 Water collection coefficient compared with the experiment data

2.3 方法通用性测试

在M＝0．27，α＝2．0°，Re＝0．1E＋7，MVD＝20．0μm，p＝1．013×105Pa，T＝262．9K条件下，分别对带30%子翼的GA-W（1）两段翼型和某三段翼型进行水滴轨迹计算，水滴运动轨迹及撞击区域如图3、图4所示；各段的水滴收集系数分布规律如图5、图6所示，计算结果合理，这表明本方法可对各种不连通几何外形进行水滴撞击特性的计算。

图3 GA-W（1）两段翼型水滴轨迹及撞击极限Fig.3 Trajectories and impingement limit of water droplets for GA-W（1）two-element airfoil

图4 某三段翼型水滴轨迹及撞击极限Fig.4 Trajectories and impingement limit of water droplets for three-element airfoil

图5 GA-W（1）两段翼型水滴收集系数Fig.5 Water collection coefficient for GA-W（1）two-element airfoil

图6 某三段翼型水滴收集系数Fig.6 Water collection coefficient for three-element airfoil

3 结 论

本文提出的水滴撞击特性的拉格朗日计算方法基于目标扩散追踪方法以及边界信息结构化管理，克服了常用方法计算大量水滴的撞击特性时计算量大、水滴撞击判断过程繁杂、应用于复杂外形的通用性差等缺点，具有计算效率高、计算结果可靠、对复杂外形通用性好等优点，为飞机防除冰系统的设计中飞机部件水滴撞击特性提供了一种快速、准确的计算方法。

［1］ISAAC G A，et al．Recent Canadian research on aircraft inflight icing［J］．Canadian Aeronautics and Space Journal，2001，47（3）：213-222．

［2］HONSEK R，HABASHI W G，AUBE M S．Eulrian modeling of in-flight icing due to supercooled large droplets［J］．Journal of Aircraft，2008，45（4）：1290-1296．

［3］SUN Z G，ZHU C X，ZHU C L．Development of s of tware for aircraft icing simulation［J］．Computer Simulation，2012，29（4）：104-107．（in Chinese）

孙志国，朱程香，朱春玲．飞机结冰数值仿真软件开发［J］．计算机仿真，2012，29（4）：104-107．

［4］ZHANG D L，YANG X，ANG H S．Numerical simulation of supercooled water droplets impingement on icing surfaces［J］．Journal of Aerospace Power，2003，18（1）：197-201．（in Chinese）

张大林，杨曦，昂海松．过冷水滴撞击结冰表面的数值模拟［J］．航空动力学报，2003，18（1）：197-201．

［5］COSSALI G E，COGHE A，MARENGO M．The impact of a single drop on a wetted solid surface［J］．Experiments in Fluids，1997，22（6）：463-472．

［6］ZHANG C，KONG W L，LIU H．An investigation on the breakup model for icing simulation of supercooled large droplets［J］．ACTA Aerodynamica Sinica，2013，31（2）：144-150．（in Chinese）

张辰，孔维梁，刘洪．大粒径过冷水滴结冰模拟破碎模型研究［J］．空气动力学学报，2013，31（2）：144-150．

［7］BOURGAULT Y，HABASHI W G，DOMPIERRE J，et al．An Eulerian approach to supercooled droplets impingement calculations［R］．AIAA-97-0176，

［8］YANG Q，CHANG S N，YUAN X G．Study on numerical method for determining the droplet trajectories［J］．ACTA Aeronautica et Astronautica Sinica，2002，23（2）：173-176．（in Chinese）

杨倩，常士楠，袁修干．水滴撞击特性的数值计算方法研究［J］．航空学报，2002，23（2）：173-176．

［9］YI X，WANG K C，GUI Y W．Study on Eulerian method for icing collection efficiency computation and its application［J］．ACTA Aerodynamica Sinica，2010，28（5）：596-602．（in Chinese）

易贤，王开春，桂业伟．结冰面水滴收集率欧拉计算方法研究及应用［J］．空气动力学学报，2010，28（5）：596-602．

［10］TRUJILLO M F，MATHEWS W S，LEE C F，et al．Modeling and experiments of impingement and atomization of a liquid spray on a wall［J］．International Journal of Engine Research，2000，1（1）：87-105．

［11］SHIN J，BERKOWITZ B，GHEN H H，et al．Prediction of ice shapes and their effect on airfoil drag［J］．Journal of Aircraft，1994，31（2）：301-316．

［12］ZHOU Z H．Navier-Stokes analysis in complex configurations and icing simulation on airplanes［D］．Xi′an：Northwestern Polytechnical University，2011．

［13］CHANG S N，YANG Q M，LI Y．Quasi-steady numerical simulation of ice accretion on airfoil［J］．ACTA Aerodynamica Sinica，2011，06：302-308．（in Chinese）

常士楠，杨秋明，李延．翼型表面结冰准定常数值模拟［J］．空气动力学学报，2011，06：302-308．

［14］PAPADAKIS M，RACHMAN A，WONG S C，et al．Waterimpingement experiments on a NACA 23012 airfoil with simulated glaze ice shapes［R］．AIAA 2004-0565，2004．

［15］YI X，ZHU G L，WANG K C，et al．Numerically simulating of ice accretion on airfoil［J］．ACTA Aerodynamica Sinica，2002，20（4）：428-433．（in Chinese）

易贤，朱国林，王开春，等．翼型积冰的数值模拟［J］．空气动力学学报，2002，20（4）：428-433．

［16］YI X，ZHU G L．Computation of glaze ice accretion on airfoil［J］．ACTA Aerodynamica Sinica，2004，22（4）：490-493．（in Chinese）

易贤，朱国林．考虑传质传热效应的翼型积冰计算［J］．空气动力学学报，2004，22（4）：490-493．

［17］YVES B．A finite element method study of eulerian dropletes impingement models［J］．International Journal for Numerical Methods in Fluids，1999，29（4）：429-449．

An efficient method to simulate water droplet trajectory and impingement

ZHOU Zhihong1，YI Xian1，GUI Yewei1，LI Fengwei2
（1.State Key Laboratory of Aerodynamics，China Aerodynamics Research and Development Center，Mianyang 621000，China；2.Aeronautics School，Northwestern Polytechnical University，Xi′an 710072，China）

Ice formation on aircraft is of great safety concern because icing may lead the aircraft to a dangerous situation quickly．Numerical method for determining the trajectories of the water droplets is the base of the icing research and the design of the anti-icing system．The traditional Lagrangian method for simulating water droplet trajectory and impingement has some shortages such as lower computation efficiency and poor applicability currency in peculiar geometry．In order to overcome these shortages，an improved Lagrangian method was developed．It′s based on the calculation of the flow field around icing surface，using a method of searching extended target to calculate the droplet location and determining the insert value of flow field information at the droplet location in a grid cell，the boundary of the droplet trajectories are judged based on a manage system of boundary information with framework structure．The method can overcome theses shortages meanwhile maintaines the robustness of original method．Local droplet collection and impingement efficiency at NACA0012 and multi-element airfoils are calculated with this method in order to verify its correctness．The results show that the improved method is very efficient，reliable，and robust．Furthermore，it can be used in different geometries directly．

ice；the trajectories of the water droplets；method for searching extended target；Lagrangian method

V211.3

Adoi:10.7638／kqdlxxb-2012.0179

0258-1825（2014）05-0712-05

2012-10-31；

2013-01-01

国家自然科学基金（11172314）；中国博士后基金（2012M512065）；四川省国际合作计划（12064HH0042）

周志宏（1981-），男，湖南省涟源人，博士，研究方向：计算流体力学、飞机结冰．E-mail：zhouzhihong029＠163．com

周志宏，易 贤，桂业伟，等．水滴撞击特性的高效计算方法［J］．空气动力学学报，2014，32（5）：712-716．

10．7638／kqdlxxb-2012．0179． ZHOU Z H，YI X，GUI Y W，et al．An efficient method to simulate water droplet trajectory and impingement［J］．ACTA Aerodynamica Sinica，2014，32（5）：712-716．