连续尺度变换方程在稳态及非稳态流动模拟中的应用

张 扬，白俊强，华 俊，徐晶磊

（1．西北工业大学航空学院，陕西 西安 710072；2．中国航空研究院，北京 100012；3．北京航空航天大学 能源与动力工程学院，北京 100191）

连续尺度变换方程在稳态及非稳态流动模拟中的应用

张 扬1，白俊强1，华 俊2，徐晶磊3

（1．西北工业大学航空学院，陕西 西安 710072；2．中国航空研究院，北京 100012；3．北京航空航天大学 能源与动力工程学院，北京 100191）

为了提高涡粘性假设的湍流模型对于非稳态流动的求解精度，同时兼顾其对于稳态流动的求解性能，将雷诺应力项与连续变换方程（CSSE）结合而形成新的应力项，使其根据流场尺度、网格尺度及Kolmogorov尺度来自动调节当地的应力雷诺应力模化水平，避免网格因素在流场模拟中产生不利影响，改正了混合RANS／LES方法的速度型偏离对数率问题；同时，该方法并未引入显式亚格子模型（SGS），因此回避了亚格子系数确定对于流场模拟精度产生的影响，改善了湍流模型对于流动不稳定性的辨识精度。在湍流平板算例中，CSSE方法计算的边界层速度型精度与雷诺平均方法（RANS）相当，而对于圆柱尾迹的模拟则证明了CSSE方法具有混合RANS／LES方法的优点，即能够准确模拟流动的不稳定性特征。

湍流模型；剪切应力；雷诺方程；混合RANS／LES方法

0 引 言

自然界中的流动大部分以湍流形态存在，湍流的精确求解仍然是一个开放的科学问题。虽然流动控制方程早已被Navier和Stocks提出，但是人们一直以来无法得到一种适合于各种流体的解析答案。湍流的Kolmogorov尺度伴随雷诺数的增长迅速减小，Pope［1］认为最小的空间尺度应是Kolmogorov尺度的2倍才能完全解析出流场的全部脉动，这引起直接数值模拟方法（DNS）所需要的网格数量巨大；同时，为了求解流场中小尺度脉动，所需时间步必须调至极其微小才能兼顾空间推进和时间推进。这些方面注定了DNS方法现在只能运用于低雷诺数简单流动，如槽道流动等［2］。DNS方法求解效率低下原因在于对于能谱耗散区域的直接模拟，假设流场中耗散尺度都为各项同性，可以将这些尺度对于流场的影响量以一种解析表达式给定出来，流场中其余尺度脉动采用直接求解，这种方法被称为大涡模拟（LES），该方法虽然在一定程度上降低了DNS方法的网格需求，在一些方面也有了一定的应用［3］。但随着雷诺数的提高，所谓的“大涡”也会减小为较小尺度的涡旋结构，因此该方法在高雷诺数的应用仍然存在一定的障碍。

雷诺平均方法（RANS）是求解N-S方程中最常用的统计平均方法，该方法通过模化流场的非定常效应来达到降低计算代价的目的，由于该方法流场脉动的空间尺度随时间的变化被平均运算抹平，因而面对附着流动等时间伴随性并不十分明显的流场求解可以获得满意的精度。从统计平均方面来说，流场脉动速度的统计值为零，但是在流场不稳定因素增多时，如大分离流动，脉动项会对速度场的平均项产生很大的影响，继而影响流场的动量输运作用，因此RANS方法在伴随分离的流动求解中精度较差。

为了获得求解效率与精度的平衡，学者们试图将RANS方法和LES方法进行混合，Spalart［4］等人发展了一种脱体涡模拟方法（DES），以一方程Spalart-Allmaras湍流模型［5］为基础，采用网格距离对原方程中的壁面距离进行变换，使得方程毁灭源项迅速增大，从而迅速降低当地的雷诺应力水平，将更多的脉动尺度释放出来。该方法已经得到了广泛的应用，Squres［6］在2002年的文献中，展示了对于C-130，F-16及F-15E的全机DES模拟；Saqib等人采用DES方法对涡流发生器进行了计算［7］；Shivaji等人采用DDES方法预测了三维的翼型失速过程［8］；国内的吴晶峰等人［9］采用DES方法对后台阶流动进行了计算，反映出该方法对于回流运动的精确捕捉；陈江涛等基于DES开展了综合应用分析［10］。

由于大分离流动中流动充分失稳，附面层内部的求解精度对于整体结果精度影响较小，但是在诸如翼型的抖振边界等小尺度分离流场中，DES方法所得结果通常过早失速，这主要由于尺度转换方程过于简单，引起网格加密过程中附面层内被LES侵入，当地脉动未被充分激发而导致雷诺应力迅速下降，引起当地速度型与壁面对数率不匹配，甚至引发当地出现非物理分离现象［11］，所以在稳态流动如平板流、槽道流动中无法得到满意的求解精度。

为了克服该缺点，本文以较常用的Menterk-ω SST［12］方程为基础进行改造，使其在保留稳态流动求解精度的同时，能够提高对于非定常流动的求解精度，形成一种对于流动失稳强度自适应的湍流模型。

1 湍流控制方程

目前在工程中主要以线性两方程湍流模型为主，两方程湍流模型主要面向的是两个基本量，即湍动能和耗散率，基于此发展出来了常用的k-ω［13］和k-ε［14］模型，而k-ε模型在附面层附近的模拟精度较差，因为湍流耗散率在附面层内数值极小，对网格要求比较苛刻；而Wilcox［13］提出的k-ω方程虽然改善了近壁模拟精度，但是对于自由来流条件极为敏感。Menter［12］提出基于k-ω方程的剪切应力输运模型，将两者的优点通过混合函数结合起来，附面层附近采用k-ω方法，远壁面位置采用k-ε方法，保留了两种方法各自的优点。其方程形式为：

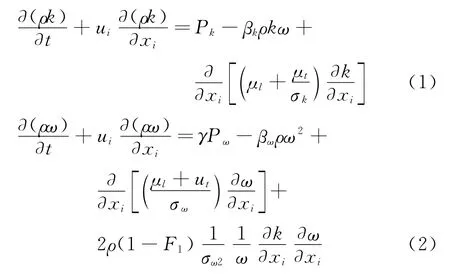
其中Pk和Pω分别为湍流生成项，表达式为：

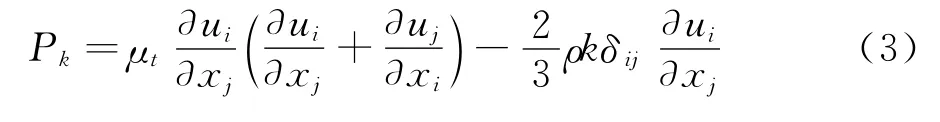
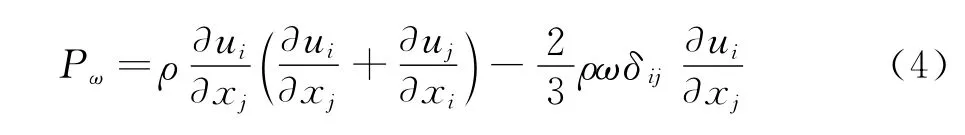
模型中的Cω、σk、σω、β、F1、F2均为常数和特定的函数表达式，其数值和处理方法采用文献［12］中的做法。最终，在剪切应变率模型中涡粘性系数表达式为：

其中a1＝0.3，Ω为涡量，其张量形式为：Ω＝0.5（Ui，j－Uj，i），Ui，j和Uj，i为速度导数的张量。

为了与DES方法对比，本文在算例中同时引入了SST-DES方法进行验证，上述SST湍流模型中湍流尺度lk-ω表达式为：

将湍流尺度lk-ω替换为min（lk-ω，CDESΔ），其中Δ为网格三个方向的最大边长，常数CDES＝0．78，这样便形成了SST-DES［15］方法，具体做法可以参考文献［15］。

2 基于连续尺度变换函数的应力方程

以线性涡粘假设为背景的SST湍流模型对于雷诺平均后产生的不封闭项采用Boussinesq假设关系式获得，但是该过程容易对涡粘性产生过高估计，加之时均效应对流场中的中小尺度脉动会造成强烈的压制，总体上难以反映流场的中高频脉动变化过程，在雷诺平均动量方程中，需要进行建模求解的目标量为湍流剪切应力τRANSij，该项表征着湍流脉动引起的动量通量输运，一般通过Boussinesq提出的涡粘性理论进行求解，该理论假设湍流应力和平均应变率张量中存在一种线性关系，即：

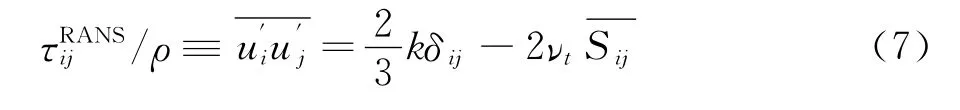
其中u′i为湍流脉动速度，k为湍动能，δij是Kronecher Delta符号（若i＝j，则δij＝1；若i≠j，则δij＝0），结合式（3），可以得到以下结论：

Batten［16］等人曾经提出过一种数值限制尺度模型（LNS），该方法通过一个调整因子将湍流模型的生成项降低来削减当地的雷诺应力水平；Spalart等人的DES方法则是将湍流模型的耗散项增大来达到同样的目的。这两种思路是一种湍流求解尺度转换思想，如DES方法中，壁面距离被式（9）代换：

在本文中，为了避免网格诱导分离现象的产生，同时将流场尺度切换函数变得更为光顺，引入连续型变换因子ZR，令ZR∈（0，1），并将雷诺应力改写为：

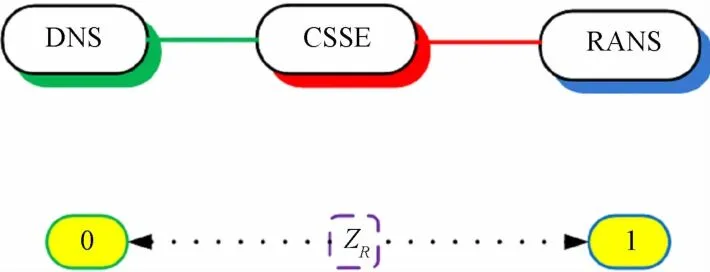
图1 连续尺度变换方法与DNS和RANS方法关系Fig.1 Relationship between CSSE，DNS and RANS

区别于DES方法的是，CSSE方法并未引入显式的亚格子模型方程，避免了亚格子系数的不同而导致RANS和LES区域分割不同。

3 连续变换因子ZR的推导

在湍流能量谱中，湍动能高波段代表湍流耗散区，该区域的湍流尺度通常位于网格分辨尺度以下，对于该区域在LES方法中通常采用亚格子模型模化，将一定波数以上的脉动采用关系式模化以此来反映高频脉动对于其他频段脉动影响，其他波数则直接求解，而将直接求解与模化求解的分界线定义为截断波数κc，从图2中可以看出，κc位于湍动能谱惯性子区，考虑到Kolmogorov的－5／3次方率，同时湍动能谱函数、湍流耗散率以及波数之间有如下估计：

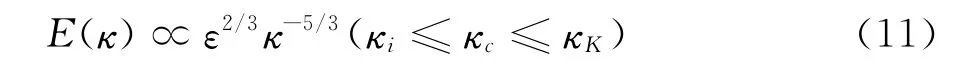
κi和κK分别代表了湍流积分尺度和Kolmogorov尺度对应的波数。

从本质上讲，除DNS方法外，其他湍流模拟方法仍是一个以截断波数为界线的分区问题，以此为基础构造连续变换因子ZR，定义：

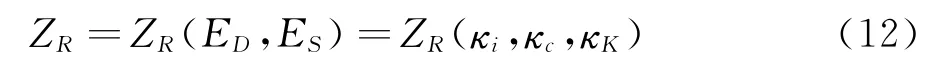
其中ED和ES分别代表直接求解的湍动能和模化求解的湍动能，将式（12）重新写为：

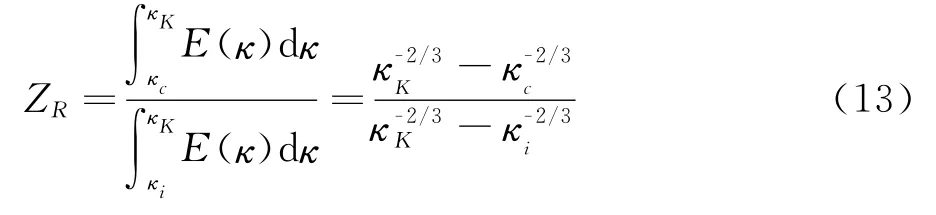
为了保证数值稳定性，令κc＝max（κi，min（κK，κc））来保证ZR的上下限。由于波数κ在求解中不能直接得出，需要将其转换为湍流的尺度量，引入波数与湍流尺度的关系式，可以得到：

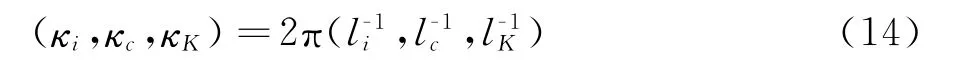
联立式（13）与式（14），将转换因子写为：

其中：lK＝（ν3／ε）1／4，li＝Cμk3／2／ε，根据Nyquist采样定律（如尺度为Δ的网格是无法解析尺度小于2Δ的流场脉动），故定义lc＝2Δ＝2（ΔxΔyΔz）1／3，Δx、Δy和Δz分别代表了当地网格在三个方向的法向长度（采用网格体积除以三个方向投影面积获得）。

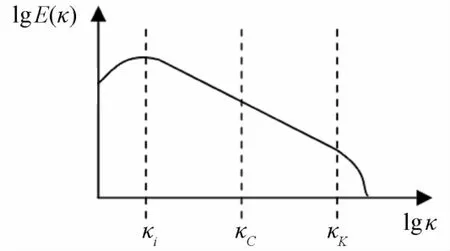
图2 各个尺度在能谱中的位置Fig.2 The locations of each scale at energy spectrum

4 算例验证及分析

4.1 平板边界层流动模拟

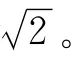
从图3反映的速度型分布可以看出，由于该网格当初是为高雷诺数的RANS方法模拟设计，仅仅是为了取得精确结果而进行了一定程度的加密，DES方法的结果过早上扬，证明了该方法给出的当地涡粘性系数下降过低，说明DES方法在当地已经开始采用LES方法进行模拟而削减了当地的雷诺应力水平，而CSSE方法与RANS方法与Spalding理论解十分贴近，证明CSSE方法在附面层内确实能够表现出完全的RANS特征，因此该方法对于稳态流动的鲁棒性要高于DES方法。

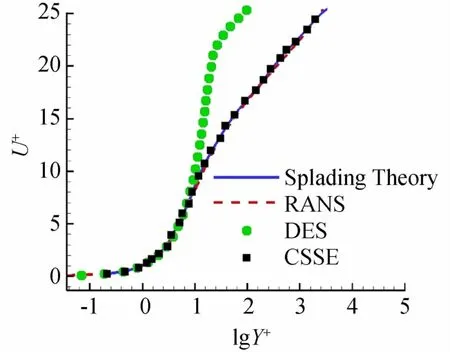
图3 平板边界层速度型Fig.3 Velocity pr of ile of flat plate boundary

4.2 圆柱尾部非稳态流动模拟

圆柱作为经典的钝头体模型，经常被用来验证非稳态流动的特征，因为圆柱即使在很低的雷诺数下仍可以产生明显的流动分离现象和涡旋结构。

本算例采用一个处于亚临界区域的圆柱试验进行模拟，实验雷诺数Re＝3900。该雷诺数下是一个层湍共存区域，由于SST湍流模型并未引入转捩识别模型，所以基于全湍假设的RANS方法对于该区域的模拟精度并不理想，采用该算例更能说明RANS、CSSE和DES方法的预测精度。

试验数据采集自Lourenco［17］等人的试验，圆柱参考长度为直径D＝0．01m，计算域如图。

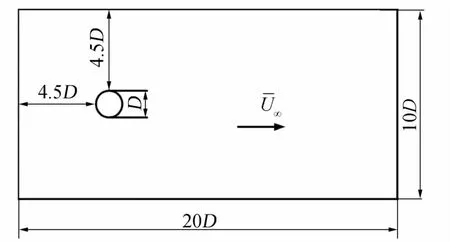
图4 圆柱绕流计算域Fig.4 Computation domain of flow over circle cylinder

为了使圆柱展向流动充分发展，展长给定为πD，保证第一层网格y＋＜1以尽可能的描述小尺度脉动。该网格规模约为130万，采用多块结构网格方便并行分区计算分区。计算域入口给定速度型入口，上顶、地板和左右壁面设定为对称边界条件，出口给定压力出口。图5为网格示意图。

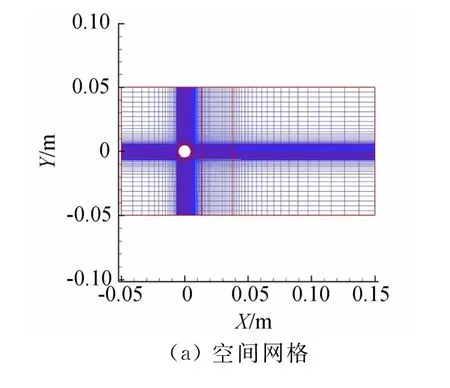
图5 圆柱空间和表面网格Fig.5 Space and surface mesh of cylinder

图6为圆柱升力和阻力系数随时间发展的变化，CSSE和DES方法都反映出了一种无规律的振荡特性，该现象体现了圆柱尾迹中非稳态流动中各尺度脉动相互影响，中小尺度脉动的高频振荡使得力系数的振荡峰值各不相同。

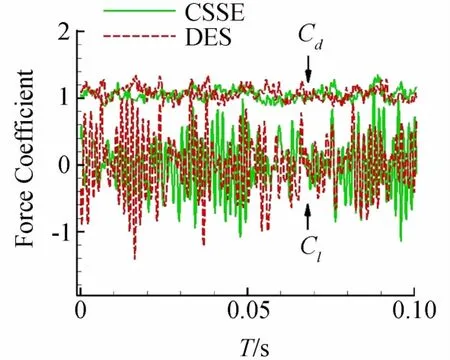
图6 力系数随时间变化历程Fig.6 Time history of force coefficient

从图6观察可知，两种方法所得升力系数基本在0附近振荡，阻力系数在1．1附近振荡，从Lourenco的试验中采集得到的阻力系数Cd为0．99，证明CSSE方法在非稳态流动中的求解精度相当于DES方法。

图7和图8分别为两种方法的Q值为20时的云图，Q准则是Hunt［18］等人为了反映非稳态流场中的瞬时相干结构而发明的一种可视化准则，Q准则可以清晰的反映流场中的涡旋结构。从图8中可以看出，CSSE方法在释放流场涡旋结构方面基本等同于DES方法，这反映了该方法的类LES特征，说明连续尺度变换方程在远离附面层后迅速削减了当地雷诺应力水平，即保证了附面层内的稳态流动求解，也兼顾了非稳态流动的求解精度。

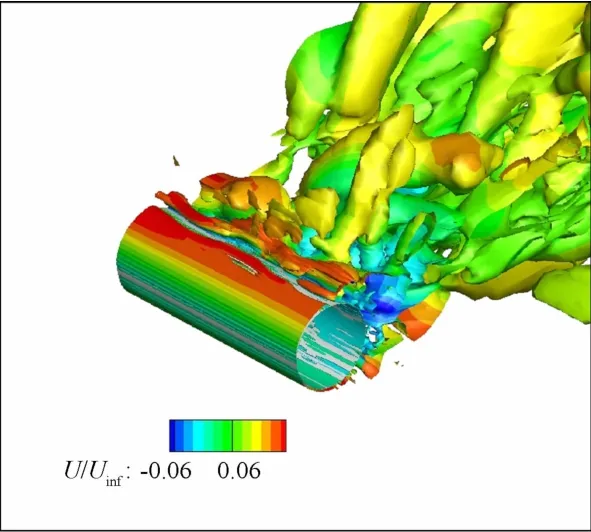
图7 DES方法计算的Q云图Fig.7 Q contour of DES method

图8 CSSE方法计算的Q云图Fig.8 Q contour of CSSE method

图9为平均后的圆柱表面压力系数分布，CSSE和DES方法所预测的压力系数与试验数据形态基本一致，压力拐点吻合的较好，而RANS方法在压力拐点后的逆压梯度远大于试验值，说明RANS方法对于回流区预测过长。

图10分别为X／D＝1．06、1．54和2．02站位的速度型，可以看出，CSSE方法在近壁区域和远壁区域的预测精度均与试验值吻合，具有良好的鲁棒性。

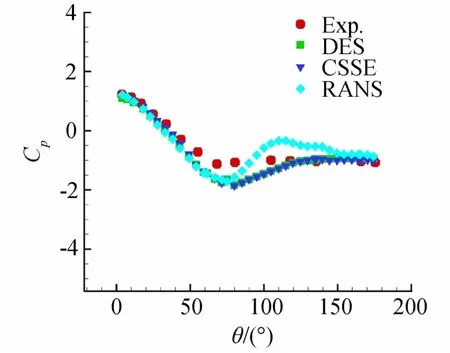
图9 圆柱表面压力系数Fig.9 Cpof cycle cylinder surface

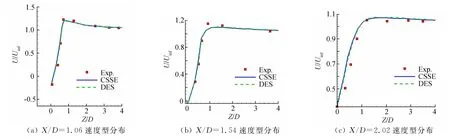
图10 圆柱不同切面速度型Fig.10 Velocity pr of ile at different slice of cylinder

5 结束语

本文通过一种连续尺度变换方程，将原始SST方程涡粘性系数重新构造，使其变换为一种流场尺度自分辨方法，通过理论分析和算例验证，取得了以下结果：

（1）提出了一种基于连续变换方程的湍流模拟混合方法，通过理论分析证明该方法可以在DNS和RANS间自动进行切换；

（2）构造了一种连续变换因子，除了当地网格尺度外，该因子还依赖流场中的惯性尺度以及Kolmogorov尺度，避免了混合RANS／LES方法对于网格的严重依赖性；

（3）基于平板边界层模拟，证明CSSE方法在稳态流动中可以保持良好的RANS特性，阻止附面层内的雷诺应力过度损耗，保持正确的附面层内速度型分布；

（4）通过圆柱绕流尾部的非稳态流动模拟，证明CSSE方法有类LES方法特征，可以有效的缓解RANS方法对于高波数段脉动的压制，其流场仿真精度基本等同于LES方法，说明这是一种新型的混合RANS／LES方法；同时，由于CSSE方法并未引入显式的亚格子模型，因此摆脱了传统混合RANS／LES方法中亚格子常数对于求解精度的影响问题。

［1］POPE S B．Turbulent flows［M］．London：Cambridge University Press，2000：231-232．

［2］JOHN K，PARVIZ M，ROBERT M．Turbulence statistics in fully developed channel flow at low Reynolds number［J］．Journal of Mech．，1987，177：133-166．

［3］PIERRE S．Large eddy simulation for incompressible flows［M］．Berlin：Springer Press，1998：131-132．

［4］SPALART P R，JOU W H，STRELETS M，et al．Comments on the feasibility of LES for wings and on a hybrid RANS／LESapproach［M］．Los Angles：Greyden Press，1997．

［5］SPALART P R，ALLMARAS S R．A one equation turbulence model for aerodynamic flows［J］．RecherchéAerospatiale，1994，1：5-21．

［6］SQUIRES K D，FORSYTHE J R，MORTON S A．Progress on Detached Eddy Simulation of massively separated flows［R］．AIAA 2002-1021．

［7］SAQIB M，ROLF R．Detached-Eddy Simulation of vortex generator jet using chimera grids［J］．World Academy of Science，Engineering and Technology，2011，79：732-739．

［8］SHIVAJI M，JAMES D B．Numerical investigation of 3-D dynamic stall using delayed detached eddy simulation［R］．AIAA 2012-0099．

［9］WU J F，NING F F．Hybrid RANS／LES method applied to backward facing step［J］．Journal of Beijing University of Aeronautics and Astronautics，2011，6（1）：32-37．（in Chinese）

吴晶峰，宁方飞．后台阶流动的Hybrid RANS／LES模拟［J］．北京航空航天大学学报，2011，6（1）：32-37．

［10］CHEN J T，ZHANG P H，ZHOU N C，et al．Application of Detached-Eddy Simulation based on Spalart-Allmaras turbulence model［J］．Journal of Beijing University of Aeronautics and Astronautics，2012，7（38）：2-5（in Chinese）

陈江涛，张培红，周乃春，等．基于SA湍流模型的DES方法应用［J］．北京航空航天大学学报，2012，7（38）：2-5．

［11］MENTER F R，EGOROV Y．Re-visting the turbulent scale equation［C］．In：Proc．IUTAM Symp．One Hundred Years of Boundary Layer Research．Springer，Gottingen，2004．

［12］MENTER F R．Two-equation eddy-viscosity turbulence models for engineering applications［J］．AIAA Journal，1994，32（8）：1598-1605．

［13］WILCOX D C．Reassessment of the scale-determining equation for advanced turbulence models［J］．AIAA Journal，1988，26（11）：1299-1310．

［14］JOHNSON D A，KING L S．A mathematically simple turbulence closure model for attached and separated turbulent boundary layer［J］．AIAA Journal，1985，23（11）：1684-1692．

［15］STRELETS M．Detached Eddy simulation of massively separated flows［R］．AIAA 2001-0879．

［16］BATTEN P，GOLDBERG U，CHAKRAVARTHY S．LNS-an approach towards embedded LES［R］．AIAA2002-0427．

［17］LOURENCO L M，KROTHAPALLI A．Application of DPIV to the study of the temporal evolution of the flow past a circular cylinder［J］．Laser Anemometry in Fluid Mech．，1988：161-177．

［18］HUNT J，WRAY A，MOIN P．Proceedings of the 1988 summer program［R］．Stanford：Center for Turbulence Research，1988．

Application of a continuous scale switch equation in steady and unsteady flow simulation

ZHANG Yang1，BAI Junqiang1，HUA Jun2，XU Jinglei3
（1.School of Aeronautics，Northwestern Polytechnical University，Xi′an 710072，China；2.Chinese Aerodynamic Establishment，Beijing 100012，China；3.School of Energy and Power Engineering，Beihang University，Beijing 100191，China）

In order to get the higher precision of the unsteady flow predicted by using liner turbulence model as well as keep the capability of solving the steady flow，the Reynolds-stress term is combined with continuous scale switch equation（CSSE）to form one new stress term which can automatically adjust the local Reynolds-stress level according to the flow field scale，grid scale and Kolmogorov scale．The CSSE method eliminates the disadvantage of grid scale on the flow simulation，the problem of disagreement between the velocity pr of ile obtained by the method of hybrid RANS／LES and the law of the wall is solved．Meanwhile，this method do not use the explicit sub-grid stress（SGS）model which can avoid the disadvantaged impact on the flow simulation caused by SGS coefficient，so the flow instability can be controlled more accurately．The simulations of the boundary flow of the plate and the flow over the cylinder both prove that CSSE method is robust．In the testcase of a turbulent flat-plate，the velocity pr of iles of flat-plate boundary layer solved by CSSE match with that solved by Reynolds averaged Navier-Stocks（RANS）method very closely，the simulation of cylinder wake proves that the CSSE method can precisely simulate the flow instability which is the advantage of hybrid RANS／LES．

turbulence model；shear stress；Reynolds equation；hybrid RANS／LES method

V211

Adoi:10.7638／kqdlxxb-2012.0197

0258-1825（2014）05-0694-06

2012-11-26；

2013-03-28

国家自然科学基金（11002014）

张扬（1988-），男，陕西西安人，博士研究生，研究方向为工程湍流模拟．E-mail：iamvip2＠163．com

张扬，白俊强，华俊，等．连续尺度变换方程在稳态及非稳态流动模拟中的应用［J］．空气动力学学报，2014，32（5）：694-699．

10．7638／kqdlxxb-2012．0197． ZHANG Y，BAI J Q，HUA J，et al．Application of a continuous scale switch equation in steady and unsteady flow simulation［J］．ACTA Aerodynamica Sinica，2014，32（5）：694-699．