结构误差对旋转稳定弹丸气动特性影响的数值模拟
2014-04-30陈东阳LaithAbbas芮筱亭王国平
陈东阳,Laith K.Abbas,芮筱亭,王国平
(南京理工大学 发射动力学研究所,江苏 南京 210094)
结构误差对旋转稳定弹丸气动特性影响的数值模拟
陈东阳,Laith K.Abbas,芮筱亭,王国平
(南京理工大学 发射动力学研究所,江苏 南京 210094)
基于剪切应力传输(SST)k-ω湍流模型,对考虑结构误差情况下的弹箭模型进行数值模拟计算。首先采用CFD和工程经验公式相结合的方法,得到了不同马赫数、不同转速情况下无结构误差模型的多种气动特性参数。通过与实验数据对比,阻力、法向力、俯仰力矩、压心位置误差在10%以内,验证了该方法的可行性和准确性。然后,建立了考虑结构误差即质量分布不对称、弹体不同轴和无结构误差模型,并分别进行了气动特性模拟计算。结果表明,质量偏心对滚转阻尼力矩系数、马格努斯力矩系数影响很大;弹体不同轴对法向力系数导数、俯仰力矩系数导数、马格努斯力矩系数导数和压心位置都产生很大影响。结构误差使模型的多种气动特性参数产生很大变化,将影响其飞行弹道和稳定性。
结构误差;湍流模型;计算流体力学;旋转
0 引 言
在弹箭的生产制造过程中,由于设备、工艺以及技术水平等诸多因素的影响,弹箭结构总会和理论设计的有一定的偏差。对于弹箭,主要的结构误差有弹体质量分布不均匀导致的质量偏心、由于安装误差导致的弹体不同轴、翼面安装角误差等。这些误差对高速飞行弹箭的气动特性和飞行稳定性都会带来影响。因此,对弹箭气动参数的准确获取和对结构误差可能带来的气动特性影响进行精确仿真分析,十分必要。随着计算机的发展和数值模拟软件的计算能力的提高与完善,采用数值计算方法获取飞行器气动数据成为可能。相对于风洞实验和工程估算,CFD仿真有其特有的优势。CFD仿真可以很好的预测复杂几何体的气动特性参数和流体流动现象[1-5],可以模拟风洞实验无法模拟的条件,并且可以减少实验次数,大大节省设计成本。表1[6]给出了三种方法预测气动力的误差统计结果。其中飞行试验预测气动力的结果要好于风洞实验和工程程序。文献[7]基于CFD技术,比较了RNGk-ε、k-εRealizable、DES等湍流模型的计算结果,证明了CFD程序有很高的计算精度,甚至有时可以代替飞行试验,为飞行器弹道计算、飞行控制提供准确气动特性数据。

表1 空气动力系数的预估误差(%)[6]Table 1 Expected aerodynamic coefficient percent errors
本文采用基于SST湍流模型的高精度CFD技术,和高质量的网格生成方法对M910旋转弹丸模型进行数值计算,获得模型的各种气动参数并与实验数据比较,来验证该数值方法的可行性与准确性。然后通过对带有结构误差的两种模型采用同样的数值方法进行数值模拟计算,精确获得其各种气动参数,然后分析结构误差对旋转弹丸模型气动特性,飞行弹道和稳定性可能带来的影响。网格划分软件为ICEMCFD,流体解算器为Fluent。
1 几何模型
选用M910旋转稳定弹丸为假设的模型,几何参数、飞行速度、旋转速度等参数详见文献[7]。本文建立了三种几何模型即无结构误差模型、质量偏心模型、不同轴模型。如图1~图3所示。假设质心相对无结构误差模型的质心向右平移了1mm,如图2所示。如图3所示,弹体轴线相对无结构误差模型做了不同轴假设,使弹头处向下偏转了2°。
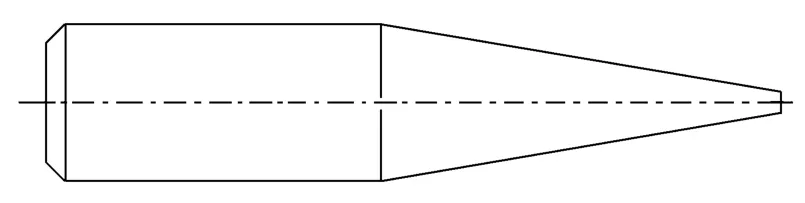
图1 无结构误差的模型Fig.1 Model without structure errors
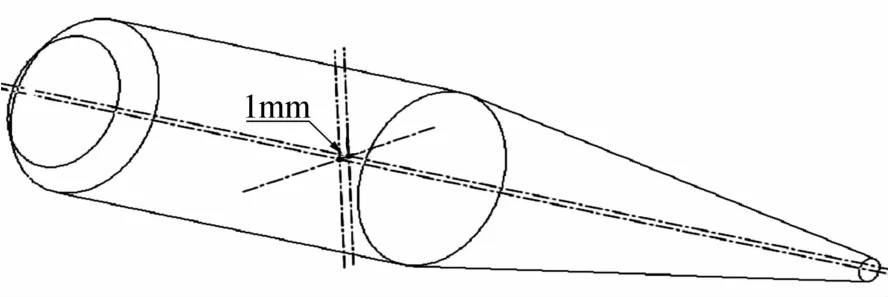
图2 有质量偏心误差的模型Fig.2 Model with mass asymmetry errors
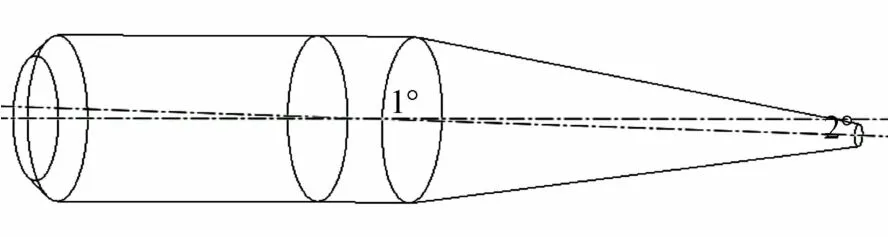
图3 有同轴误差的模型Fig.3 Model with coaxial error
2 计算方法
2.1 计算流体力学控制方程和湍流模型
控制方程通用形式[8]:

式中:φ为通用变量,可代表速度、温度等求解变量;Γ为广义扩散系数;S为广义源项。
式(1)中各项依次为瞬态项、对流项、扩散项和源项。表2给出了三个符号与各特定方程的对应关系。
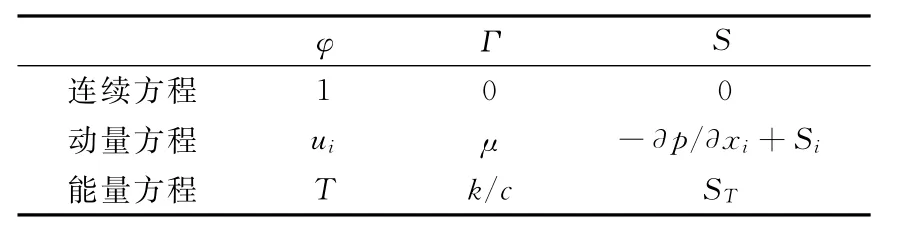
表2 通用控制方程中各符号的具体形式Table 2 Specific expressions of three parameters in general control equation
对于湍流,如果直接求解高度非线性的三维瞬态N-S方程,需要采用对计算机内存和速度要求很高的直接模拟方法,目前还不可能在实际工程中采用此方法。工程上对瞬态的N-S方程做时间平均处理,得到雷诺平均的NS方程(RANS):
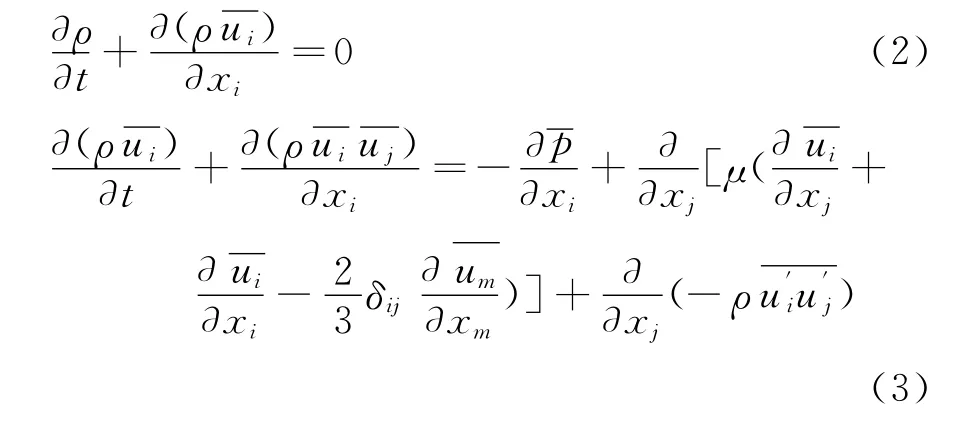
其中:
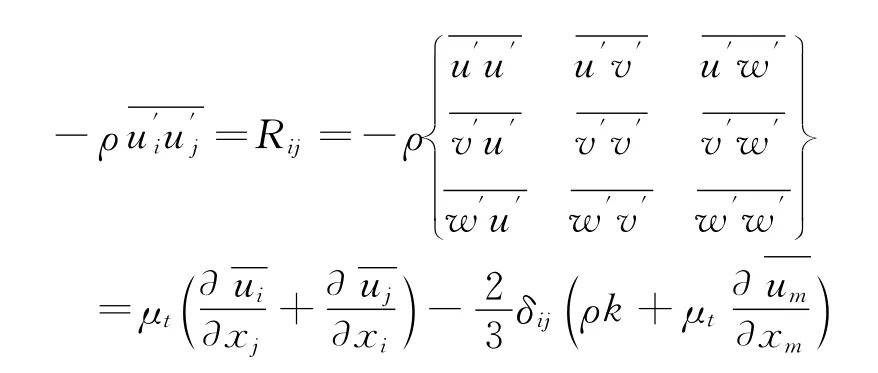
本文选用涡粘模型(EVM)中的SSTk-ω湍流模型[9],它结合了在边界层内能很好模拟低雷诺数流动的标准k-ω湍流模型,在边界层外能很好模拟完全湍流流动的k-ε湍流模型的优点。其间通过一个混合函数来过渡,属于两方程涡粘性模式。k和ω的输运方程如下所示:
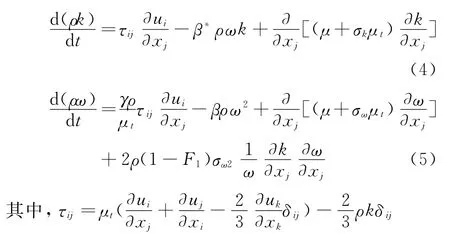
混合函数
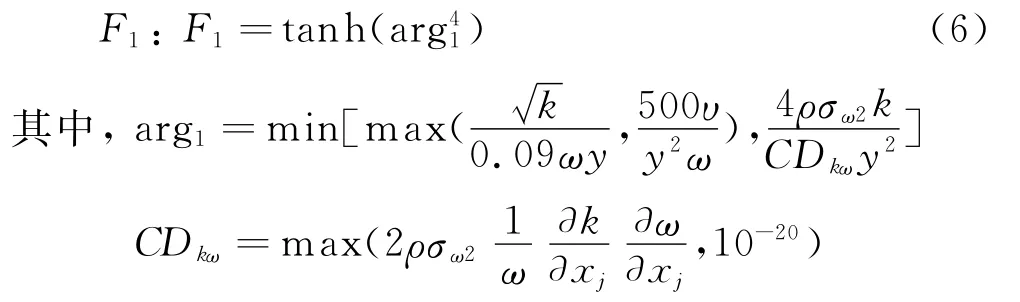
其中涡粘系数定义为:

其中Ω是涡量的绝对值。
混合函数F2定义为:
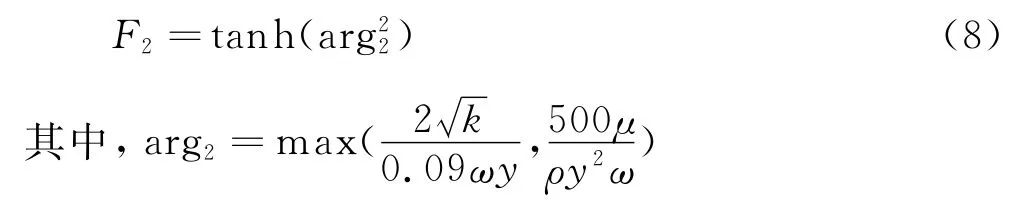
SST湍流模型中常数通过式(9)混合:
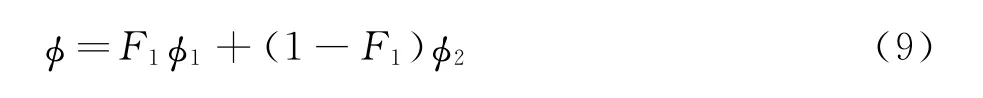
其中集合(φ1)代表标准的k-ω湍流模型中的常数,集合(φ2)代表标准的k-ε湍流模型中的常数。

2.2 边界条件与数值格式
远场边界按黎曼不变化无反射条件来处理,在物面上采用无滑移条件来处理,对计算模型设置壁面旋转。采用基于有限体积法的AUSM格式进行空间离散,AUSM兼有Roe格式的间断高分辨率和Van Leer格式的计算效率高的优点。在对流项,湍流粘性项采用二阶迎风格式。同时,采用隐式时间离散格式,对于超声速粘性流动,物体近壁面处的流场会产生急剧的变化,因此在近壁面处和激波处需要加密网格。
2.3 计算网格
流体与壁面间相互作用,很多因变量具有较大的梯度,而且粘度对传输过程有很大的影响。k-ω模型(包括SST模型)采用的是自动壁面函数,即可以在近壁处,将壁面函数自动调整为低雷诺数壁面方程。一般k-ω模型要求近壁处有y+<5[10]。为了准确模拟滚转阻尼等系数。在边界层内对网格进行加密,保证y+≤0.5,以保证边界层内有十层以上的网格。本文采用多Block生成流场拓扑结构、外O Block生成弹体边界层的方法,生成了高质量的结构化网格。
为了减小计算量,将每套网格数量都压缩在50万左右,仅为文献[7]网格数量的1/3~1/2。但通过提高网格质量,保证了计算精度。由于来流速度范围较大,流场均分别采用两套计算网格。部分流场拓扑结构如图4、图5所示,部分流场计算网格如图6、图7所示。

图4 不同轴模型流场拓扑图(Ma>1.3)Fig.4 Fluid field topology graph of the model with coaxial error(Ma>1.3)

图5 不同轴模型流场拓扑图(Ma<1.3)Fig.5 Fluid field topology graph of the model with coaxial error(Ma<1.3)

图6 无结构误差模型流场计算网格(Ma>1.3)Fig.6 Flow field grid of the model without structure errors

图7 不同轴模型流场网格剖面图Fig.7 Pr of ile of flow field grid of the model with coaxial error
3 计算公式
CFD求解气动特性参数的原理是,先对流场进行求解,得到流场每一个网格上的速度、密度、压力等参数,然后求出气动系数。
动稳定性导数简称动导数,是飞行器弹道计算和飞行控制所不可缺少的原始气动参数。对于外形简单,小攻角的弹箭可采用CFD与经验公式结合的方法[11-12],基于SST湍流模型,较好地计算了旋转弹的滚转阻尼等系数。
类似于风洞自由滚转技术原理公式[11],假设弹绕x轴以定角速度ωx做匀角速度旋转,则有:

其中,Cl0为弹箭无滚转时的滚转力矩。Cl为气动滚转力矩,以保证弹体做匀角速度旋转,由定常的CFD方法求出。Jx表示模型在滚转方向上的惯性矩。由上式推导出滚转阻尼力矩系数:
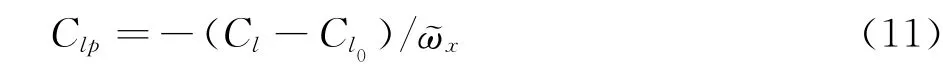
同理:俯仰阻尼力矩系数:
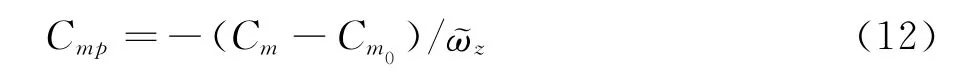
马格努斯力矩系数:

对于本文的光弹体计算模型,Cl0、Cm0、Cn0的值都为零。
马格努斯力系数导数公式:

法向力系数导数公式:

马格努斯力矩系数导数公式:

俯仰力矩系数导数公式:

4 结果与分析
对三种模型分别进行了数值模拟计算,马赫数分别为0.6、0.9、1.2、1.4、2、2.5、3.5、4.5,攻角为3°。图8~图11给出了Ma为2,攻角为3°时,流场速度云图、压力云图、密度云图和绕弹体的流线图。从图8~图10可以看出头部和尾部形成了清晰的斜激波在弹肩和弹底部区域形成了低压区。
由于存在攻角,模型周围的压力和密度在弹轴两侧不对称。弹体下方压力值和密度值高于弹体上方。从图11可以看到绕弹体周围速度流线图,图中显示出在弹底部形成许多涡旋。这些激波和涡旋形成的波阻和涡阻给弹体增加了阻力。仿真结果符合空气动力学规律。

图8 速度云图Fig.8 Velocity contour
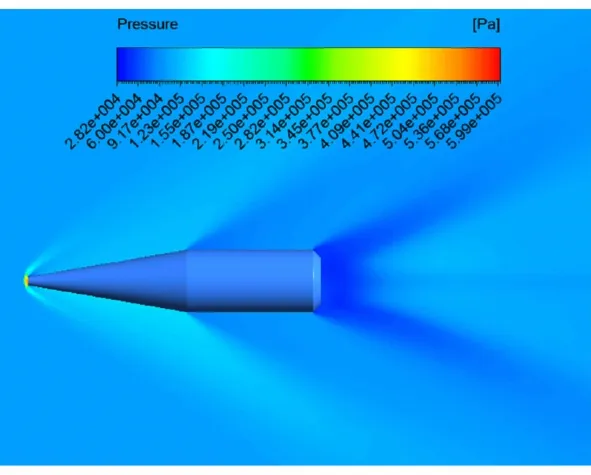
图9 压力云图Fig.9 Pressure contour
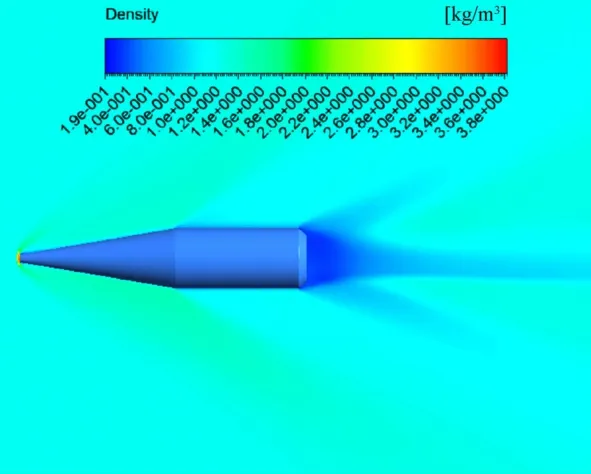
图10 密度云图Fig.10 Density contour
图12~图14为马赫数2、攻角为3°时,x=0.05m处的横截面上速度矢量云图,压力等值线云图和纵截面上的速度矢量云图。从图12、图13看出,边界层内速度矢量分布和横截面压力等值线分布不对称,这是有攻角的弹体高速旋转造成的,也是马格努斯力产生的原因。图14中也可以看到,贴近壁面处的速度矢量是弹体旋转的方向,然后渐变为轴向方向,说明模拟精度较高。
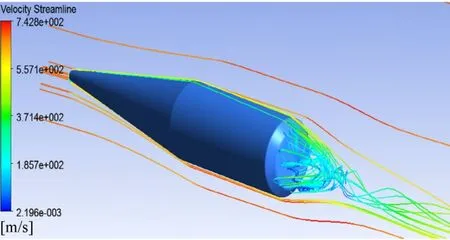
图11 流线图Fig.11 Streamline contour
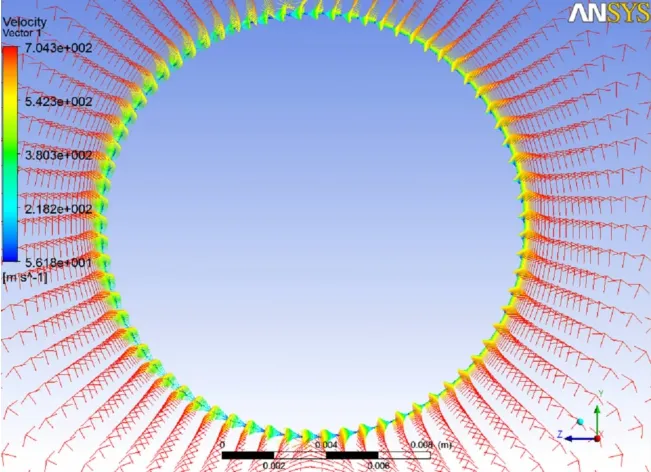
图12 x=0.05m处横截面速度矢量图Fig.12 Section of velocity vector contour at x=0.05m
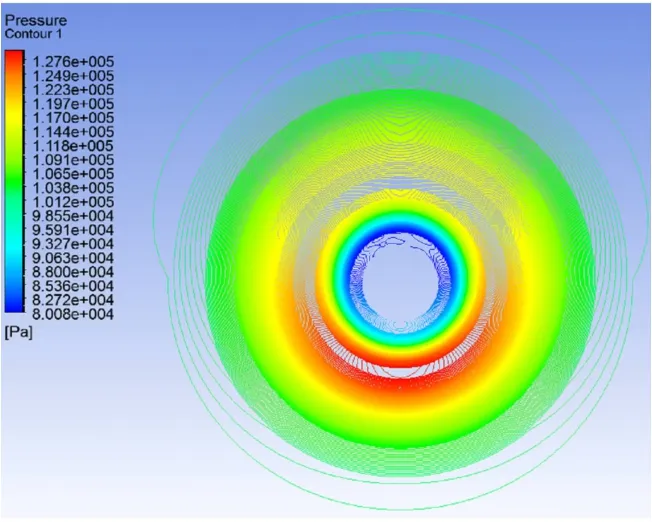
图13 x=0.05m处横截面压力等值线图Fig.13 Section of pressure contour at x=0.05m

图14 纵截面速度矢量图Fig.14 Longitudinal section of velocity vector contour
图15为CFD结果与PRODAS软件计算结果以及试验结果的比较,其中模型实验数据来自文献[7],从图15可以看出基于SST湍流模型的CFD数值模拟能力要比PRODAS软件模拟结果更好。
阻力系数、法向力系数导数、俯仰力矩系数导数误差均在15%以内。滚转阻尼系数误差在20%以内,误差都在工程计算误差范围内,但是对于马格努斯力矩系数导数,在超声速部分模拟较好,在亚声速和跨声速部分模拟误差比较大。两方程涡粘模型不能满足模拟要求。
此时,对于马格努斯力矩系数导数的计算,湍流模型需要采用大涡模拟或者分离涡模型模拟效果较好[5,7]。这些非定常的计算方法所需的计算机资源过大、时间太长,对计算机的硬件性能和内存资源都有很大的需求。从图15看出,阻力系数在跨声速处为极值,符合气动特性规律。由于平衡状态下模型滚转阻尼力矩与给定平衡的力矩方向是相反的,所以滚转阻尼系数值为负值。压心位置计算时选用弹径为参考长度。压心位置随马赫数的变化趋势如图15(f)所示,和实验数据对比,误差较小。
图16为无结构误差模型、质量偏心模型、不同轴模型的气动特性参数计算结果比较图。从图16(a)看出,质量偏心对计算模型的阻力几乎没有影响,说明阻力的大小只和模型外形有关,与质心偏移几乎无关。不同轴模型在亚声速和跨声速部分,阻力系数比无结构误差模型大,在超声速部分阻力系数比无结构误差模型小。最大误差达到15%,发生在亚声速处。这是由于模型不同轴时,导致模型外形改变,摩阻、涡阻、波阻都有所改变所造成的。
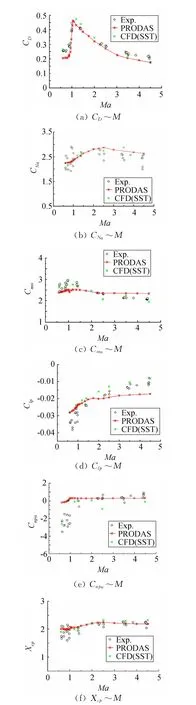
图15 气动特性随马赫数的变化Fig.15 Effect of Mach numbers on aerodynamic characteristics
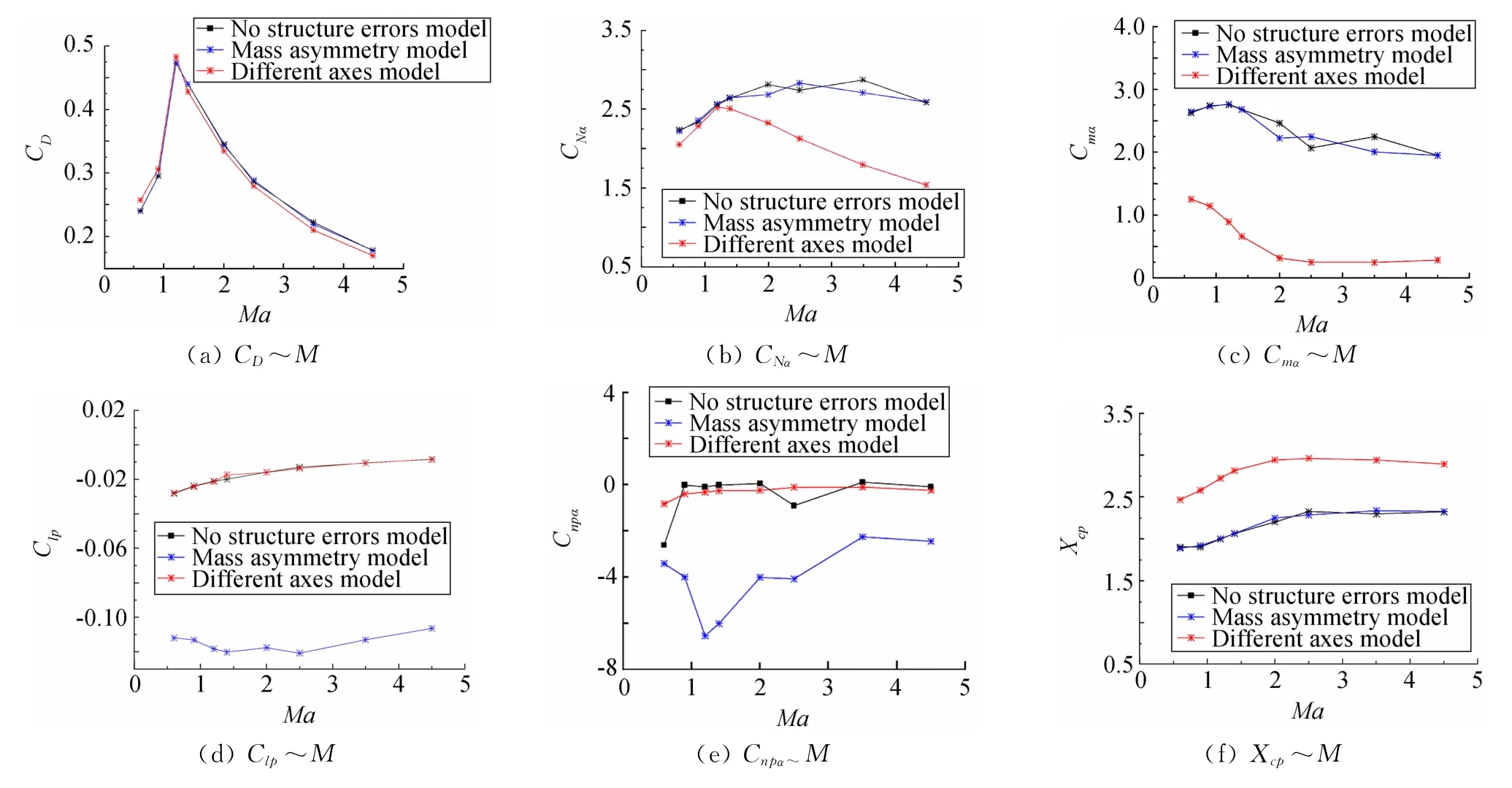
图16 三种模型气动特性的比较Fig.16 Comparision of aerodynamic characteristics of three models
图16(b)为三种模型的法向力系数导数随马赫数变化趋势。对于质量偏心模型,导致旋转轴线偏移,在亚声速和跨声速部分,计算结果和无结构误差模型结果一致;在超声速时,使法向力系数导数相对无结构误差模型的计算结果产生一些波动。由于不同轴模型的弹头处攻角相对理论模型变小,从而导致法向力系数导数比无结构误差模型计算结果小,并且随着马赫数的增大,法向力系数导数下降趋势变大,最大误差达到80%。质量偏心导致的旋转轴偏移和不同轴导致的外形改变对弹的法向力有一定影响,尤其是外形的改变对法向力影响很大。
从图16(c)看出,不同轴模型对俯仰力矩系数导数影响很大,最大误差达到91%,这是由于不同轴模型对法向力系数影响很大造成的。从图16(d)可以看出,质量偏心导致的旋转轴偏移,从而导致滚转阻尼系数变化很大,最大误差已超过100%。而不同轴导致的外形微小改变对滚转阻尼系数几乎没有影响。马格努斯力矩的产生和攻角、旋转有关。图16(e)可以看出,不同轴导致的弹头部攻角改变,和质量偏心导致的旋转轴偏移,都会对马格努斯力矩系数导数产生了较大影响,尤其是质量偏心的情况,对马格努斯力矩影响更大,使马格努斯力矩系数导数绝对值整体变大,最大误差超过100%。从图16(f)可以看出,主要是不同轴导致的弹体外形变化对压心位置影响很大,最大误差为40%。
旋转稳定弹飞行稳定性必须满足陀螺稳定条件和动态稳定条件[14-15]。其中陀螺稳定因子与弹的几何尺寸、飞行速度、自转速度、极转动惯量、赤道转动惯量、俯仰力矩系数导数、马格努斯力系数导数有关。动态稳定性条件与陀螺稳定因子、马格努斯力矩系数导数、俯仰阻尼系数导数、阻力系数、法向力系数导数、弹道倾角、重力加速度有关。从本文计算结果发现,三种模型的马格努斯力矩系数导数,俯仰力矩系数导数,法向力系数导数差异很大,所以结构误差对旋转弹的飞行稳定性和飞行弹道将造成很大影响。
5 结 论
通过计算结果比较分析,采用本文生成的低数量、高质量结构化网格,基于SST湍流模型边界层内外的优点,保证y+≤0.5,并与工程经验公式相结合的方法,可以较快的并保证精度的计算出各种复杂的气动特性参数。两种结构误差对气动特性参数都有影响,主要表现在质量偏心对滚转阻尼力矩系数,马格努斯力矩系数影响很大;弹体不同轴对法向力系数导数,俯仰力矩系数导数,马格努斯力矩系数导数和压心位置都产生很大影响。由于对这些气动特性参数产生的很大影响,将对弹箭飞行稳定性和飞行弹道产生很大影响。
参考文献:
[1]WU J,GU Z Q,ZHONG Z H.The application of SST turbulence model in the aerodynamic simulation of the automobile[J].Automotive Engineering,2003,25(4):326-329.(in Chinese)
吴军,谷正气,钟志华.SST湍流模型在汽车绕流仿真中的应用[J].汽车工程,2003,25(4):326-329.
[2]MENTER F R.Two-equation eddy-viscosity models for engineering applications[J].AIAA Journal,1994,32:1598-1605.
[3]KLEB W.Computational aeroheating predictions for X-34[J].Journal of Spacecraft and Rockets,1999,36(2):179-188.
[4]SAHU J,EDGE H L,HEAVEY K R,et al.Computational fluid dynamics modeling of multi-body missile aerodynamic interference[R].U.S.Army Research Laboratory,ARL-TR-1765,Aberdeen Proving Ground,MD,1998.
[5]DESPIRITO J,PLOSTINS P.CFD prediction of M910 projectile aerodynamics:unsteady wake effect on magnus moment[R].AIAA 2007-6580.
[6]Arrow Tech Associates.PRODAS version 3 technical manual[M].South Burlington,VT,2002.
[7]DESPIRITO J,HEAVEY K R.CFD computation of magnus moment and roll damping moment of a spinning projectile[R].AIAA 2004-2713,2004.
[8]ZHANG S S.Fluid dynamics and application[M].Wuhan:Huazhong University of Science and Technology Press,2011:5-10.(in Chinese)
张师帅.计算流体动力学及其应用[M].武汉:华中科技大学出版社,2011:5-10.
[9]MENTER F R.Zonal two equationk-ωturbulence models for aerodynamic flows[R].AIAA 93-2906,1993.
[10]ZHANG C C,REN L Q,WANG J.Simulation on flow control for drag reduction of revolution body using bionic dimpled surface[J].ACTA Armamentarii,2009,30(8):1066-1072.(in Chinese)
张春成,任露泉,王晶,等.旋成体仿生凹坑表面流场控制减阻仿真分析[J].兵工学报,2009,30(8):1066-1072.
[11]SUN Z W,CHENG Z Y,BAI J Q.A high efficient method for computing dynamic derivatives of aircraft based on quasi-steady CFD method[J].Flight Dynamics,2010,28(2):28-30.(in Chinese)
孙智伟,程泽荫,白俊强,等.基于准定常的飞行器动导数的高效计算方法[J].飞行力学,2010,28(2):28-30.
[12]DENG F.Investigations of grid fins aerodynamic shape design and the roll characteristics of wing-body configuration[D].[Ph D.Dissertation].Nanjing:Nanjing University of Science&Technology,2011.(in Chinese)
邓帆.栅格翼气动外形设计及其翼身组合体滚转特性的研究[D].[博士学位论文].南京:南京理工大学,2011.
[13]DESPIRITO J,PLOSTINS P.CFD Prediction of M910 projectile aerodynamics:unsteady wake effect on magnus moment[R].AIAA 2007-6580,2007.
[14]XU A Y.Study of two-dimension trajectory correction projectile aerodynamic characteristic[D].[Master Thesis].Nanjing:Nanjing University of Science&Technology,2010.(in Chinese)
许安勇.二维弹道修正弹的气动特性研究[D].[硕士学位论文].南京:南京理工大学,2010.
[15]XU M Y.Rocket exterior ballistics[M].Defense Industry Press,1980:224-226.(in Chinese)
徐明友.火箭外弹道学[M].国防工业出版社,1980:224-226.
Numerical simulation of a spinning stabilized projectile aerodynamic characteristics effected by structure errors
CHEN Dongyang,LAITH K.Abbas,RUI Xiaoting,WANG Guoping
(Institute of Lunch Dynamics,Nanjing University of Science&Technology,Nanjing 210094,China)
Based on the(Shear Stress Transport)SSTk-ωturbulent model,the effets of vehicle′s model with structure errors are investigated using computational fluid dynamic(CFD)method.Firstly,the aerodynamic coefficients of the model without structure errors are calculated in the conditions of different Mach numbers and spinning speeds,and the results are compared with that of the experimental data.CFD calculations predicted the drag,normal force,pitching moment,and normal force center of pressure very well,and their errors are within 10% of the experimental data which verified the accuracy and feasibility of the CFD output.Then,the models without structure errors and the models with structure errors including projectile′s mass asymmetry and coaxial error are established,and their aerodynamic characteristics are numerically calculated by CFD.The results shown that the model of mass asymmetry have a great influence on its roll damping coefficient and magnus moment coefficient derivative,and the model with coaxial error have a great influence on its normal force coefficient derivative,pitching moment coefficient derivative,magnus moment coefficient derivative and center of pressure location.Projectiles′aerodynamic characteristics coefficients may have a prodigious change due to structure errors,and the flight stability of the model may be effected by these coefficients′prodigious change.The flight trajectory and stability also will be affected accordingly.
structure errors;turbulent model;CFD;spinning
V448.15+3
Adoi:10.7638/kqdlxxb-2013.0059
0258-1825(2014)05-0705-07
2013-05-31;
2013-08-07
新世纪优秀人才支持计划资助(NCET-10-0075)
陈东阳(1988-)男,汉族,江苏连云港人,硕士研究生,研究方向为流固耦合,气动热弹性仿真.E-mail:cdy_1988@sina.cn
Laith K.Abbas(1965-),男,伊拉克人,教授,博导,研究方向为气动弹性、结构力学、多体系统动力学.E-mail:laithabbas@yahoo.com
陈东阳,Laith K.Abbas,芮筱亭,等.结构误差对旋转稳定弹丸气动特性影响的数值模拟[J].空气动力学学报,2014,32(5):705-711.
10.7638/kqdlxxb-2013.0059. CHEN D Y,Laith K Abbas,RUI X T,et al.Numerical simulation of a spinning stabilized projectile aerodynamic characteristics effected by structure errors[J].ACTA Aerodynamica Sinica,2014,32(5):705-711.
