结冰表面粗糙度预测与分析

常士楠，王 超，赵媛媛，李 延

（北京航空航天大学 航空科学与工程学院，北京 100191）

结冰表面粗糙度预测与分析

常士楠，王 超，赵媛媛，李 延

（北京航空航天大学 航空科学与工程学院，北京 100191）

通过对结冰表面液态水的受力分析，确定了水膜、水珠和细流特征粗糙度的大小及其之间的界限划分，发展和完善了结冰表面的粗糙度模型，开发了耦合该粗糙度模型的多步结冰计算程序；利用该程序计算结冰表面的粗糙度大小和分布特征，并对粗糙度影响下的流动和换热特性进行了计算分析；研究发现，结冰表面的粗糙度在分布是不均匀的，且随着结冰温度的降低，局部粗糙度的最大值降低，但在整个结冰过程中，局部粗糙度的最大值表现出增加的趋势；粗糙度的存在增强了结冰表面的对流换热。

粗糙度；水膜；水珠；细流；结冰

0 引 言

当飞机遭遇含有过冷水滴的结冰云层时，会发生结冰现象。飞机结冰过程是一个复杂的气-液-固三相流动换热问题，结冰表面的表面特性如粗糙度等对飞机结冰表面气流流动、传热与传质、表面撞击水形态等产生影响，并最终对结冰的生长方式和结冰类型产生重要影响，从而影响因结冰而导致的气动性能恶化甚至飞行安全。目前关于飞机结冰的研究大多主要基于Messinger在1953年提出的结冰传热模型［1］。该模型揭示了结冰表面的各项主要传热热流。在给定流场分布和水滴撞击特性的情况下，利用该模型所建立的能量平衡方程，再结合结冰过程中伴随的质量平衡方程，就能够进行飞机表面的结冰模拟和预测。然而这种模拟方法几乎没有考虑结冰表面的物理特性对结冰的影响，获得的结果往往与相同条件下的试验结果吻合度不够理想，很难反映真实的飞机结冰情况。九十年代初期，Shin等针对结冰表面的特性发展了等效粗糙度模型（Shin model）［2］，该模型将结冰表面粗糙度高度ks表达成结冰条件的简单函数，其计算表达式为：

其中LWC为液态水含量，g／m3；T∞为环境温度，K；u∞为飞行速度，m／s；c为翼型的弦长，m。国内外的研究人员大多采用该粗糙度模型开展结冰模拟。易贤将等效粗糙度模型耦合到结冰程序中开展了二维和三维结冰预测［3］；杨秋明等将等效粗糙度模型和动网格原理结合，对不同条件下的结冰展开多步结冰模拟，并取得了和实验结果一定程度的近似［4］。陈维建等在流场计算的湍流模型壁面函数中加入了粗糙度的影响［5］，但文中关于粗糙度对流动的影响并非针对飞机结冰的特殊情况（飞机结冰表面的雷诺数远大于普通流动）。需要指出的是，在给定的结冰计算条件下等效粗糙度模型的粗糙度高度为一定值，亦即假定机翼整个结冰表面都具有同样的粗糙高度，这种假定显然与实际情况有所区别。

20世纪80-90年代，Olsen和Hansman利用微摄影和图像处理技术对结冰表面的粗糙度形态做了大量的研究［6-7］，发现了结冰表面三种粗糙度的存在形式：水膜、水珠和细流，并分析了其形成机理；Bragg等研究了粗糙度表面上的边界层发展，研究结果表明大的粗糙度高度导致了翼型表面边界层由层流到紊流的转变过程比在光滑或小粗糙度翼型表面大大提前［8］；Fortin等建立了粗糙度分析模型，并利用该模型进行了二维结冰预测［9］。

尽管基于表面特性的飞机结冰机理研究已逐渐引起研究人员的重视，但由于影响结冰的因素非常之多，相互之间又有错综复杂的非线性关系等，仍然存在许多难点有待突破，如结冰表面特性（如粗糙度尺度、位置和分布等）的形成规律、与结冰条件的关联性等研究少有报道。

本文在总结以往研究的基础上，对结冰表面的粗糙度的形成特点及相关参数进行了分析确定，并依据结冰表面液态水的受力特性对表征粗糙度特征的水膜、水珠和细流之间的分界进行了推导界定，进一步发展了结冰表面的局部粗糙度模型，并在该粗糙度模型的基础上研究了结冰过程中局部粗糙度的大小和分布以及粗糙度影响下的换热特性，为深入有效的探究飞机结冰的机理提供理论依据。

1 局部粗糙度模型的建立

以水膜、水珠和细流为特征的粗糙度大小的确定是通过对壁面上微元控制体进行传热、传质分析以及液态水的受力分析得到的。

1.1 水膜区粗糙度

水膜表面并非光滑平整，而是存在一定程度的波动，这种波动程度的大小即为水膜区粗糙度值。取结冰表面一水膜控制体为研究对象，如图1所示，其受到的气动剪切力τi表示为：

式中：μw为水膜的动力粘度，Pa·s；u为速度，m／s；y为液膜的厚度变量，m。式（1）在初始条件y＝0，u＝0下，可得到液膜速度的关系式为：

则水膜中的平均流速¯u和水膜的质量mw可分别为：

式中ρw为水膜的密度，g／m3；Δb和ef，o分别为液膜控制体的宽度和水膜厚度，m。如图1所示，对于二维问题，可取Δb＝1。

具体到结冰过程而言，控制体内的液态水的质量

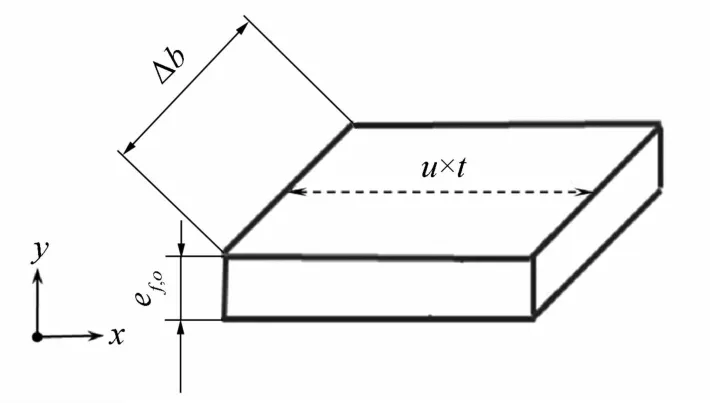
图1 水膜控制体示意图Fig.1 Sketch of the film control volume

可由下式求得：

式中f为冻结系数，mcap和mevap分别为撞击到控制体内的液态水量和蒸发量，kg／s；min为从上一个控制体溢流进的液态水质量，kg／s。

容易得到水膜的厚度为：

根据水膜区粗糙度大小的实验结果，引入一个校准因子f对水膜厚度进行修正［9］，修正后的水膜厚度为：

式中f＝15，液膜表面的粗糙度可以表示为：

g为重力加速度，m／s2。

由上述各表达式的参数可看出，水膜区粗糙度的大小主要取决于水膜受到的剪切力和本身的特性，如水的粘性、密度等，其中对于剪切力τi将在1．3节给出具体求解过程。

1.2 水珠和细流区粗糙度

水珠在结冰表面受到的作用力有气动力Fd、表面张力Fσ、壁面支持力Fz和重力Fg，如图2所示。沿气流方向，水珠在重力切向分量、气动力、表面张力三者作用下保持稳定状态，当上述力的平衡遭到破坏时，水珠会在气流的吹袭作用下向后移动，水珠在移动前能够达到的最大高度eb视为水珠状粗糙度，其值大小可根据水珠的受力平衡进行求解。

图2 水珠受力示意图Fig.2 Mechanical analysis of the bead on the icing surface

忽略水珠所受到的气动升力，即认为水珠不会从结冰表面脱落。此时，水珠受到的气动力可表示为：

式中ρa为空气的密度，kg／m3；ue为边界层外边界速度，m／s；把水珠等效成一球形颗粒，阻力系数Cd取值为0．44；Ab为水珠的迎风面积，m2，求解式为：

式中：eb为水珠高度，m；θc为水珠未变形时的接触角度，rad。

水珠的表面张力可以由下面的积分关系式求得：

σ为水珠的表面张力，N／m；r为水珠底面圆半径，m；表示为：

式中θ和φ分别为水珠与结冰表面的接触角和表面倾斜角度，rad，如图2所示。在外力作用下水珠与结冰表面的接触角θ不断变化，其变化关系可认为服从简单的余弦分布［9］，可表示为：

式中Δθc表示水珠与壁面接触的滞后角度，rad。

以上各式中涉及到的接触角θc和滞后角Δθc以及表面张力系数σ三个参数的取值大小会直接影响水珠区粗糙度的计算精度。本文依据文献［7］和文献［10］的试验结果，如图3所示，采用数值拟合的方法确定各个参数的表达式如下：

图3 相关参数的拟合Fig.3 Fitting the relevant parameters

上式中te为边界层温度，℃。

重力沿结冰表面切线方向的分量为：

式中V为水珠体积，求解表达式为：

综合式（10）、式（12）和式（18）可得水珠受力平衡关系式为：

从以上对于水珠所受的各项力的分析可以看出，获得结冰表面边界层的速度和温度分布后，即可以通过求解式（20）得到水珠高度eb，对于边界层的求解见本文第2部分。

假定水珠区粗糙度值和细流区粗糙度值相同，大小都为水珠的高度，即：

1.3 粗糙度区的分界

根据实验观测的结果，水膜位于结冰表面的最前缘，水珠位于水膜和撞击极限之间，细流位于撞击区域之外［7］。当结冰条件改变时，三种形态的分布范围也会随之变化。确定不同形态粗糙度之间的分界对于准确预测结冰表面的粗糙度大小具有重要意义。本文通过液膜表面的受力分析对其分界进行确定。

a）水膜与水珠的分界

水膜在沿结冰表面流动的过程中，受到空气的剪切应力作用，同时，水膜与结冰表面之间存在着由表面张力引起的内聚力，当剪切应力大于内聚力时，水膜能够保持形态不变而继续向前流动，而当剪切应力与内聚力平衡或者小于内聚力时，水膜则会在表面张力的作用下聚集成水珠。因此，水膜与水珠（细流）的分界可通过对结冰表面液态水进行受力分析得到。

水膜所受的剪切应力的求解表达式为［11］：

式中，u∞为远场来流速度，m／s；Ai为水膜表面积，m2；Cf为摩擦系数，其数值可以通过经验公式得到［12］：

ks表示距离前缘弧长为s处的局部粗糙度，m；称ks／s为无量纲粗糙度。

由表面张力引起的水膜内聚力的计算公式为：

式中，τσ水膜内聚力，N；Sσ为水膜周长，m。对于二维问题，微元控制体宽度假定为1，当τi≥τσ时，可得：

令Cf，c为临界摩擦系数，表示为：

即当Cf≥Cf，c时，粗糙度保持水膜状态；反之，当Cf＜Cf，c时，水膜聚集成水珠。

b）水珠与细流的分界

若水膜在撞击极限前转变为水珠，并且在撞击极限外仍有溢流情况发生，此时，液态水会以细流形态存在。因此，可认为水珠与细流的分界就是水滴撞击极限。

2 耦合了粗糙度的换热模型及算法

结冰翼型壁面的流动非常复杂，流动存在一个从层流到湍流变化的复杂过程，转捩点位置的判定对流动类型的区分十分重要。为此，引入粗糙度雷诺数的概念［13］。定义

式中，Rek为粗糙度雷诺数，ν为空气的运动粘度，m2／s；uk为对应粗糙度y＝ks处的空气速度，m／s，可采用型线假设法求解［14］：

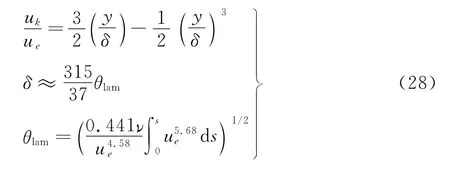
式中δ为边界层厚度，m；θlam为层流区动量边界层厚度，m。

当Rek≤600认为流动为层流，层流区域中的对流换热系数表示成无量纲Stanton数为：

式中普朗特数Pr表达式为：

式中Cpa为空气的比热容，J／（kg·K）；λ为空气的导热系数，W／（m·K），是边界层温度te的函数：

当Rek＞600认为流动为湍流，流动区域中的对流换热系数表示成无量纲Stanton数为：

式中，Pri为湍流普朗特数，取值为0.9；Stk为粗糙度Stanton数，表达式为：

由式（32）和式（33）即可求得湍流区域的换热系数。

由于粗糙度的微观尺度原因，对粗糙度模型的预测精度提出了较高的要求。为了有效的对所建立的局部粗糙度模型进行评估，实现对结冰表面粗糙度大小和分布特点及粗糙度影响下的换热特性的精确预测，开发了耦合局部粗糙度模型的多步结冰预测程序，算法流程如图4所示。

图4 计算流程图Fig.4 Flow chart of computation

3 算例分析

选取NACA0012翼型为计算模型，并以结冰时间为360s时的计算结果分别从结冰表面平均粗糙度和冰形两方面与文献数据进行对比分析，其中，流场计算部分借助Fluent计算流体软件［15］完成，结冰模型采用经典的Messinger热质耦合模型［1］。计算条件列于表1中。

表1 计算条件Table 1 Calculation conditions

3.1 平均粗糙度预测

针对局部粗糙分析模型，引入平均沙粒粗糙度的概念，即对结冰表面上所有微元控制体内的粗糙度进行积分，求出积分平均值，该值即为等效沙粒粗糙高度，表示为式（34）。选取的计算温度为-4．4℃，-6．1℃，-7．8℃，-10℃，-13．35℃，-19．4℃，-28．4℃。

式中ds为微元控制体弧段长度，m。

图5给出了各温度条件下，采用局部粗糙度模型所得的平均粗糙度值与Shin等效粗糙度模型和Fortin模型的对比结果。本文开始部分已经对等效粗糙度模型进行了说明，由式（1）也可以看出，在给定结冰条件下，由该模型计算得到的粗糙高度与温度呈线性关系。文中的预测结果与Fortin模型的预测值较为接近。局部粗糙度模型是基于壁面微元控制体内的热质平衡和对液态水的受力分析建立起来的模型，综合考虑了环境温度、气流速度、液态水含量（LWC）等结冰条件以及液态水与固体壁面的接触角度、长度和面积等多种几何因素的影响，因此，导致了采用局部粗糙度模型得到平均粗糙度值具有较高程度的非线性分布。

图5 不同温度时平均粗糙度大小对比Fig.5 Comparison of average roughness at different temperature

3.2 冰形预测

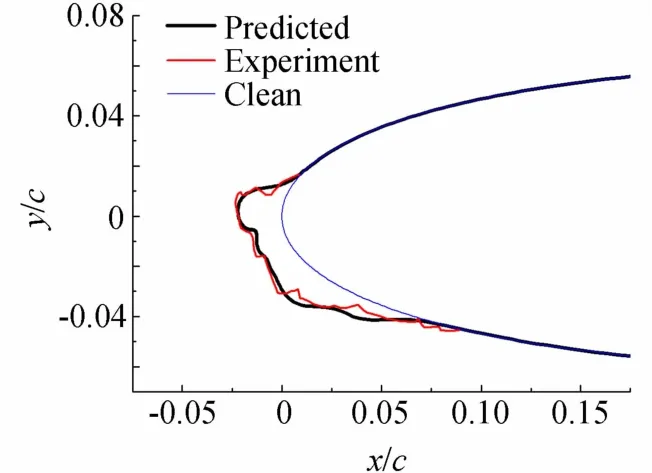
图6 混合冰结冰条件下的冰形比较Fig.6 Comparison of ice shapes under the mixedicing condition

冰形是耦合了局部粗糙度模型的多步结冰程序的最终计算结果，是考量模型算法的重要标准。从图6中可以看出，本文的计算程序对于形状复杂的混合冰的冰角位置、结冰冰形以及结冰量等预测结果与实验结果吻合较好，表明文中耦合了局部粗糙度模型的算法程序用于过冷水滴的撞击结冰是成功的。

4 耦合局部粗糙度模型的计算结果与分析

通过对局部粗糙度模型的分析可知，水膜状、水珠状以及细流状粗糙度的分布特征是结冰气象条件和流体力学因素共同作用的结果，因此，探究不同条件下的结冰表面的粗糙度分布范围和大小，对于从微观角度揭示飞机结冰机理具有重要意义。

4.1 结冰过程中局部粗糙度大小与分布

图7 不同温度条件下结冰表面的局部粗糙度分布Fig.7 Local roughness distribution on the icing surface for different temperatures

图7给出了结冰过程中结冰表面局部粗糙度大小和分布特点。结冰过程中，由于结冰表面液态水形态的变化，促使冰层的不断累积，从而造成结冰表面流场的不断变化，而流场的变化又会影响结冰表面液态水的量与分布，从而引起局部粗糙度的大小和分布变化。容易看出，利用本文程序预测的粗糙度在结冰表面上呈“M”形分布，驻点处的粗糙度值在整个结冰过程中都是最小的；沿弦长气流运动方向，粗糙度值逐渐增大，并在一定位置处达到最大值；在结冰过程中，粗糙度的最大值表现出增加的趋势，但是综合三种温度条件下的粗糙度分布而言，粗糙度的最大值（-4．4℃，ks，max＝2．72mm；-6．1℃，ks，max＝2．45mm；-10℃，ks，max＝1．6mm）是随着环境温度的降低而降低的，这是因为温度的降低促使结冰表面的液态水量的减少，从而使局部粗糙度变小。

4.2 结冰表面对流换热特性分析

图8 结冰过程中结冰表面的Rek分布Fig.8 Distribution of Rekon the surface during the icing process

结冰表面气流的流动形态对表面的对流换热起着重要作用，其中层流区与湍流区的分布和范围大小反应了结冰表面的对流换热特性。图8给出了不同环境温度条件下结冰表面的粗糙度雷诺数分布的计算结果。粗糙度雷诺数Rek为600的水平线把Rek分布曲线与横向坐标轴围成的区域分成了上下两部分，水平线上方区段对应的弧长范围表示结冰表面的湍流区域，水平线下方区段对应的弧长范围表示结冰表面的层流区域。从图中可以看出，特定温度下的结冰过程中，结冰表面的流动形态的区域和大小几乎没有发生变化；随着温度的降低（-4．4℃，-6．1℃，-10℃），结冰表面的湍流区域范围减小，且表征流动形态的粗糙度雷诺数的最大值也减小。对比图7可以看出，湍流区对应着粗糙度值较大的分布区域。

结冰表面流动区域内的对流换热系数大小可用无量纲对流换热系数Stanton数（St）来表示。当流动为层流时，St与粗糙度的关系如图9（a）所示，St随着无量纲粗糙度ks／s的增加而增加，因此，当同一弧长位置处的粗糙度增加时，St增加，即结冰表面的对流换热作用增强；当流动为湍流形态时，St主要受粗糙度、粗糙度Stanton数（Stk）的影响，其影响关系如图9（b）所示。无量纲粗糙度ks／s对St的影响作用与流动为层流时相同；当ks／s不变时，St随着Stk的增加表现出增加的趋势，但是当Stk＞10时，St不再随Stk的增加而发生变化，即此时可以忽略粗糙度Stanton数Stk对结冰表面的对流换热作用的影响。

从以上的分析可知，相同的条件下结冰表面的粗糙度越大，其表面的对流换热作用越强。

图9 无量纲粗糙度ks／s对St的影响Fig.9 Effect of ks／s on St

5 结 论

本文在对结冰表面液态水的受力分析的基础上发展了局部粗糙度模型，开发了耦合局部粗糙度模型的多步结冰程序，并对结冰表面的粗糙度分布特性和粗糙度影响下的结冰表面的传热特性进行了研究，得出以下主要结论：

（1）局部粗糙度模型在一定程度上反映了结冰表面粗糙度的分布特点。利用耦合了该粗糙度模型的多步结冰程序对结冰表面粗糙度和结冰冰形进行了模拟计算，计算结果有助于从微观角度认识过冷水滴的撞击结冰机理。

（2）结冰表面的局部粗糙度的分布是不均匀的，但在整个结冰过程中粗糙度的整体分布是稳定的；在本文的计算条件下，粗糙度较大的区域气流流动的形态由层流转变为湍流，粗糙度促进了流动区域内的对流换热。

（3）局部粗糙度模型综合考虑了结冰表面不同区域粗糙度的大小和形态，与实际的结冰表面比较近似，在今后的结冰代码的改进与开发中应着重考虑局部粗糙度模型。

［1］MESSINGER B L．Equilibrium temperature of an unheated icing surface as a function of airspeed［J］．Journal of the Aeronautical Sciences，1953，20（1）：29-42．doi：10．2514／8．2520

［2］JAIWON Shin，BRIAN Berkowitz，HSUN Chen，et al．Prediction of ice shapes and their effect on airfoil performance［R］．AIAA 91-0264．

［3］YI X．Numerical computation of aircraft icing and study on icing test scaling law［D］．［PHD Thesis］．China Aerodynamics Research and Development Center，2007．（in Chinese）

易贤．飞机积冰的数值计算与积冰试验相似准则研究［D］．［博士学位论文］．绵阳：中国空气动力研究与发展中心，2007．

［4］CHANG S N，YANG Q M，LI Y．Quasi-steady numerical simulation of ice accretion on airfoil［J］．ACTA Aerodynamica Sinica，2011，29（06）：302-308．（in Chinese）

常士楠，杨秋明，李延．翼型表面结冰准定常数值模拟［J］．空气动力学学报，2011，29（06）：302-308．

［5］CHEN W J，ZHANG D L．Numerical simulation of glaze ice accretion process［J］．Journal of Aerospace Power，2005，20（3）：472-476．（in Chinese）

陈维建，张大林．瘤状冰结冰过程的数值模拟［J］．航空动力学报，2005，20（3）：472-476．

［6］OLSEN W，WALKER E．Experimental evidence for modifying the current physical model for ice accretion on aircraft surfaces［R］．NASA TM-87184，1986．

［7］HANSMAN R J Jr，REEHORST A，SIMS J．Analysis of surface roughness generation in aircraft ice accretion［R］．AIAA 92-0298．

［8］BRAGG M B，CUMMINGS M J，HENZE C M．Boundary-layer and heat-transfer measurements on an airfoil with simulated ice roughness［R］．AIAA 96-0866．

［9］GUY F．Prediction of 2D airfoil ice accretion by bisection method and by rivulets and beads modeling［R］．AIAA 2003-1076．

［10］LUXFORD G．Experimental and modelling investigation of the deformation，drag and break-up of drizzle droplets subjected to strong aerodynamics forces in relation to SLD aircraft icing［D］．Cranfield university school of engineering，2005．

［11］TOMPSON B E，MARROCHELLO M R．Rivulet formation in surface-water flow on an airfoil in rain［J］．AIAA Journal，1999，37（1）：45-49．

［12］BEAUGENDRE H，MORENCY F，HABASHI W G．Roughness implementation in fensap-ice：model calibration and influence on ice shapes［J］．Journal of Aircraft，2003，40（6）：1212-1215．doi：10．2514／2．7214

［13］Von DONEHOFF A，HORTON E．A low-speed experimental investigation of the effect of a sandpaper type of roughness on boundary-layer transition［R］．NACA Report No．1349，1956．

［14］ZHANG Z X，DONG Z N．Viscous fluid mechanics［M］．Beijing：Tsinghua University Press，1999．（in Chinese）

章梓雄，董曾南．粘性流体力学［M］．北京：清华大学出版社，1999．

［15］FLUENT 6．3 User′s Guide［M］．2006．

Modeling of roughness dimension and distribution on the icing surface

CHANG Shinan，WANG Chao，ZHAO Yuanyuan，LI Yan
（School of Aeronautic Science and Engineering，Beihang University，Beijing 100191，China）

It′s recognized that the roughness dimension and distribution on the icing surface influence the flow structure in the boundary layer and thus the heat transfer characteristics is affected further．Therefore，constructing an appropriate roughness model becomes a strong requirement in order to predict the ice shape accurately．In the current work，a local roughness model was developed based on the mechanical analysis of the liquid water on the icing surface．The proposed roughness model is characterized by film，beads and rivulet．The boundaries between film，beads and rivulet are defined according to the experimental observations in references．The set of transient governing equations developed were solved numerically with the finite vol-ume method using a computational fluid dynamics（CFD）code．The mathematical model can be used to analyze the effect of different icing conditions on the roughness and thus the characteristics of the heat transfer in the icing process can be obtained．Numerical results are presented to show the applicability of the developed model and can be helpful to understand the icing mechanism further．In addition，the multi-step ice predicting code developed in this work can be applied in anti／deicing system design directly．The predictions show that the roughness distribution on icing surface is non-uniform，and the maximum roughness is decreasing with temperature decreases．However，during the whole icing process，the maximum roughness performs an increasing trend．The convective heat transfer was enhanced due to the roughness on icing surface．

roughness；film；beads；rivulet；ice accretion

O359

Adoi:10.7638／kqdlxxb-2012.0177

0258-1825（2014）05-0660-08

2012-10-30；

2013-01-01

国家自然科学基金（10872020，11072019，11372026）

常士楠（1968-），教授，研究方向：飞机和发动机结冰及防／除冰研究．E-mail：sn＿chang＠buaa．edu．cn

常士楠，王 超，赵媛媛，等．结冰表面粗糙度预测与分析［J］．空气动力学学报，2014，32（5）：660-667．

10．7638／kqdlxxb-2012．0177． CHANG S N，WANG C，ZHAO Y Y，et al．Modeling of roughness dimension and distribution on the icing surface［J］．ACTA Aerodynamica Sinica，2014，32（5）：660-667．