多区域自由变形技术在短舱安装位置减阻设计中的应用研究

白俊强，徐家宽，黄江涛，乔 磊

（1．西北工业大学 航空学院，陕西 西安 710072；2．中国空气动力研究与发展中心，四川绵阳 621000）

多区域自由变形技术在短舱安装位置减阻设计中的应用研究

白俊强1，徐家宽1，黄江涛2，乔 磊1

（1．西北工业大学 航空学院，陕西 西安 710072；2．中国空气动力研究与发展中心，四川绵阳 621000）

为了进行短舱安装位置参数的减阻优化设计研究，首先在NURBS样条基函数的基础上建立了多区域自由变形（FFD）技术，通过对FFD控制体框架边界条件的合理选取建立组合框架，实现了多个控制框架对复杂外形不同区域的自由变形参数化，采用多个控制框架的空间控制体对某型客机短舱安装位置进行减阻优化设计。试验设计取样之后应用随机权重粒子群算法和Kriging代理模型建立气动外形优化系统，对某型客机短舱水平位置和水平安装角进行气动优化设计。优化设计结果表明，设计后的短舱位置使得整个飞机在一定攻角范围内的阻力显著减小，从而证明了基于多区域自由变形技术建立的优化设计系统是合理和实用的。

短舱减阻；多区域FFD技术；组合框架；粒子群算法；Kriging代理模型

0 引 言

针对大型运输机及客机，发动机短舱的气动设计要求短舱外部阻力要尽可能的小，在短舱几何外形确定的情况下，发动机短舱安装位置对于短舱减阻则起着至关重要的作用。在高速巡航状态下飞机的发动机短舱安装位置优化，减小整个飞机阻力，对于节约油耗和飞机运行成本具备重要意义。

在发动机短舱安装位置优化设计中，短舱与机身的相对位置及短舱轴线与机身基准线之间的水平扭转角为发动机短舱安装位置优化的两个重要设计参数。短舱挂架的组合设计要求干扰阻力小，而短舱在挂架上的安装位置对干扰阻力影响很大。因此，在进行短舱安装参数的确定时，需要对其进行优化设计，从而获得更小的干扰阻力。

而如果使用传统的建模-网格生成策略，不断地试验短舱安装参数则会带来极大的工作量，导致设计周期急剧增长。所以，需要使用优化设计方法对短舱安装位置进行优化设计。而优化设计的首要问题就是参数化建模，参数化建模方法的优劣直接决定了其对几何外形的描述能力。本文使用FFD（Free-Form-Deformation）自由变形技术对优化设计对象进行参数化建模，其对于几何外形的描述精度非常高，关于该方法，国内朱心雄［1］和黄江涛［2］等人以及国外Andreoli［3］和Sederberg［4］等人都进行了大量的研究。而本文根据优化设计问题的复杂性，基于他们的研究工作，发展了多区域FFD技术，实现了多个控制框架对复杂外形不同区域的自由变形参数化设计。对短舱，挂架和机身采用不同的控制框架，从而实现多个设计对象的参数化和不同设计对象间的光滑过渡，从而实现短舱安装参数的优化设计。应用Delaunay图映射技术进行空间网格变形，取样进行CFD计算后利用Kriging代理模型对CFD计算结果数值拟合预测，结合随机权重粒子群算法构建了短舱安装位置优化设计系统，对某型客机发动机短舱在挂架上的安装位置进行了参数优化设计研究。优化设计结果表明，设计后的短舱位置使得整个飞机在一定攻角范围内的阻力显著减小，验证了本文多区域自由变形技术的可行性和合理性。

1 多区域FFD自由变形参数化方法和Delaunay图映射变形网格技术

本文建立了多区域FFD自由变形技术，FFD方法［1-4］由三个步骤构成：第一步，将待变形的实体嵌入建立的FFD控制框架中，确定待变形物体上任意点（x，y，z）所对应的局部坐标（u，v，w），对于一般情况，该问题需要求解非线性方程组；第二步，对参数实体施加变形，这个过程通常由移动三维框架的控制顶点来实现；第三步，计算框架变形对嵌入物体的影响，此时通过第一步所得物体上的点的局部坐标和第二步中变形后的控制框架来计算变形后物体上相应点的新位置。自由变形在数学上可以看作是R3到R3的映射X＝F（x），输入为待变形物体表面所包围的实体，输出为变形后的物体。对于复杂构型的物体进行局部变形时，需要更合理的FFD的空间拓扑，为此本文应用非均匀有理B样条基函数进行任意物理空间属性构建，可以保持变形物体任意阶的导矢连续性，整体局部均可使用，实现多区域FFD空间变形技术对复杂外形的局部变形。

建立多个FFD控制框时，需要考虑不同框架之间曲面的连续性问题，若两个FFD变形X1ffd（s1，i1，u1），X2ffd（s2，i2，u2）有共同边界s0＝s1＝0，则变形后的曲面沿v和w方向的一阶导矢如下：

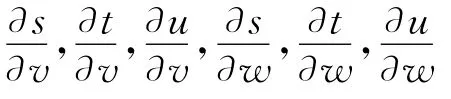
从上式中看出与曲面变形无关，满足多FFD空间跨界导矢连续的条件为：

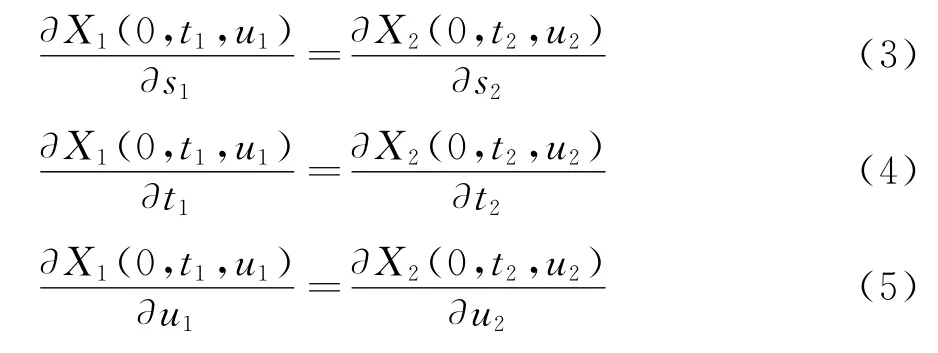
而在FFD方法第二步计算局部坐标过程中求解高阶非线性方程组，其逻辑坐标为一组复变量，很难求出精确解析函数，因此对参数空间坐标的逆映射转换为对该空间复变量问题的参数辨识，从而建立如下数学模型：

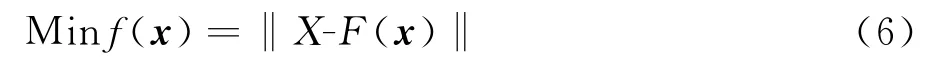
本文所采用参数辨识方法为粒子群寻找上述数学模型最优值和牛顿-拉夫逊法，其基本思想：首先用粒子群搜索得到的全局最优解达到小于1×10-3的精度，将此参数作为初始值，再用梯度法，修正∇2f（x），构造一个对称正定矩阵Gk，用Gk取代∇2f（x），从而得到方程：Gkdk＝－∇f（xk），解此方程，得到点xk处的下降方向：dk＝－G－1∇f（xk），就能快速求解出任意物理空间点对应的参数空间坐标。

对于原控制体中任一点X所对应的局部坐标LQ（s，i，u），通过逆映射关系即可得到该点在框架变形后所对应的笛卡尔坐标：

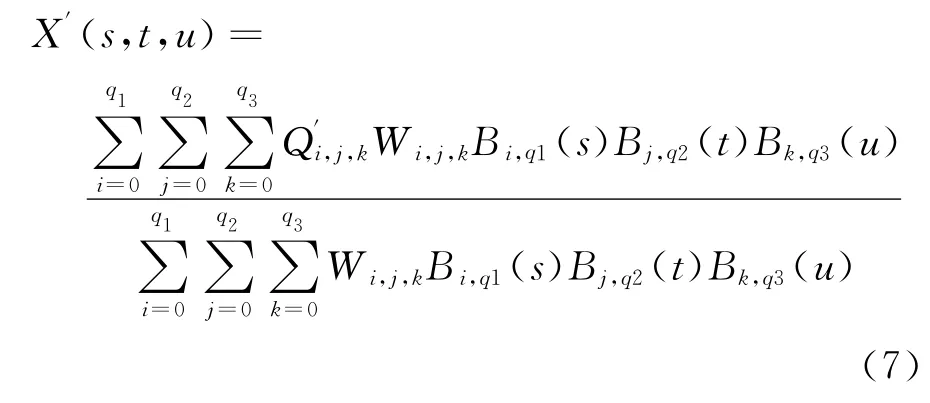
发动机短舱的FFD控制体框架如图1和图2所示，图3和图4为短舱随安装位置参数变化的变形示意图，可以看出变形后发动机短舱仍保持与挂架合理对接。

本文采用合理的FFD边界条件实现了多区域自由变形，FFD控制框由4个框架组合而成，其中框架1控制短舱，框架2-4控制挂架，框架2控制与短舱连接部分的挂架，与框架1对接。控制框1内物体表面网格的逻辑坐标分布如图6所示，与之衔接的控制框2内物体表面网格的逻辑坐标分布如图7所示。

图1 短舱挂架与FFD控制体Fig.1 Nacelle and pylon with FFD control frame

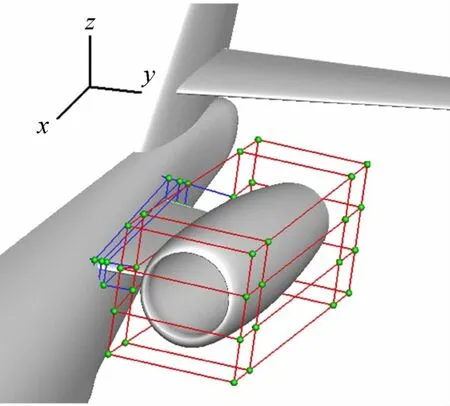
图2 全机构型与FFD控制体Fig.2 Entire configuration with FFD control frame

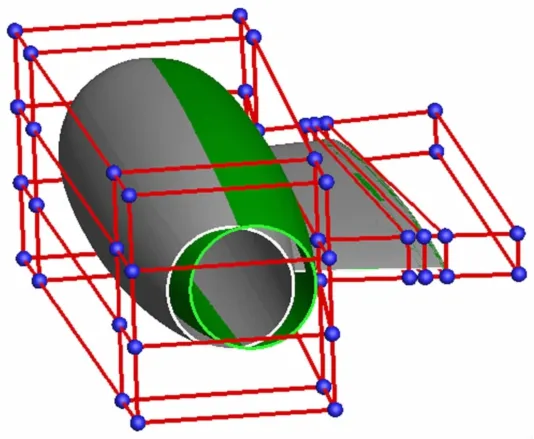
图3 短舱随安装位置变形Fig.3 Deformation of nacelle with install position

图4 全机构型短舱随安装位置变形Fig.4 Deformation of nacelle with install position in the entire configuration

图5 多区域组合FFD控制框架Fig.5 Multi-zones composite FFD frame

图6 控制体框架1内的物面网格的逻辑坐标分布Fig.6 Logic coordinates distribution of grids on the surface in FFD frame 1

图7 控制体框架2内的物面网格的逻辑坐标分布Fig.7 Logic coordinates distribution of grids on the surface in FFD frame 2

在获得自由变形后的短舱表面网格后，需要图映射变形网格技术制作新的空间网格来进行CFD计算。本文采用Delaunay图映射变形网格技术，该方法以其高效、快速、鲁棒性强等优点在动网格领域广泛应用。基于Delaunay图映射的网格变形技术基本依据为在平面或空间，给定包括流场边界点在内的一组点，即可以进行唯一的Delaunay图三角化，具体算法可参考相关文献［9-11］，从而可以完成计算区域的三角化图覆盖，进一步对空间计算域任意点进行三角网格定位，计算域网格节点定位完毕后，需建立映射关系，根据映射关系即可由不同的表面网格映射出对应的空间网格。

2 流场数值模拟方法

本文应用的控制方程是三维可压缩非定常积分形式的N-S方程。在直角坐标系下，其表达式为：

湍流模型采用Menterk-ωSST模型［12］，方程空间离散无粘项采用Roe格式，粘性项采用中心格式进行空间离散，时间推进方法采用AF近似因子分解方法，应用了多重网格及并行计算技术。边界条件包括物面边界条件、对称边界以及远场无反射边界条件［13］。通过比较DLR-F6翼身组合体带挂架短舱标模构型的计算结果和风洞试验数据，如图8所示，说明本文采用的CFD计算程序比较可靠。计算状态为：Ma∞＝0.75，Re＝3.0×106。

图8 DLR-F6翼身组合体带吊舱升阻特性Fig.8 Lift and drag properties of DLF-F6 wing-body with nacelle

3 基于随机权重粒子群算法与Kriging代理模型优化设计框架

本文优化算法采用随机权重粒子群算法［14-16］，在随机初始粒子群中，开始寻优，每一次迭代中，粒子通过跟踪粒子本身找到的最优解（即个体极值）和整个种群当前最优解（即全局最优解），更新自己的速度和位置。对于每个微粒，将其适应值与其经过的最好位置作比较，更新全局最优解，最终找到最优解和最优解的位置。其中随机权重粒子群算法的惯性因子服从某种随机分布，增强粒子群全局搜索能力，避免陷入局部最优。

高精度的代理模型是提高优化设计效率的关键，本文代理模型的构建采用Kriging代理模型［17-18］。Kriging代理模型以其在拟合高度非线性、多峰值问题中的小误差预测而广泛应用于气动优化设计中。本算例只有2个设计变量，故首先通过拉丁超立方取样（LHS），选取20个样本点进行CFD计算后获得每个样本的阻力值，然后构建Kriging代理模型即可获得非常高的函数拟合精度和预测精度，如图9为Kriging三维阻力预测值曲面及CFD计算阻力结果的对比图。图10为Kriging对阻力的预测云图。由这两幅图可知CFD计算的阻力值几乎都落在Kriging插值曲面上，即Kriging的预测精度较高。

图9 Kriging代理模型高精度预测图Fig.9 High-accuracy prediction of Kriging surrogate model

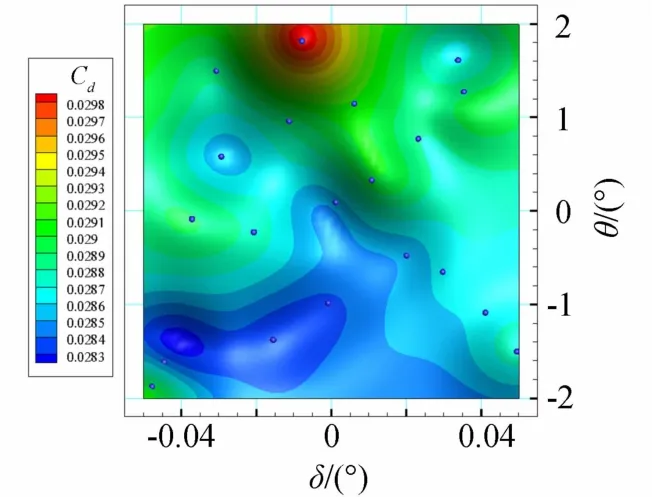
图10 Kriging阻力预测云图Fig.10 Contour of drag prediction with Kriging

4 某型客机发动机短舱安装位置参数气动优化设计

对某型民用客机发动机短舱安装位置参数进行气动优化设计，网格采用结构对接网格技术，网格单元数为1000万，表面网格如图11所示。CFD方法采用并行计算技术、Roe空间离散方法、AF近似因子分解隐式时间推进、SST湍流模型以及多重网格加速收敛技术。

图11 短舱表面网格分布Fig.11 Grid distribution of surface of nacelle

设计状态为：M∞＝0.73，Re＝1.76×107。

优化设计目标为在飞机高速巡航状态下（巡航攻角为1°），通过优化发动机短舱安装位置参数减小飞机阻力，约束条件为短舱横向移动范围在［-0．05m，0．05m］；短舱水平扭转角变化范围在［-2．0°，2．0°］。

参数化方法为多区域FFD自由变形技术，对所参数化的曲面的FFD控制体采用4个控制顶点，28个控制顶点自由变形，4个边界点控制挂接与短舱结合处，短舱在Y方向刚性移动从而改变发动机短舱距离机身的位置参数，绕控制顶点Y方向刚性旋转控制短舱轴线相对机身基准线之间的水平扭转角。优化算法为基于随机权重法的粒子群算法，群体规模为100个，每一次迭代500次以获得更加理想的解。在构建Kriging代理模型时，采用拉丁超立方方法选取样本，样本个数取为20个。对于两个设计变量来说，20个样本拟合出的Kriging代理模型的预测精度误差不到0．5%，完全符合预测要求。

通过20个样本的CFD计算结果建立Kriging代理模型，然后进行粒子群寻优。图12给出了优化前后FFD控制体框架变化示意图，短舱与机身距离减小，扭转角增大（短舱头部向机身靠近）。图13给出了发动机短舱优化前后全机在不同攻角下的升阻力计算结果，可见升力系数变化非常小，表1的结果表明优化后巡航点阻力减少4．5 Counts（1 Counts＝1×10-4），而在其他攻角飞行时阻力值减小量更大，减阻效果较为明显。

图12 FFD控制体设计前后变化Fig.12 Changes of FFD frame in the optimization design before and after

图13 优化前后阻力特性对比Fig.13 Comparison of lift and drag properties in the optimization design before and after

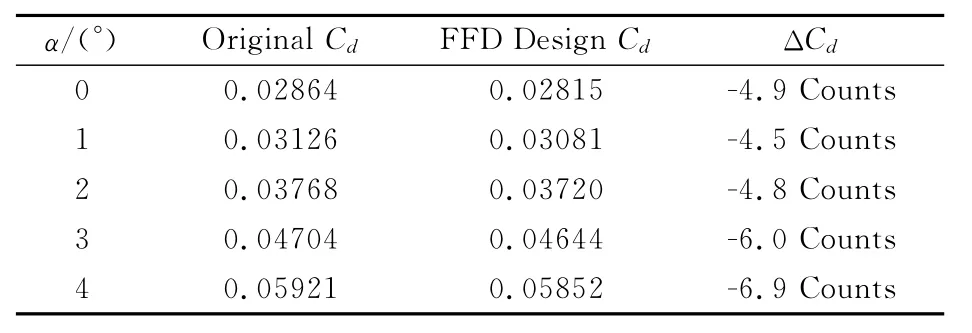
表1 优化设计前后阻力特性Table 1 Drag properties in the optimization design before and after

由图14和图15可知，优化设计后短舱唇口周围靠近挂架一侧高压区较小，短舱外侧高压区增大，发房-挂架-机身三者组成的收缩-扩张通道的干扰阻力减小，从而改善飞机的升阻力特性。图16给出了优化前后飞机在巡航状态下各部件的阻力系数的对比，由图可知挂架和短舱部分在气动优化设计之后减阻效果最为明显，约为总减阻量的54%，这说明优化安装位置后的短舱挂架部分，气流流动更为平稳，干扰阻力减小；其次是机身阻力，约为总减阻量的23%，这说明短舱与机身之间的干扰作用非常明显，优化之后机身受短舱干扰的阻力减小；其余减阻量分别来自机翼和水平尾翼，进行优化设计之后短舱使得原来机翼和水平尾翼附近的流场特性发生改变，它们之间的干扰阻力也有一定量的减小。

图14 优化前发动机进气道唇口马赫数云图Fig.14 Mach contour of air inlet lip of nacelle before optimization

图15 优化后发动机进气道唇口马赫数云图Fig.15 Mach contour of air inlet lip of nacelle after optimization

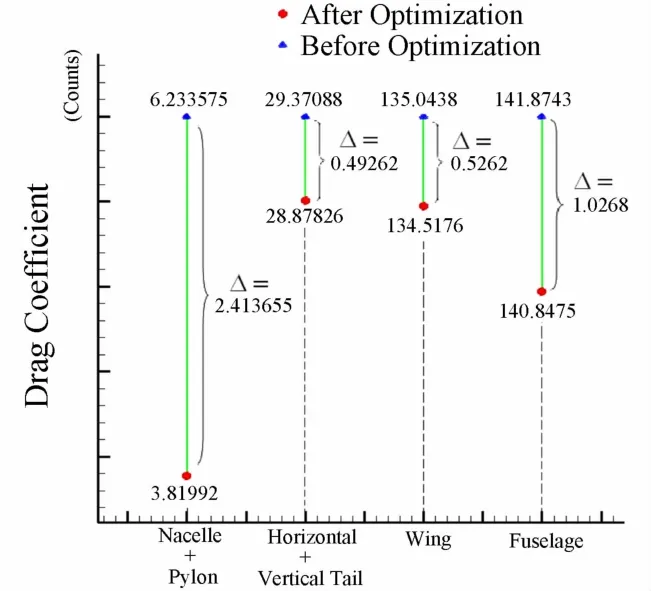
图16 优化前后飞机各部件的阻力系数Fig.16 Drag coefficient of parts of the plane in the optimization design before and after

5 结束语

本文建立了多区域FFD技术参数化方法，结合Kriging代理模型与随机权重粒子群算法构建了气动优化设计框架，采用所建立的优化设计框架，对某型客机发动机短舱进行优化设计，得到：

（1）多区域FFD技术能够很好地对发动机短舱安装位置进行参数化变形，不同区域不同变形，且连接良好。

（2）基于Kriging代理模型与粒子群算法所建立的气动优化设计框架具备较高的优化设计效率。

（3）发动机短舱经优化设计后发房-吊挂-机身三者组成的收缩-扩张通道的干扰阻力减小，巡航点飞机整体阻力下降4．5Counts。

所以，本文的多区域FFD方法有助于改善飞机气动特性和提高飞机气动优化设计效率。

［1］ZHU X X，et al．The molding technology of free curve and surface［M］．Beijing：Science Press，2000：66-112．（in Chinese）

朱心雄，等．自由曲线曲面造型技术［M］．北京：科学出版社，2000：66-112．

［2］HUANG J T，GAO Z H，BAI J Q，et al．Laminar airfoil aerodynamic optimization design based on delaunay graph mapping and FFD technique［J］．ACTA Aeronautica et Astronautica Sinica，2013，34（1）：37-45．（in Chinese）

黄江涛，高正红，白俊强，等．应用Delaunay图映射与FFD技术的层流翼型气动优化设计［J］．航空学报，2012，33（10）：1817-1826．

［3］ANDREOLI M，JANKA A，DESIDERI J A．Free-form-deformation parameterization for multilevel 3D shape optimization in aerodynamics［R］．INRIA Research Report，2003-5019．

［4］SEDERBERG T W，PARRY S R．Freeform deformation of solid geometric models［J］．Computer Graphics，1986，22（4）：151-160．

［5］BAKER T J．Unstructured meshes and surface fidelity for complex shapes［R］．AIAA 91-1591-1991．

［6］LIU X Q，QIN N．Fast dynamic grid deformation based on Delaunay graph mapping［J］．Journal of Computational Physics，2006，211（2）：405-423．

［7］MORRIS A M，ALLEN C B，RENDALL T C S．Domain-element method for aerodynamic shape optimization applied to a modern transport wing［J］．AIAA Journal，2009，7（47）．

［8］KYLE A W，KARMAN S L，BURDYSHAW C．Geometry parameterization method for multi disciplinary applications［J］．AIAA Journal，2009，6（47）．

［9］LEATHAM M，STOKES S，SHAW J A，et al．Automatic mesh generation for rapid response Navier-Stokes calculations［R］．AIAA 2000-2247．

［10］CHEW L P．Constrained Delaunay triangulations［J］．Algorithmica，1989，4（1-4）：97-108．

［11］DEVROVE L，MUCKE E，ZHU B．A note on point location of Delaunay triangulation of random points［J］．Algorithmica，1988，22（4）：477-482．

［12］MENTER F R．Two-equation eddy viscosity turbulence models for engineering applications［J］．AIAA Journal，1994，32（8）：269-289．

［13］YAN C．Computational fluid dynamics and its application［M］．Beijing：Press of Beijing University of Aeronautics and Astronautics，2006．（in Chinese）

阎超．计算流体力学方法及应用［M］．北京：北京航空航天大学出版社，2006．

［14］WANG W B．The study and application of particle swarm optimization algorithm［D］．［Ph D Thesis］．Chengdu：Southwest Jiaotong University，2012．（in Chinese）

王维博．粒子群优化算法研究及其应用［D］．［博士学位论文］．成都：西南交通大学，2012．

［15］ZHOU C，GAO H B，GAO L，et al．Algorithm of particle swarm optimization［J］．Computer Application Research，2003，（12）：7-11．（in Chinese）

周驰，高海兵，高亮，等．粒子群优化算法［J］．计算机应用研究，2003，（12）：7-11．

［17］MARTIN J D，SIMPSON T W．A study on the use of Kriging models to approximate deterministic computer models［C］．ASME 2003 Design Engineering Technical Conferences and Computers and Information in Engineering Conference，Chicago，Illinois USA，2003．

［18］MARTIN J D．Robust kriging models［R］．AIAA 2010-2854．

Drag reduction design of install position of nacelle based on multi-zone FFD technology

BAI Junqiang1，XU Jiakuan1，HUANG Jiangtao2，QIAO Lei1
（1.Aeronautics School，Northwestern Polytechnical University，Xi′an 710072，China；2.China Aerodynamics Research and Development Center，Mianyang 621000，China）

In order to conduct the drag reduction optimization design of install parameters of nacelle，multi-zone FFD technique is established based on NURBS（Non-Uniform Rational B-Spline）basis function in this paper．The composite frames are founded through choosing the boundary condition of FFD shape and lattice reasonably．Then，it can realize the FFD parameterized design of the multi-control frames for complex shape in different zones．This multi-control frame FFD technique is used to conduct drag reduction design of the install position of certain airliner nacelle．The aerodynamic optimization design system is established by combining FFD technique，random inertia weight PSO arithmetic and Kriging surrogate model．It process the aerodynamic optimization design by taking horizontal install position and horizontal torsion angle of certain airliner nacelle as design variables，and the results show that the optimized nacelle has lower drag and better aerodynamic characteristic in certain attack angle．Therefore，the optimization design system based on multi-zone FFD technique established in this paper is reasonable and practical．

nacelle drag reduction；multi-zone FFD technique；composite frames；PSO arithmetic；Kriging surrogate model

V211.3

Adoi:10.7638／kqdlxxb-2012.0185

0258-1825（2014）05-0682-06

2012-11-08；

2013-03-09

白俊强（1971-），男，河南新乡人，教授，博士生导师，主要研究方向：飞行器总体及气动设计，飞行力学，计算流体力学．E-mail：junqiang＠nwpu．edu．cn

白俊强，徐家宽，黄江涛，等．多区域自由变形技术在短舱安装位置减阻设计中的应用研究［J］．空气动力学学报，2014，32（5）：682-687．

10．7638／kqdlxxb-2012．0185． BAI J Q，XU J K，HUANG J T，et al．Drag reduction design of install position of nacelle based on multi-zone FFD technology［J］．ACTA Aerodynamica Sinica，2014，32（5）：682-687．