ABS液压系统抗冲击性能研究与仿真分析

刘小斌，尹新权，李宝栋

(兰州工业学院，甘肃兰州 730050)

0 前言

ABS(Anti-lock Braking System)防抱死制动系统其作用是当车辆在不同附着系数的路面制动时，根据车辆速度与减速度的变化，电控单元通过控制电磁阀来调节制动压力，控制车轮在理想的滑移率范围内制动，以获得最佳的制动效果和方向稳定性。然而，ABS在工作时，常伴有尖锐的噪声及振动，如何在不影响ABS作用效果的情况下平稳工作，值得研究与分析［1］。

1 ABS系统振动机制

单轮ABS系统如图1所示。当踩下制动踏板1，制动液由主缸2压缩腔经常开阀7、节流阀9进入轮缸10，实现系统增压。经ABS系统的ECU单元的计算判断，若需要轮缸10制动压力降低，则发出控制信号，使常开阀7关闭，同时启动回流泵电机3并打开常闭阀11，使制动液流向低压蓄能器12，或流回主缸2，使轮缸压力降低，制动力减小。若轮缸压力需要保持，则ECU发出控制信号，将常开阀7关闭(通电)，常闭阀11保持关闭状态(不通电)，则轮缸10内的制动液被封闭，制动压力保持不变。通过改变电磁阀开关切换，改变制动液的通路，从而形成增压、保压和减压3种压力状态。

图1 1/4车体ABS系统示意图

ABS工作过程中，换向阀常处于频繁切换过程。当换向阀突然换向时，油液速度突然变化，压强快速升高或降低，引起冲击波动，压力冲击波作用于液压轮缸，从而引起振动与噪声。若不考虑液压油黏度变化的影响，冲击波的传播速度C［2］:

式中:K'为液压油的等效体积弹性模量(Pa)，K为液压油的体积弹性模量(Pa)，ρ为液压油的密度(kg/m3)，E为管道材料的弹性模量(Pa)。

当电磁换向阀突然关闭时，管道内的液体运动突然停止，根据能量守恒定律，液体的动能将转化为液体的弹性能，即

所以

制动轮缸的运动部件的运动速度取决于流量，当突然改变流量时(如阀口关闭)，由于液压油的惯性作用，产生液压冲击。冲击压力最大升值Δp为液压油惯性冲击和运动部件惯性冲击产生的压力升值之和，即:

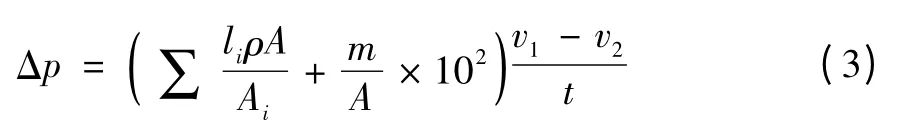
式中:A为液压缸的活塞面积(m2)，li为液压油第i段管道的长度(m)，Ai为液压油第i管道的有效面积(m2)，m为当缸体不动，活塞运动时，折算到活塞上的运动部件质量(kg)，v1、v2分别为活塞变化前后的运动速度(m/s)，t为活塞由速度v1到v2的变化时间(s)。

因此，液压冲击的实质是液体动能的转变，它与冲击波的传播速度C有关，传播速度C决定了能量的变化大小。

2 ABS系统建模与振动分析［3-4］

AMESim(系统仿真平台)是系统工程建模与仿真平台［5］，它提供了系统工程设计的完整平台，在此平台上，工程师可以建立复杂的多学科领域系统模型，进行仿真计算和分析。目前，AMESim已经成为用于车辆、越野设备、航空航天以及重型设备工业的多学科领域，包括流体、机械、热分析、电磁以及控制等复杂系统建模和仿真的优选平台［6］。

根据图1建立ABS系统AMESim模型(如图2所示)。

图2 1/4车体ABS系统AMESim仿真模型

主要步骤如下:

(1)忽略一些不重要的部分，将系统主要物理结构分为最小的元素，每个小元素用AMESim功能模块来代替，其中图中轮缸10为封装后的超级元件;

(2)模型中的MCU为MATLAB/Simulink建立的ABS控制器，其控制方法为逻辑门限值控制。输入信号包括:制动转矩、四轮轮速(本模型针对1/4车体，只需输入左前轮轮速信号)和车速信号，ABS控制器产生的压力调节信号输出到AMESim车辆模型中的ABS系统(1/4车体)，实现制动管路压力的调节与控制。Simulink所建立的ABS控制器嵌入AMES-im模型，实现联合仿真;

(3)在软件界面中连接所有的模块并设置参数;

(4)将建好的模型放进搭建的系统中仿真并分析结果。

利用图2所示的仿真模型在AMESim环境进行仿真试验，控制器采用MATLAB/Simulink建立的逻辑门限值控制器。主要分析数据是液压缸的位移、速度、加速度与管道中的压力波动。仿真时间为100 s，仿真步长为0．001 s，换向阀打开时刻为10 s，整定系统压力为22．3 MPa。仿真试验得到换向阀打开时的压力曲线(图3)、活塞位移曲线(图4)、活塞速度曲线(图5)和活塞加速度曲线(图6)。

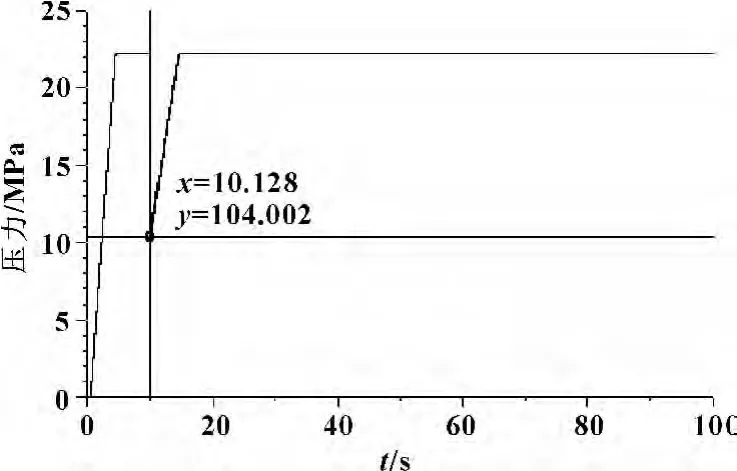
图3 原ABS系统压力曲线

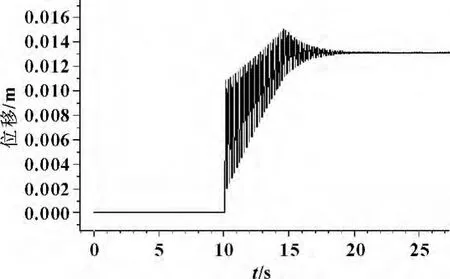
图4 原ABS系统活塞位移曲线

图5 原ABS系统活塞速度曲线

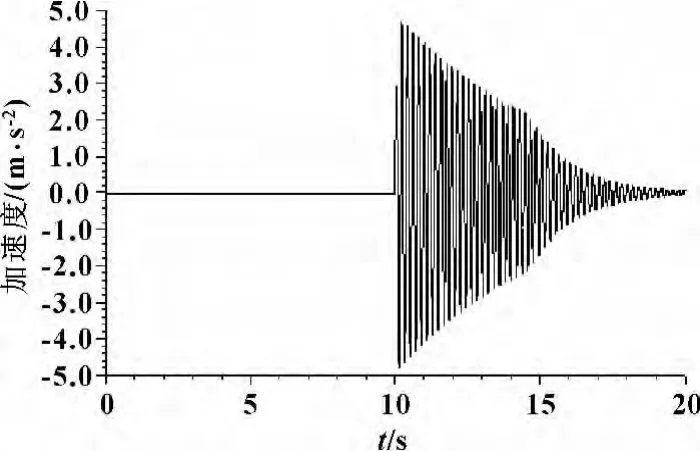
图6 原ABS系统活塞加速度曲线

在换向阀工作时，系统压力经过0．128 s，系统压力从22．3 MPa骤降到10．400 2 MPa，在14．618 s恢复到22．198 4 MPa。这种液压冲击对活塞位移影响如图3所示，说明原系统的抗冲击性能很差。可见:在ABS液压系统中，当换向阀突然打开后，由于液压泵无法满足瞬时的大流量需求，系统压力骤降，出现换向压力冲击。通过速度及加速度曲线表明液压冲击波的传递、反射、液流方向的变化将反复进行，直到耗尽引起冲击的能量，冲击现象才会结束。

3 改进后的ABS系统的仿真试验及性能分析

通过上述试验，说明原ABS系统在换向阀工作时，存在明显的液压冲击，由公式(3)说明，冲击压力最大升值Δp与流速v成正比，v=q/t。所以换向阀打开引起的流量的突变是引起液压冲击的根本原因。而原系统的换向阀打开或关闭很直接的，阀的开闭是非连续的，存在明显的流量突变。所以改进系统用伺服阀替换原系统的换向阀，用基于压力反馈的PID控制结合逻辑门限控制实现伺服阀的打开与关闭，实现流量的连续调节。

改进后的ABS系统AMESim模型如图7所示。

利用图7所示的仿真模型在AMESim环境进行仿真试验，控制器采用MATLAB/Simulink建立的基于压力反馈的PID控制结合门限值控制的ABS控制器［7］。经仿真试验，得到改进后的ABS系统在伺服阀打开时的压力曲线如图8所示，活塞位移曲线如图9所示，活塞速度曲线如图10所示，活塞加速度曲线如图11所示。

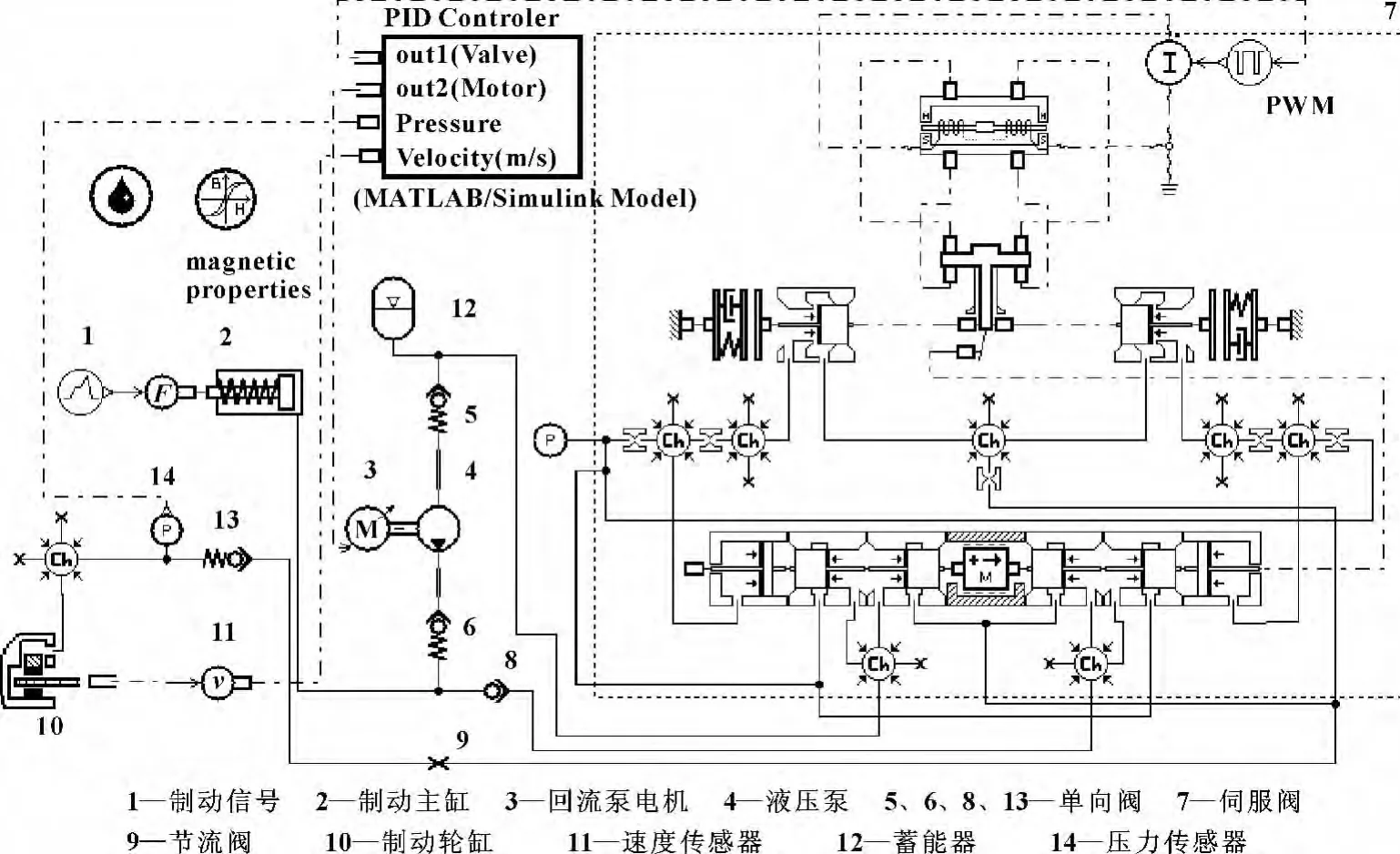
图7 改进后的ABS系统AMESim模型

图8 改进后的ABS系统压力曲线

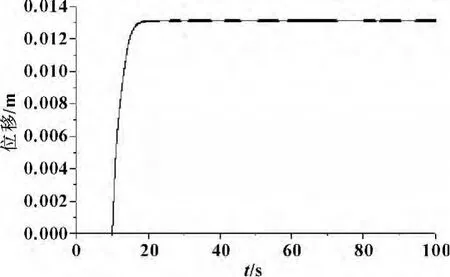
图9 改进后的ABS系统活塞位移曲线

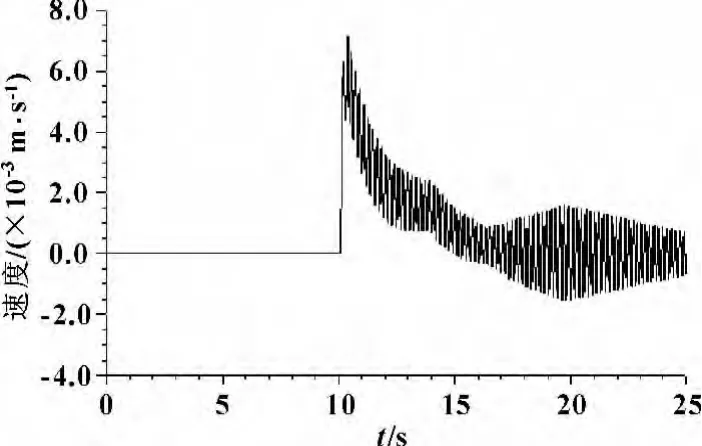
图10 改进后的ABS系统活塞速度曲线

图11 改进后的ABS系统活塞加速度曲线

如图8所示，伺服阀的打开信号输入时刻为10 s，经过1．549 s，系统压力从22．3 MPa降低到18．042 8 MPa，到13．884 s，又升高到22．198 4 MPa。液压冲击较缓慢，冲击明显减弱。如图9所示，活塞位移曲线非常平缓。对比图5与图10，原系统速度最大变化为0．3 m/s，改进后的系统速度最大变化为0．004 m/s，表明活塞速度的突变明显减弱。对比图6与图11，原系统的加速度变化的最大幅度为10 m/s2，改进后的系统的加速度变化的最大幅度为0．1 m/s2，加速度的突变明显减弱。

4 结论

通过原ABS系统与改进后ABS系统的试验对比，在换向阀打开的瞬间，改进系统的压力变化非常平缓;活塞速度变化由原来的0．3 m/s降低到0．004 m/s;活塞加速度变化由原来的10 m/s2降低到0．1 m/s2。试验结果表明:改进的ABS系统利用伺服阀替换传统换向阀，用基于压力反馈的PID控制结合门限值控制代替单纯逻辑门限值控制方式，用连续流量控制代替非连续流量控制，由于伺服阀的响应快，反馈信号的频率高，相当于用伺服阀高频的振荡来抵消了压力冲击，系统始终保持稳定，抗冲击性能明显提高。

［1］杨风和，孙伯．改变DRP控制逻辑以解决ABS阀体噪声［J］．汽车技术，2012(7):37-39．

［2］马宪亭，尹新爱．液压冲击计算与控制方法［J］．煤矿机械，2009，30(3):157-158．

［3］MODAK J P，BELKHODE P N，BODHANKAR D，et al．Modeling and Analysis of Front Suspension for Improving Vehicle ride and Handling［C］．First International Conference on Emerging Trendsin Engineering and Technology，2008:731-734．

［4］DASGUPTA K，WATTON J，PAN S．Open-loop Dynamic Performance of a Servo-valve Controlled Motor Transmission System with Pump Loading Using Steady-state Characteristics［J］．Mechanism and Machine Theory，2006(41):262-282．

［5］李吉，李华聪．仿真软件AMESim应用研究［J］．航空计算技术，2006，36(1):56-58．

［6］付永领，祈晓野．AMESim系统建模和仿真［M］．北京:北京航空航天大学出版社，2006．

［7］WUMingchin，SHIH Mingchang．Simulated and Experimental Study of Hydraulic Anti-lock Braking System Using Sliding-mode PWM Control［J］．Mechatronics，2003，13(4):332-350．