基于STM32光栅细分算法在指示表检定仪上的应用

刘川，张恕远

(西华大学数控研究所，四川成都 610039)

0 前言

指示表检定仪是用来检定指示表准确度的仪器，在仪表生产企业和计量检定技术机构，需要对指示表各项技术指标进行检定［1］，要求检定仪实现0．1μm的分辨率，目前检定仪多用光栅尺作为位移传感器实现检定。现代光栅是用精密的刻划机在玻璃或金属片上刻划而成的，由于受加工工艺的限制，刻线条数受到限制［2］，对光栅信号可逆计数获得光栅位移［3］，但分辨率低。对于本系统使用光栅尺的栅距为20μm，要求实现0．1μm分辨率，可用常规硬件电路对信号进行可逆计数或细分［4］，或用模数转换结合硬件查表［5］细分，但电路复杂且难达到要求。为了满足要求，降低成本，简化电路，本文作者提出了一种实现光栅位移细分测量的方法。该方法省去了计数电路和细分电路，由单片机采集光栅的两路正交正弦信号进行数字滤波和特征值提，然后细分和误差补偿，实现了对光栅尺位移的高精度细分测量。

1 系统硬件结构

系统硬件结构如图1所示，光栅细分系统以STM32F103RBT6为主控单元，主要是它使用ARM内核，主频较高、处理能力较强，满足细分的采集计算和显示的动态要求。

图1 系统硬件结构

信号调理选用单电源仪表运算放大器AD623，对四路光电池信号的两两差分放大后得到两路互差90°的正弦信号。由于放大器电源电压为5 V单电源，为不失真地放大出光栅信号，选用TL431输出2．5 V电压作为四路光电池的信号的基准电压，对信号差动放大后可以得到以2．5 V作为基准上下波动的两路正交正弦信号，便于AD转换和数据处理。

在信号采集方面，指示表检定仪的光栅信号实测频率小于20 Hz，为实现200细分，在采样过程中不丢失可逆计数判断点，在一个周期内至少要采样200个点，AD转换速度必须大于4 000 Hz。所以选用8位的AD7821模数转换器，AD7821的1 MHz转换速率满足要求。在转换过程中为避免电源电压的波动影响AD转换准确度，选用高精度的电压基准芯片AD586作为模数转换器的电压基准源。系统中外接了键盘对采样和相关参数进行设置，用液晶显示屏显示光栅的位移。

2 细分原理及算法

经过AD623信号调理后的两路互差90°的正弦信号可以用sinθ和cosθ表示，sinθ和cosθ中的任意信号的一个完整周期代表着光栅尺的一个栅距的位移，光栅尺停止运动时的相位与上一个完整半周期结束之间的相位构成非完整半周期［6］。为了得到分辨率较高的位移，就需要知道非完整半周期对应的相位。如果用d表示非完整半周期位移，用D表示1个光栅尺栅距，用X表示光栅尺位移，那么光栅的位移可以用如下的公式表示:

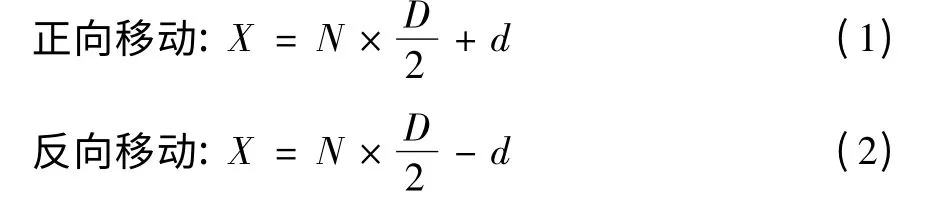
从公式(1)可知要计算位移X，需要对N进行可逆计数，并确定非完整半周期的相位。软件实现可逆计数需要对光栅尺的移动辨向，根据移动方向的不同对半波进行可逆计数。可逆计数时选定sinθ作为计数波形，cosθ辅助辨向，按照表1逻辑可实现可逆计数。

表1 可逆计数逻辑

表1中sinθ的过零方式的“↓”和“↑”分别表示从上往下过零和从下往上过零(sinθ＞0为上，sinθ＜0为下)。表1包含了sinθ的两种过零方式和cosθ正负值的组合成的4种情况。

半周期可逆计数对光栅信号进行了2细分，为实现200细分还需要对半周期进行100细分，因而需要确定半周期信号的相位。由于正余弦在波峰和波谷处幅值变化不明显，选取一路AD采样值求反正弦不能准确地确定相位［5］，因此要实现对两路信号的高精度细分需要对两路信号重构，从图2可以看出-几乎是线性变化的三角波，因此可以将两路信号重构为函数［7］:

图2 正向时的细分原理图

三角波是一个线性的函数，所以在做细分时可以按照恒定的线性关系来计算当前的相位值完成细分。从图3中可以知道半周期中合成的细分函数是对称的，所以半周期的100细分可以改为对1/4周期进行50细分。设由线性关系计算的细分值为x，则细分算法如表2所示。表2中判断光栅尺停止时候的相位，需要根据可逆计数时得到的运动方向和两路信号的采样值来计算。

表2 细分算法

根据表2的逻辑关系，在仪器调试时将两路光栅信号调整为相同的峰峰值，由单片机计算出峰峰值PK。当光栅尺停在图2中的点A处时，设光栅尺此时位移为XA，可以得到:

因为光栅为正向运动，在A点时sinθ＜0，cosθ＞0，根据表2可以得到

为了计算的方便需要将Y(θ)向上平移PK/2，让Y(θ)所有取值为正，得到平移后的函数为:其中公式(5)中的x为:

将公式(7)代入公式(5)，然后再将公式(5)代入公式(4)，可以得到在点A时的位移为:

为了保证精度需要验证将Y(θ)作线性函数计算引入的误差是否满足精度要求，因为正余弦为周期信号，在分析误差时可以简化为对一个周期进行分析，在一个周期之内对应Y(θ)的三角波为设为Y1(θ)，Y1(θ)为:

用MATLAB将Y(θ)和Y1(θ)绘制到同一图中可以看出两者不是完全重合的，误差是否在分辨率之内需要对误差的最大值进行计算，误差函数为:

在一个周期内误差为:

U(θ)中的误差曲线如图3所示。

图3 误差分析图

用MATLAB计算出误差U(θ)最大的绝对值约为4．22%，对一个周期进行200细分，细分分辨率为0．1μm，对1/4个周期要进行50细分，所以误差绝对值的最大值为:

U(θ)max=D/4×0．1×4．22%

U(θ)max=0．211μm

由此可知用Y(θ)对信号线性细分误差最大为0．211μm，该值大于了0．1μm，所以为达到精度需要误差补偿，对误差建表格存入单片机Flash，以查表的方式对误差进行补偿。

3 实验研究

将硬件电路和仪器机械部分调试好后，在信号调理输出端可以得到如图4左半部分所示的两路相位互差90°，幅值基本相等的正弦信号，其构成的李萨茹图如图5的右半部分所示。

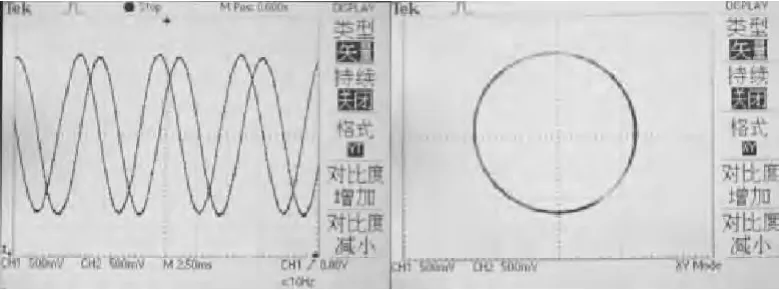
图4 信号调理后的光栅信号

由于得到的两路信号不是理想的正弦信号，在预处理之前用STM32的库函数中自带的FIR低通数字滤波器对信号进行了滤波。因为在硬件电路和机械上不可能将两路正弦信号都调整到绝对的相位互差90°和幅值相同，所以在软件部分需要对信号进行预处理来调整相位和幅值。如果是首次使用仪器，需要对信号进行采样提取特征值，且将特征值存入Flash便于以后直接读取特征值进行预处理。

由数字滤波和预处理要求，以及表1和表2的逻辑关系，编写程序到STM32中对光栅位移细分测量，为验证算法是否正确且误差是否满足要求，实验选用了比0．1μm更高分辨率和精度的激光干涉仪检验测量数据。实验设备如图5所示，本次实验用Renishaw公司的激光干涉仪ML10测量光栅的位移与文中设计的细分系统测量的位移对比，在对比实验时将激光干涉仪的分辨率调整到0．01μm。

图5 实验设备

实验对一个周期的莫尔条纹采集了一系列点，以激光干涉仪测量的位移作为横坐标，激光干涉仪测量值与细分系统测量值之差作为纵坐标，绘制出误差曲线如图6所示。

图6 误差曲线

由图6的误差曲线可以看出，在一个周期内最大误差为0．05μm，小于分辨率0．1μm，细分算法达到了细分精度要求。

4 结束语

以STM32F103RBT6作为处理单元，以软件的方法实现光栅信号的可逆计数和细分已经应用到计量行业的指示表检定仪上。用软件的方法实现20μm栅距的200细分，编程计算稍微复杂，但是硬件电路简单可靠，且成本低，在实际使用中效果良好，细分误差满足光栅式指示表检定仪规程的要求。

［1］王倩．光栅式指示表检定仪及其检定［J］．中国计量，1999(6):36-38．

［2］李燕青，郝德阜．衍射光栅制造技术的发展［J］．长春理工大学学报，2003，26(1):66-68．

［3］刘晓军，宋浩．基于偏振相移的干涉条纹细分原理［J］．华中科技大学学报，2008，36(6):4-6．

［4］NORBERT C Cheung．An Innovative Method to Increase Resolution of Optical Encoders in Motion Servo System［C］．IEEE 1999 International Conference on Power Electronics and Drive Systems，PEDS．99，Hong Kong，1999．

［5］KIM Jun-Chan，KIM Jang-Mok，KIM Cheul-U．Ultra Precise Position Estimation of Servomotor Using Analog Quadrature Encoders［C］．Applied Power Electronics Conference and Exposition，APEC．06，Twenty-First Annual IEEE，2006．

［6］刘柯，宋金城，陈秀政．基于TMS320F2812的光栅细分卡的设计［J］．红外与激光工程，2008，37(S1):242-246．

［7］李怀琼，陈钱，庄小栋．新型光栅信号数字细分技术及其误差分析［J］．电子测量与仪器学报，2001，15(3):71-75．