基于Python的多波束测深数据压缩研究

张明希，许捍卫,于艳超，俞礼彬

（1. 河海大学 地球科学与工程学院，江苏 南京 210098）

基于Python的多波束测深数据压缩研究

张明希1，许捍卫1,于艳超1，俞礼彬1

（1. 河海大学 地球科学与工程学院，江苏 南京 210098）

在曲线数据压缩的垂距限差法基础上，引入总体最小二乘算法对多波束测深的ping条带数据进行压缩，利用Python工具库实现总体最小二乘压缩算法并集成到ArcToolbox中。与传统道格拉斯-普克压缩算法具有接近的压缩比，但精度更高，能够在整体上更好地表示原始数据。

多波束数据;抽稀;总体最小二乘；Python

多波束测深系统是一种高效、高精度的水下地形测量系统，数据繁杂，即使单个ping也能产生几兆数据，对多波束测深数据的压缩处理非常重要。多波束测深系统沿着测线逐ping观测，并以ping为顺序存储，可以从Ping数据的压缩入手。关于数据压缩问题，国内外学者发展了许多算法。道格拉斯-普克算法（RDP）从整体上对曲线段进行考虑，通过保留特征点、删除冗余点来达到压缩目的[1]。总体最小二乘（TLS）方法是近年发展起来的能同时顾及观测值误差和模型系数矩阵误差的数学方法[2]。与RDP不同的是,TLS算法没有简单地删除距离误差小于限差的点, 而是略微放松对端点的精度要求, 通过TLS作直线拟合,从而提高曲线压缩的精度，在整体上最优逼近原始曲线。卢银宏等[3]综合利用RDP算法和TLS算法来压缩多波束测深数据，采用Matlab仿真二维ping数据进行压缩处理，忽略了当曲线的曲率很大时，两条拟合直线的交叉点可能会远离原始曲线的情况。本文基于ArcPy站点包和开源Python工具库，以Python作为脚本语言，开发了多波束测深三维ping数据点抽稀算法，具有易用性和重用性特点。

1 Python空间数据处理特点

Python语言作为稳定的动态脚本语言与ArcGIS高度集成，其灵活性和重用性可以方便实现地理空间数据的处理流程[4]。目前，ArcGIS10．0已集成基于Python的ArcPy站点包，可理解为ArcGIS的Python API。ArcPy提供了大量类和函数，可以轻松执行ArcGIS工具箱中的工具，并创建原生对象，如几何、栅格、空间参考等[5]。

另一方面，Python具有高级的内建数据结构，优秀的科学计算扩展库SciPy、NumPy（包括科学计算、统计分析、可视化等模块），高效的空间分析开源库GDAL、Shapely等。其中SciPy包含的Python模块有最优化、线性代数、积分、插值、特殊函数、快速傅里叶变换、信号处理和图像处理、常微分方程等函数[6]。Shapely库是针对平面几何对象的空间分析工具。基于点集理论，其将几何对象分为点、线、面3种类型，每种数据类型又有3个属性：内部集、边界集、外部集。Shapely以Python风格的代码形式访问GEOS库，将PostGIS的一般操作用Python语言加以实现，适合处理一些非常规的地理空间数据问题。

2 基于Python的总体最小二乘点抽稀

2.1 总体最小二乘直线拟合模型

传统最小二乘法拟合直线时，一般令直线方程为：

其中，x，y是测点坐标；a，b为待估参数。最小二乘法认为测量误差都存在于y中，而x没有误差或在进行平差时不予考虑。则误差方程可以表示为：

按最小二乘准则，得出其最小二乘解为：

一般认为，观测值y的获取方法相同，因此P为单位阵。

最小二乘只认为观测值y含有测量误差，事实上x、y均是采用测量方法获取的，按照总体最小二乘思想，应该对观测值x和y都进行改正。考虑到观测值x的误差，则条件方程为：

写成矩阵形式为：

其中， Vy为y的改正数；EA为系数阵A的改正矩阵。由于系数阵里含有固定列，运用混合总体最小二乘的迭代解法[7],求出参数a与b。

总体最小二乘直线拟合算法需要在SciPy的线性代数库linalg基础上，利用NumPy丰富的数组处理函数，按照总体最小二乘的迭代解法，重新编写Python脚本计算。

2.2 基于总体最小二乘的多波束数据点抽稀算法

RDP算法在给定限差情况下的逼近精度不高。如图1，当采用RDP算法对所示曲线数据压缩时，会得到线ABC。在保留点AB之间，被删除的点全部位于保留直线的一侧；在保留点BC之间，被删除点也全部位于保留直线的一侧。显然，用ABC表示原始数据具有明显的偏差，且均方误差较大。如图1a，采用基于TLS的分段直线拟合算法，对AB和BC之间的原始点分别作直线拟合，得到两条直线A′B′、B′C′，它们相交于B′。此时，利用A′-B′-C′代替A-B-C，可以提高对A、B和C点的压缩精度。但在个别情况下，如图1b，曲线的曲率很大时，两条拟合直线的交叉点可能远离原始曲线，明显偏离了原曲线的形状。

图1 直线拟合和交叉点远离原始曲线的处理

利用多波束测深的ping点数据，每个ping的相邻数据点由相邻波束脚印的中心确定，每个ping描述了某个横向的地形剖面，其x、y、z坐标可映射到二维平面。基于道格拉斯-普克的总体最小二乘三维点抽稀算法的基本步骤如下：

Step1：将多波束测深ping点三维坐标（x，y，z）变换为二维曲线坐标（dx，dy）。计算ping条带上某点O到空间直线AB（ping条带上的首尾点）的垂足坐标N（xn，yn，zn），然后求得N到点A和C的距离dx、dy，其中A（x1，y1，z1）、B（x2，y2，z2）为：

Step2：利用RDP算法对曲线坐标作压缩抽稀，选取抽稀后的特征点（Mx，My），并标记特征点所对应的索引值index。

Step3：搜索index和index+1中所包含的二维曲线点坐标对。考虑到TLS至少需要3个点坐标，当点坐标对数大于2时，利用TLS求出系数a、b。遍历所有index，求出直线拟合的交点坐标集（Hi，Hj）（i，j=1，2，…），记录其序号。

Step4：计算直线拟合的交点坐标（Hi，Hj）和特征点（Mx，My）间距离d。如果d大于限差ε，将直线拟合交点坐标替换成特征点，再运用基于Shapely库函数中的曲线intersection方法求出拟合直线段和原始曲线的交点。若某段出现多个交点，排序得出距特征点最近的交点，并补充到直线拟合交点坐标集中；否则只保留直线拟合交点坐标。

Step5：用步骤4得到的二维点集，解算空间平面坐标方程，反算得到抽稀后的三维ping点数据。

算法用Python脚本实现后，添加到ArcToolBox中，如图2。

图2 总体最小二乘算法点抽稀工具界面

2.3 实 验

选取某江水下地形多波束测深数据ping条带数据做测试，验证算法的有效性和正确性。该ping带含有62个测深点。用ArcToolbox中的自定义点抽稀工具脚本进行实例计算。

根据国际海道测量规范s44 特等测量的精度要求,抽稀阈值设为0．26 m[8]。图3显示了垂距限差取0．26 m时，分别采用道格拉斯-普克算法和分段总体最小二乘的压缩效果。其中蓝色实线代表原始ping数据，黑色点表示RDP算法抽稀效果，红色点表示TLS点抽稀效果。

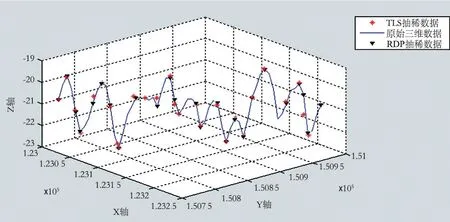
图3 点抽稀效果图

为评定算法的抽稀精度，计算RDP算法和TLS算法的均方误差，公式为其中di表示原始曲线上第i个点到压缩后曲线的垂直距离，n表示总点数。垂距限差分别取0．26、0．5、0．1进行测试。TLS和RDP的压缩比近似相等，均方根误差为当垂距限差较大时,TLS点抽稀算法比RDP算法精度提高更明显，能更好地逼近原始数据。

信息科学版,2013,38(7):850-856

[3] 卢银宏,岳东杰，宋飞凤．基于总体最小二乘的Douglas-Peucker算法在多波束测深数据抽稀中的应用[J]．水利与建筑工程学报,2012,10(2):4-5

[4] 彭海波,向洪普．基于Python的空间数据批量处理方法[J]．测绘与空间地理息,2011,34(4):81-82

[5] Dobesova Z．Programming Language Python for Data Processing[C]．International Conference on Electrical and Control Engineering (ICECE), 2011

[6] 张若愚．Python科学计算[M]． 北京：清华大学出版社，2012

[7] 鲁铁定,周世．总体最小二乘的迭代解法[J]．武汉大学学报：信息科学版,2010,35(11):1 351-1 354

[8] 夏伟,黄谟涛,刘雁春,等．Douglas-Peucker算法在多波束测深数据抽稀中的应用[J]．测绘科学,2009,34(3):159-160

[1] 杨云,孙群,朱长青．曲线数据压缩的总体最小二乘算法[J]．西安电子科技大学学报：自然科学版,2008,35(5):946-950

[2] 王乐洋,许才军． 总体最小二乘研究进展[J]．武汉大学学报：

P229.3

B

1672-4623（2014）04-0117-03

10.11709/j.issn.1672-4623.2014.04.041

张明希，硕士，主要研究方向为地理信息系统开发与应用。

2013-10-10。

项目来源：国家自然科学基金资助项目（41101374）。