内蒙古地区气温空间插值模拟方法研究
2014-04-18王志恒朱衍达
王志恒,朱衍达
(1. 天津城建大学 地质与测绘学院, 天津 300384;2. 北京师范大学 资源学院, 北京 100875;3. 舟山甬舟集装箱码头有限公司, 浙江 舟山 316033)
内蒙古地区气温空间插值模拟方法研究
王志恒1,2,朱衍达3
(1. 天津城建大学 地质与测绘学院, 天津 300384;2. 北京师范大学 资源学院, 北京 100875;3. 舟山甬舟集装箱码头有限公司, 浙江 舟山 316033)
以内蒙古自治区为研究区,采用反距离权重法、样条函数法和普通克里金法对研究区119个气象观测站点的气温数据进行空间插值,结果表明,普通克里金法由于能够最优地描述气温在空间上的连续性变化特征,插值精度最高;反距离权重法插值精度次之,但其模拟结果趋于产生牛眼模式,且结果不能外推;样条函数法由于受到边界效应的影响,插值精度最低。
空间插值; 气温; 克里金法; 反距离权重法; 样条函数法

气温是进行雪灾监测、评估和预警的重要气象因素[1],而准确获取任意位置的气温数据,对提高内蒙古地区雪灾预测预报的精度具有重要意义。但是,由于气象站点布设有限[2],所获得的气温数据在空间上是离散的,通常需基于已有站点的观测值进行估算,来得到全局空间范围内各个空间位置的气温数据。国内外学者在气象要素空间插值分析方面开展了大量工作。Ashraf等[3]选取分布在科罗拉多州、堪萨斯州等地的17个气象站点,分析气温、相对湿度以风速等气象要素的最佳插值方法,发现克里金法最优。殷嘉霖等[4]通过对多种插值方法的比较,发现局部多项式法对湖南省年平均降雨量的插值精度最高。彭洋等[5]通过实验证明,反距离权重法在模拟安徽省年平均降雨量空间分布上具有较高的精度。可以看出,在实际应用中,没有适合任意插值对象的最优插值方法,要根据待插值要素和研究区的特点,通过对比分析,筛选出研究区内适用于待插值要素的最优空间插值方法。本文选取内蒙古自治区作为研究区,基于119个气象观测站的气温数据,分别选取反距离权重法、样条函数法和普通克里金法3种方法进行空间插值,并通过交叉检验,分析不同插值方法对研究区气温的估算精度,进而确定该地区气温要素空间插值的最优方法。
1 研究区概况
内蒙古自治区地处我国北部边疆,由东北向西南斜伸,呈狭长形。全区总面积118.3万km2,占我国土地面积的12.3%。气候主要以温带大陆性季风气候为主,春季气温回升迅速,大风天气较多,夏季炎热而短促,降水比较集中,秋季温度剧降,霜冻往往来得很早[6]。由于具有丰富的草场资源,畜牧业历来是内蒙古的支柱产业。
2 研究基础
2.1 数 据
本研究选用的气温数据资料来源于内蒙古自治区119个气象站点2009年逐日气温观测数据,气象站点的空间分布如图1。
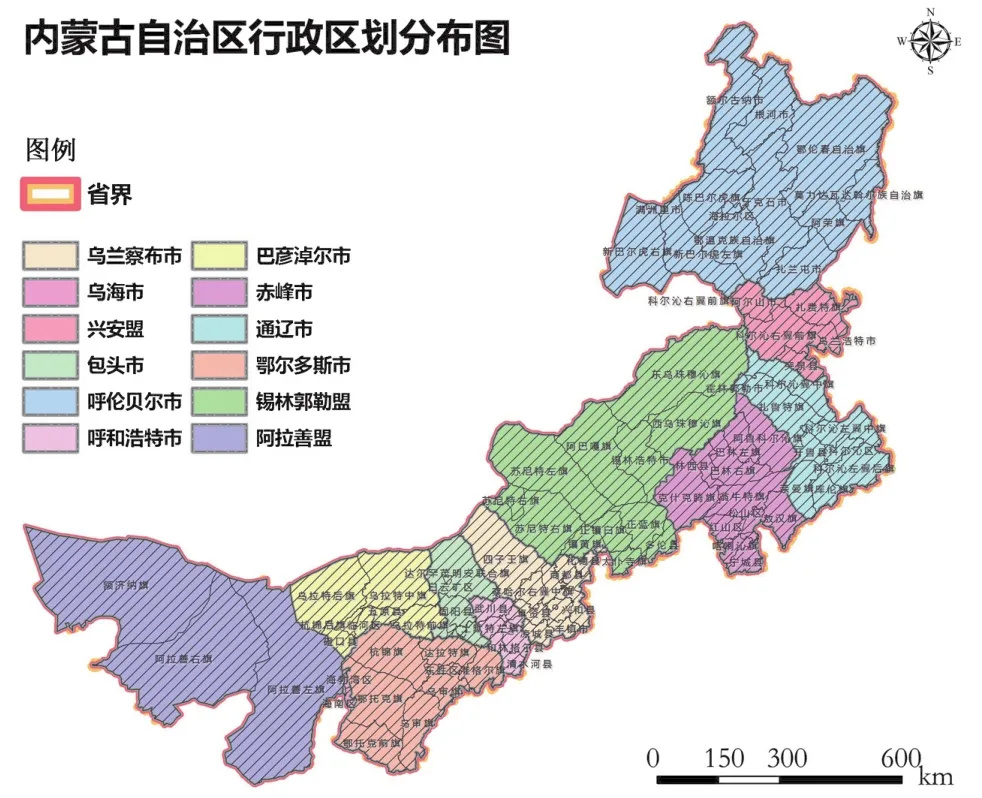
图1 内蒙古自治区气象观测站点空间分布图(审图号:GS(2002)310号)
2.2 空间插值算法
空间插值的基础是空间相关性,即空间位置越靠近,事物或现象的相似度就越高,反之,空间距离越远,就会越相异或越不相关[7]。
2.2.1 反距离权重法(IDW)
该方法以插值点和样本点之间的距离作为权重来进行加权平均,如式(1)所示:
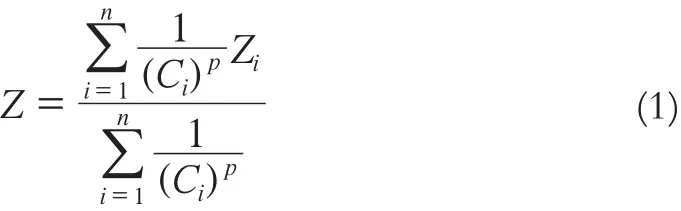
式中,Z为估算值;Zi为第i个样本点的观测值;Ci是估算点与第i个样本点的距离;p是指定的幂次;n为样本数。
2.2.2 样条函数法(Spline)
该方法利用最小化表面总曲率的数学函数生成恰好经过输入点的平滑表面[8],表示为:
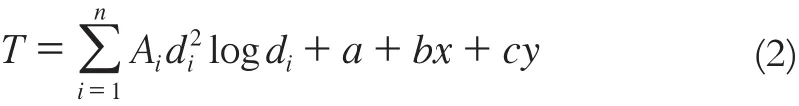
式中,T为待估计的插值要素值;di为插值点到第i个气象站点的距离;a+bx+cy为气温的局部趋势函数;x、y为插值点的地理坐标;Ai、a、b和c为方程系数;n为用于插值的气象站点数目。
2.2.3 普通克里金法(OK)
克里金法基于这样的一个假设,即被插值的某要素可以被当作一个区域化的变量来看待,该变量随所在区域位置的改变而连续地变化。其关键步骤是基于变异函数拟合空间上不同点属性之间的空间相关性,变异函数可表示为:
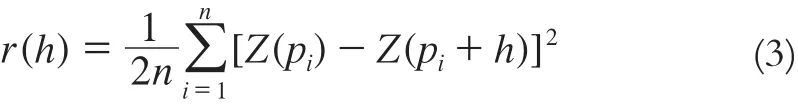
式中,r(h)为半变异协方差,值越大表明点与点之间的相关性越小;Z(pi) 和 Z(pi+h) 分别是Z(x)在空间位置pi和pi+h上的观测值;n为距离为h的采样点数。克里金法计算某点值的基本公式如下:
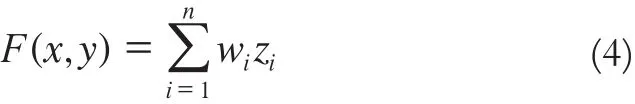
式中,n是集合中离散点的个数;zi是离散点的数值;wi是赋予每个离散点的权重。该权重可以通过求解联立方程组来获得:

2.3 精度分析方法
本研究采用交叉验证的方法检验各插值方法的空间模拟效果[9]。首先,预留部分气象观测点为检验站点,通过计算预测值与实测值间的误差来评价各种方法的优劣。假设Ti表示站点预测值,Tm为站点实测值,n为站点数,采用绝对误差(absolute error, AE)和相对误差(relative error, RE) 来分析单个检验点上的误差:


然后,采用平均绝对误差 (mean absolute error, MAE)和平均相对误差(mean relative error, MRE) 作为精度检验的标准。MAE反映样本数据估值的总体误差,定量给出误差;MRE通过反映不同数据量的误差相对值,定性地给出误差范围,效果更为直观。MAE和MRE越小,表明插值精度越高。计算式为:
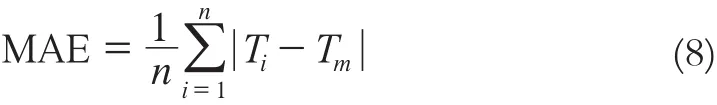
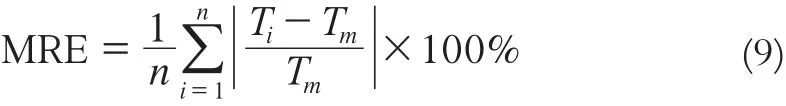
3 实验及结果分析
3.1 技术路线
3种插值方法对比分析的技术路线如图2所示。首先,在119个气象观测站中选取15个作为检验点,其余为插值点;然后,分别使用IDW、Spline和OK三种插值方法进行插值模拟;最后,基于MAE和MSE定量分析各插值方法的精度,确定适用于研究区气温要素的最优空间插值方法。
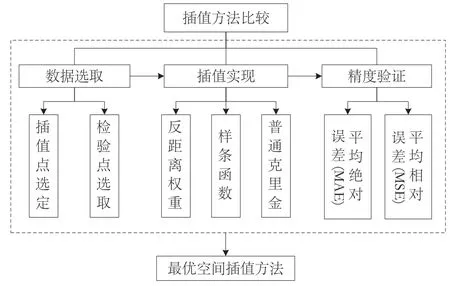
图2 研究技术路线
3.2 3种方法的插值结果及分析
基于插值选取的104个气象观测站数据,分别进行IDW、Spline和OK三种方法的空间插值,结果如图3所示。其中,图3a 为使用IDW的插值结果,最明显的特征就是出现了许多“牛眼”,显得非常突兀;图3b 为使用Spline的插值结果,温度范围由1.68 ℃到-34.41 ℃,远超过了样本点原来的数值范围,结果出现异常;图3c 为使用OK的插值结果,总体上比较平滑,模拟结果较接近真实情况。
3.3 交叉验证
3.3.1 检验点选取
按所在位置和海拔,从119个气象观测站中选出15个作为检验点,见表1。检验点选取应考虑以下原则:①所选检验点必须在内蒙古地区均匀分布;②所选检
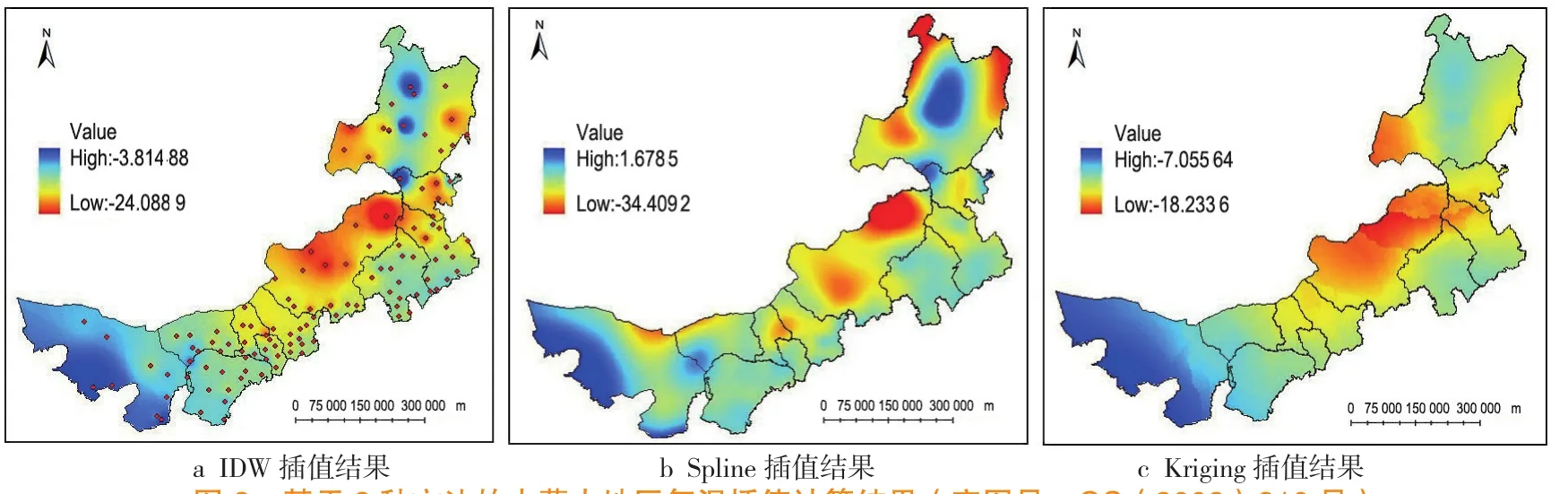
图 3 基于3种方法的内蒙古地区气温插值计算结果(审图号:GS(2002)310号)
验点基本上可以代表内蒙古地区各地的海拔特征。
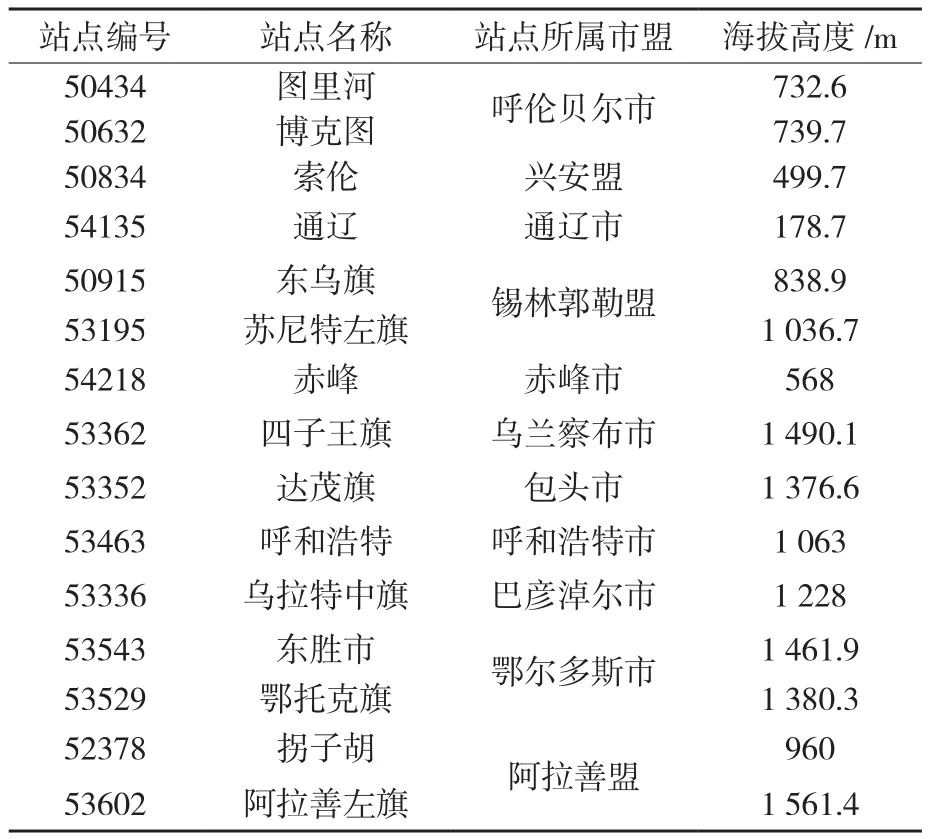
表 1 检验点列表清单
3.3.2 精度验证
插值模拟后,各检验点所处位置的预测气温值可以从插值计算结果中直接获得,并与检验点的实测值进行对比,见表2。基于式 (6)和式(7),可计算得到经过3种插值方法模拟后各检验点的预测结果与实测值的误差,如表3所示。
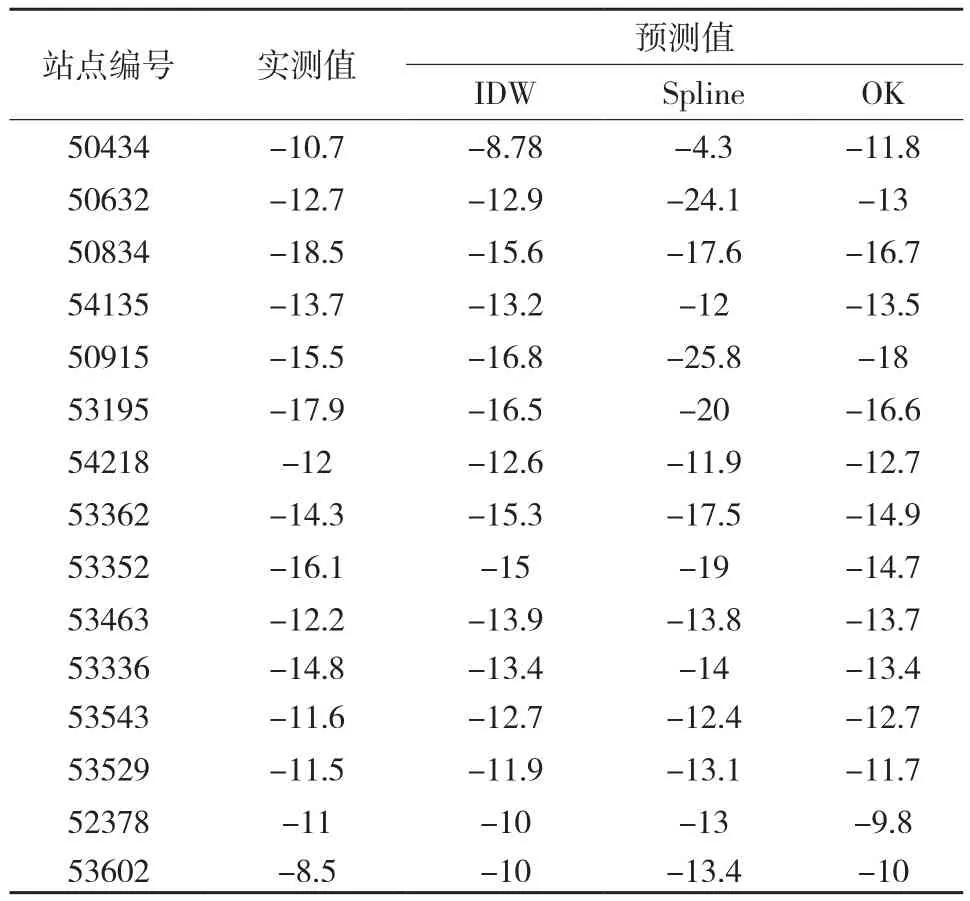
表2 检验点实测温度与预测结果对比分析表 /℃
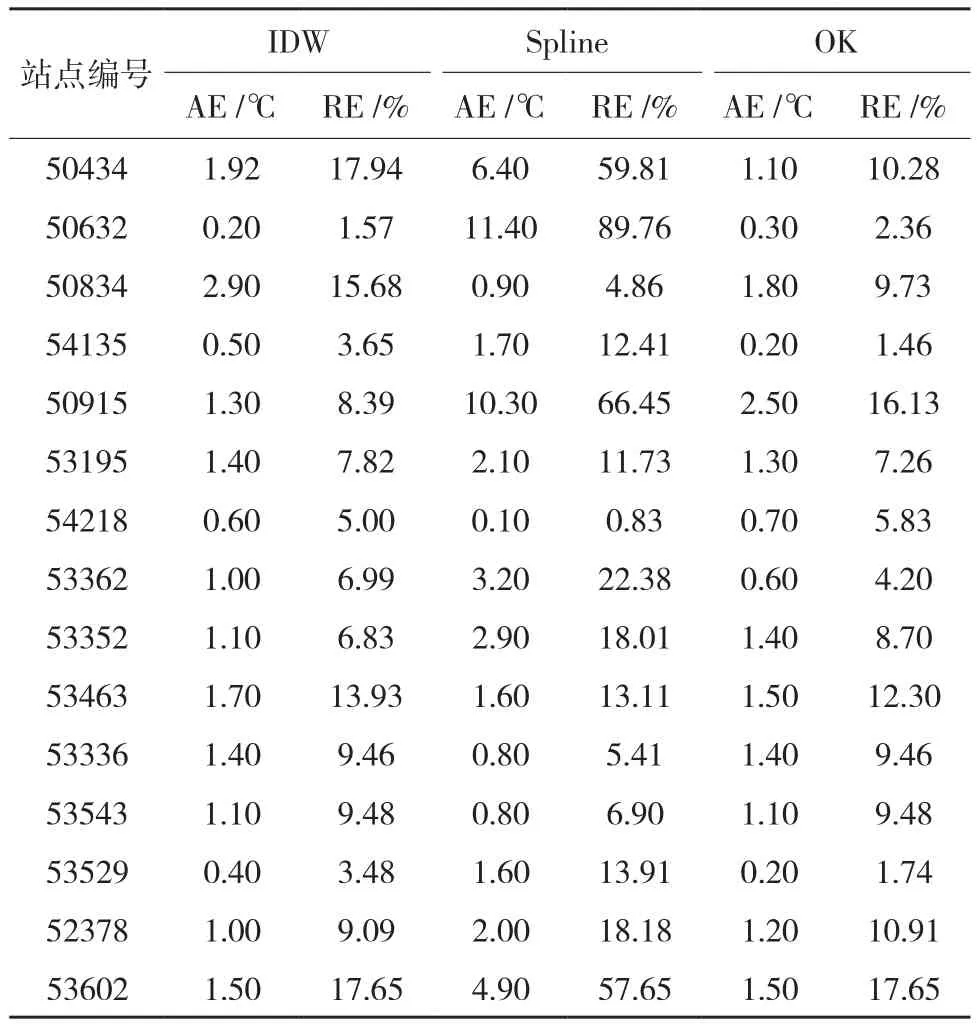
表3 检验点误差统计表
交叉验证的结果如表4所示。在3种插值方法中,MAE的排序为OK < IDW < Spline;MRE的排序为OK < IDW < Spline。

表 4 3种插值方法误差大小比较
可以看出,OK法获得了最低的MAE和MRE,说明内蒙古地区气温要素的空间分布具有自相关的特性,而OK法可以充分利用插值点和变异函数结构来模拟气温要素的空间分布特征,因此对于内蒙古地区的气温要素插值,OK法略优于其他2种插值方法。IDW法插值结果的精度略低于OK法,但也取得了较高的预测精度,这与内蒙古地区气象观测站数量较多、密度较高有关系。Spline法插值结果的精度远低于其他两种插值方法,这主要是由于拟合多项式严重依赖于插值数据,并容易受边界效应影响,因此在研究区域的边界,插值结果往往会出现异常值。
4 结 语
1)从分析结果来看,3种空间插值方法均能反映内蒙古地区气温的分布特征,而OK能够准确地模拟研究区气温空间分布的自相关特征,具有更高的插值精度。
2)通过交叉检验表明,OK和IDW的插值精度较为接近,但在实际应用中,OK能够提供外推和预测的误差估计,可以很好地逼近极值,而IDW适用于处理密集数据,不能外推,故不能对极值进行准确的预测;Spline由于只考虑局部变量,插值结果存在显著的边界效应,误差最大。
3)气温是一个受众多因素影响的复杂过程,若要进一步提高空间插值的精度,还需要引入更多的因素(比如地形条件、地理位置、站点密度等)来建立更为精准的气温空间插值预测模型。
[1] 康玲. 内蒙古地区雪灾分析[J]. 内蒙古气象, 2007(1): 10-11
[2] 王红霞, 柳小妮, 任正超, 等. 降水量的空间插值方法研究——以甘肃省为例[J]. 草原与草坪, 2012, 32(5) :12-16
[3] Ashraf M, Loftis J C, Hubbard K G. Application of Geostatistics to Evaluate Partial Weather Station Networks[J]. Agricultural and Forest Meteorology, 1997,84: 255-271
[4] 殷嘉霖, 屈创. 湖南省年均降水量空间插值模拟方法比较研究[J]. 甘肃科技, 2013, 29(1): 38-40
[5] 彭洋, 查良松. 安徽省降雨量空间分布方法[J]. 地理空间信息, 2010, 8(1): 67-69
[6] 银山, 香宝, 雷军, 等. 内蒙古自然灾害综合分区与评价[J].资源科学, 2002, 24(3): 31-35
[7] 邬伦, 刘瑜, 张晶, 等. 地理信息系统——原理、方法和应用[M]. 北京: 科学出版社, 2011
[8] Franke R. Smooth Interpolation of Scattered Data by Local Thin Plate Splines[J]. Computer and Mathematics with Appllications, 1982 (8): 273–281
[9] Seaman R S. Objective Analysis Accuracies of Statistical Interpolation and Successive Correction Schemes[J]. Aust Met Mag, 1983, 31: 225-240
P208
B
1672-4623(2014)04-0001-03
10.11709/j.issn.1672-4623.2014.04.001
2013-10-29。
项目来源:国家自然科学基金资助项目(41301468);国家科技支撑计划资助项目 (2012BAH33B03, 2012BAH33B05);民政部减灾和应急工程重点实验室开放基金资助项目 (LDRERE20120104)。
王志恒,博士研究生,讲师,主要研究方向为地理信息技术在灾害风险评估中的应用。
