基于Python的GPS高程异常拟合研究
2014-04-18于艳超许捍卫张明希
于艳超,许捍卫,张明希
(1. 河海大学 地球科学与工程学院,江苏 南京 210098)
基于Python的GPS高程异常拟合研究
于艳超1,许捍卫1,张明希1
(1. 河海大学 地球科学与工程学院,江苏 南京 210098)
考虑GPS高程异常具有一定的空间相关性,可将ArcGIS地统计中的确定性插值方法应用到GPS高程异常拟合中。结合Python脚本实现基于加权总体最小二乘的GPS高程异常拟合算法。结果表明,该算法的点位拟合精度和检核精度均优于ArcGIS地统计确定性插值。
GPS高程异常;地统计分析;总体最小二乘;Python

拟合方法是工程领域进行GPS高程转换的首选方案,其基本原理是在中小测区将似大地水准面看作平面或曲面,用多项式函数拟合法进行高程转换[1-3]。考虑到GPS三维坐标中平面坐标与高程以及GPS测量所得大地高与水准测量所得正常高的不等精度性,通过对观测向量以及系数矩阵定权,采用加权总体最小二乘(weighted total least-squares,WTLS)的GPS高程曲面拟合算法,无论数学的严密性,还是模型参数的精确性以及空间数据的适用性,均优于ArcGIS地统计中的确定性插值方法[4]。
Python作为一种通用脚本语言,可以像Matlab一样随写随运行[5]。从ArcGIS10.0开始,ESRI在所有产品中都集成了基于Python的站点包ArcPy。作为ArcGIS系统扩展和二次开发的语言,其灵活性和重用性可以很方便地实现空间数据的处理[6]。ArcPy提供了大量的类和函数,可以轻松执行ArcGIS工具,并创建原生对象,如几何、栅格、空间参考等[7]。本文基于Python,实现了基于加权总体最小二乘的GPS高程异常拟合算法。
1 加权总体最小二乘趋势面拟合算法
1.1 基于最小二乘的GPS高程异常拟合算法
GPS高程异常拟合的基本原理是在中小测区将似大地水准面看作一个连续的平面或曲面。本文采用二次多项式曲面拟合:
式中,a0~a5为待求参数。利用线性回归模型进行参数估计的Guass-Markov 模型为:
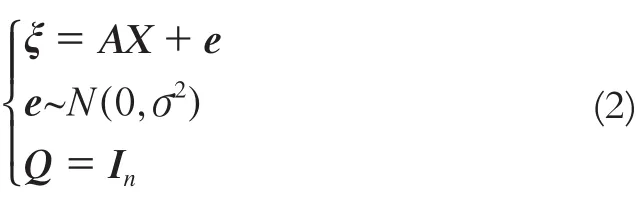
式中,

为拟合点数。
根据最小二乘估计准则,得最小二乘解为:

单位权中误差为:

1.2 加权总体最小二乘算法
从最小二乘算法模型与解算过程不难看出,最小二乘法只考虑了高程异常的误差,而未考虑系数矩阵的误差。然而,从组成系数矩阵A的元素可见,除了第一列,其他列均是与大地高坐标有关联的,忽略系数矩阵的误差不仅不符合实际,而且从理论上讲也是不够严密的。系数矩阵A中含有误差的模型[8]为:
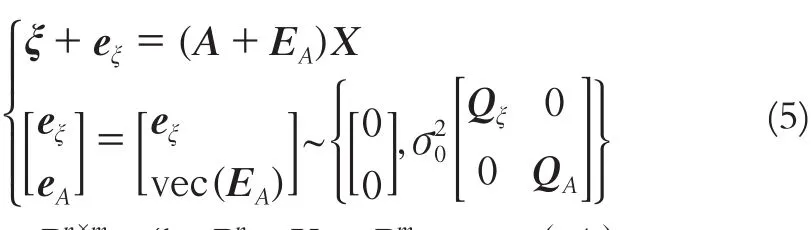
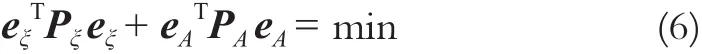
随机模型为:

GPS测量所得的三维坐标中平面坐标的精度要高于高程,且高程异常值为大地高与正常高之间的差值,这就导致平面点位X和Y的观测精度相当,而高程异常ζ的精度则不同。定义每个观测点之间相互独立且具有相同的平面测量精度,则σx=σy,系数矩阵A的列向量权阵表示系数矩阵中每列观测值之前的权比关系,也可以表示为不同类观测值之间的权比关系。所以,根据协因素传播律以及系数矩阵的数值形式,可得:
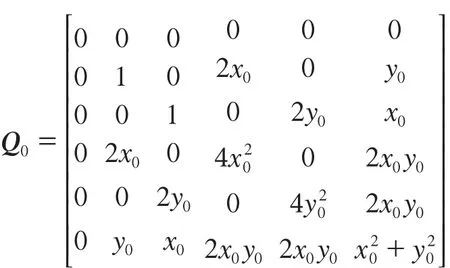
2 算例分析
本文选取某城市四等水准联测的58组城市E级GPS控制网高程测量数据为数据源,根据已知数据的点位坐标和大地高、正常高的测量值,计算高程异常。数据点分布在21.5 km×27.5 km的范围内,点位密度满足GPS高程异常曲面拟合的要求。高程异常值从0.656到1.769,变化范围较小。在进行曲面拟合时,为了检验模型的可靠性,根据数据点的分布情况,从中选取分布较为分散的10个点作为检核点,其余48个作为模型拟合的数据点。由于测点的平面坐标数值较大,为了避免在运算时出现病态矩阵的情况,需要对测点平面坐标数据进行中心化处理。依据这48个点建立误差方程,求解模型参数并计算检核点中误差。技术路线如图1。

图1 技术路线
首先利用QQPlot分布图和泰森多边形对数据进行探索性分析。从QQPlot分布图(图2)可以看出,样本分位数作出的图形基本在一条直线上。因此,该样本数据的分布近似服从正态分布。粗差点在泰森多边形中表现为众多多边形中颜色与周围截然不同的点。从图3可以看出,没有与周围颜色不一样的多边形,说明泰森多边形代表的样本数据中不含粗差点。
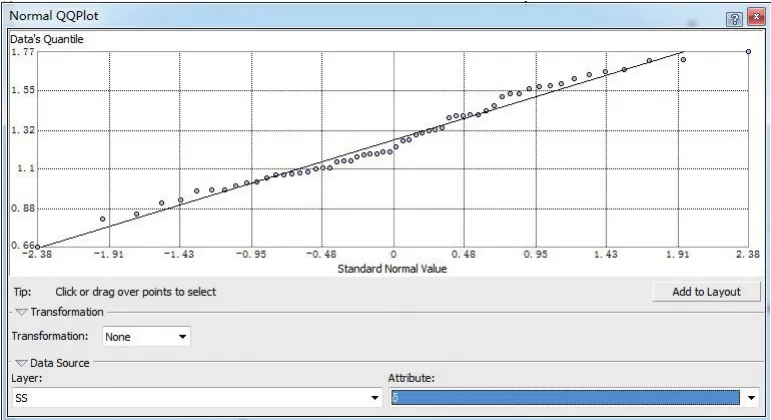
图2 QQPlot分布
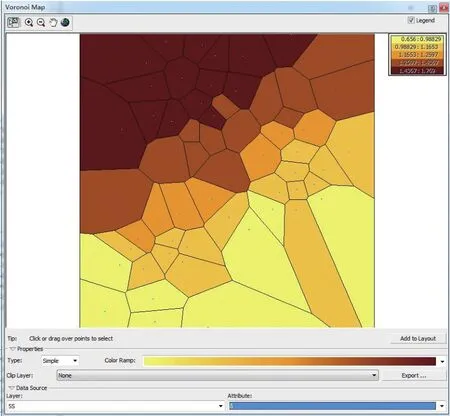
图3 泰森多边形
空间趋势面分析主要依靠样本数据来拟合一个曲面,从而大致反映其空间分布变化情况。图4表明,样本数据在ZX方向和ZY方向呈现二次拟合曲线。
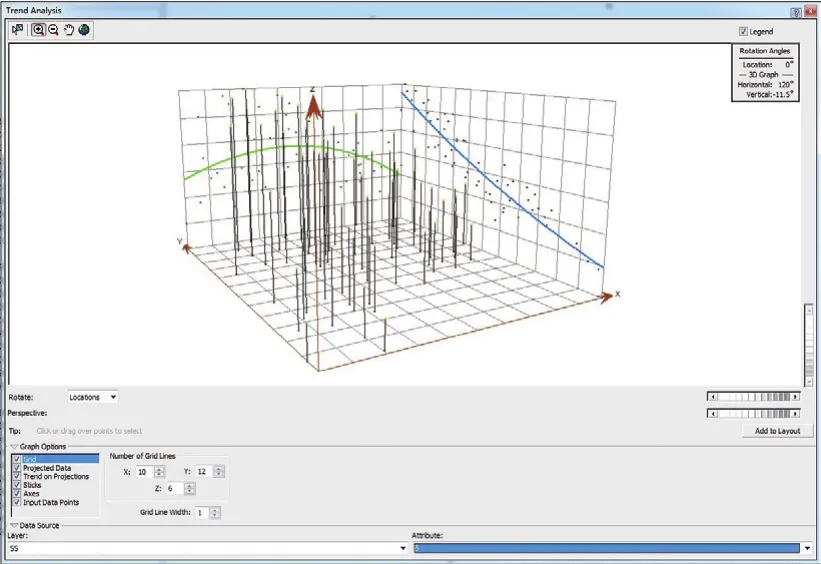
图4 空间趋势面分析
最后,采用地统计分析模块中的插值工具对样本数据进行实验。本实验中采用全局多项式插值、反距离权重和局部多项式插值。每种方法中,参数选取不同会对内插精度产生影响,因此选取的原则是使样本数据通过转换尽可能服从不同算法的前提假设,并使样本数据的空间相关性达到最大,从而使拟合的结果均方根最小。本文开发的加权总体最小二乘趋势面拟合算法工具界面如图5所示。
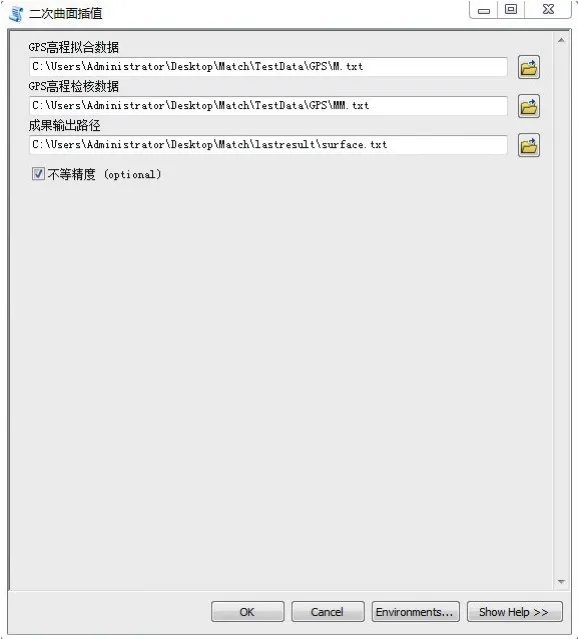
图5 加权总体最小二乘趋势面拟合算法工具界面
地统计分析插值与加权总体最小二乘拟合算法精度对比,如表1所示,其中lb2、gb2、IDW和WTLS分别代表局部多项式、全局多项式、反距离权重和加权总体最小二乘。
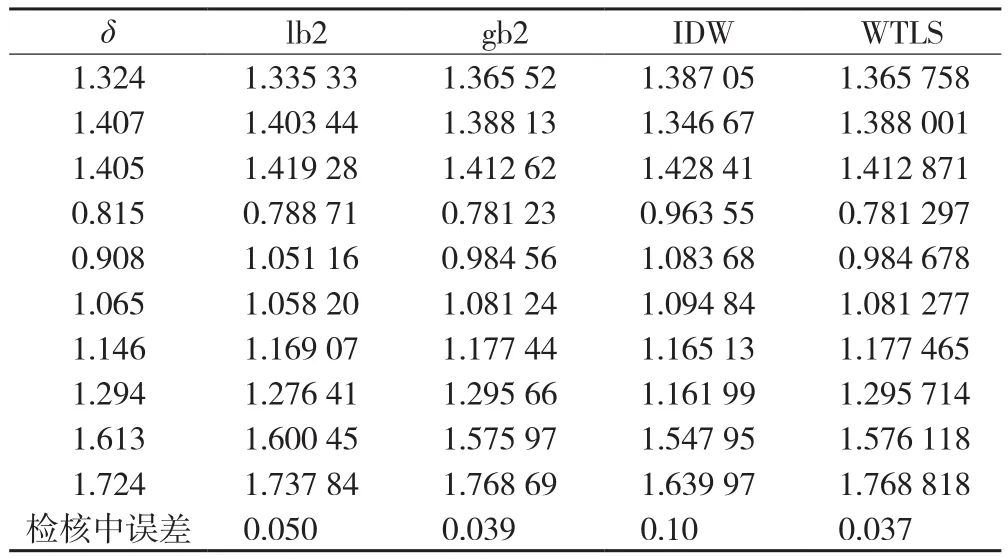
表1 地统计分析插值与加权总体最小二乘拟合算法精度对比
从表1可以看出,WTLS方法的检核中误差较lb2、gb2和IDW有所改善,WTLS方法拟合的精度相比于lb2、gb2和IDW分别提高了26%、5.1%和63%。由此可见,加权总体最小二乘这种顾及系数阵误差和观测值误差,并对不同观测值赋予不同的权值参与平差计算的方法更合理、更精确。
3 结 语
1)当系数阵含有观测随机误差时,应该使用总体最小二乘方法进行参数的求解,而当系数阵列向量之间具有相关性或观测值之间不等权时,就要考虑采用加权总体最小二乘方法。在应用加权总体最小二乘方法时要注意定权方法,确保给定权值的合理性,这样得出的结果才是最优的。
2)以GPS高程异常拟合为例,引入地统计分析工具对空间数据分析和处理,剔除粗差,进行趋势面分析。将确定性插值法的计算结果与加权总体最小二乘算法处理效果比较,为ArcGIS地统计模块的算法设计提供参考。结合开源的Python工具包(NumPy、SciPy),开发基于加权总体最小二乘的趋势面拟合算法,以Python脚本的形式集成到ArcToolbox中,并通过ArcGIS Server发布,脚本简单易用,减少了处理海量数据时人机交互的工作量。
3)曲面拟合是三维建模逆向工程的重要组成部分,主要研究利用空间散乱数据点来重构符合要求的曲面。当空间散乱点具有空间相关性时,就可以采用基于ArcGIS地统计工具的空间插值方法。但是当测量数据精度达不到要求时,拟合后的曲面误差较大。用拟合效果更好的基于加权总体最小二乘的二次曲面建模方法,可以得到更优的曲面拟合精度和更好的未知空间点预测值。
[1] 魏立峰,何建国. GPS高程拟合似大地水准面的方法[J].地理空间信息,2010,8(4): 72-73
[2] 曹先革,刘金鹏.基于MATLAB的GPS高程拟合程序设计[J].地理空间信息,2009,7(2): 22-24
[3] 王小辉,王琪洁,丁元兰,等. 基于二次曲面和BP神经网络组合模型的GPS高程异常拟合[J].大地测量与地球动力学,2012,32(6): 103-105
[4] 王乐洋,许才军.总体最小二乘研究进展[J].武汉大学学报:信息科学版,2013,38(7): 850-856
[5] 张若愚.Python科学计算[M].北京:清华大学出版社,2012
[6] 彭海波,向洪普.基于Python的空间数据批量处理方法[J].测绘与空间地理信息,2011,34(4):81-82
[7] Dobesova Z. Programming Language Python for Data Processing[C].ICECE 2011, 2011
[8] 鲁铁定,周世健.总体最小二乘的迭代解法[J].武汉大学学报:信息科学版,2010,35(11): 1 351-1 354
P216
B
1672-4623(2014)04-0049-03
10.11709/j.issn.1672-4623.2014.04.017
于艳超,硕士,主要研究方向为地理信息系统开发与应用。
2013-10-25。
项目来源:水利部公益性行业科研专项经费资助项目(201201025);国家自然科学基金资助项目(41101374、41101308)。
