空间移动小目标的检测算法

王苗苗，毛晓艳，2，魏春岭，2

(1.北京控制工程研究所，北京 100190;2.空间智能控制技术重点实验室，北京 100190)

O 引言

空间序列图像中的移动小目标(主要指卫星)由于成像距离远，移动速度快，因此在探测器上的成像尺寸小、信噪比较低、机动性不强，缺乏形状纹理特征，且星图中包含大量成像特征与其相似的恒星，无法采用模式识别分类的方法来识别.如何克服恒星及噪声的影响，对空间目标运动轨迹进行精确提取，是当前国内外航天科技领域研究的热点［1］.现有的检测算法主要有先检测后跟踪(DBT，detect before track)算法和检测前跟踪(TBD，track before detect)算法.DBT算法的优点是比较简单，但忽略了目标和背景杂波的时间特性，因此应用范围局限在信噪比较大的情况.TBD算法是把目标分割与后续目标检测合为一步的目标检测方法，如Reed等［2］提出的三维匹配滤波算法、Barniv等［3］提出的动态规划算法以及多级假设检验算法等.理论上具有良好的检测性能，但计算量太大，难以实时实现.针对这一问题，Chu［4］引入了投影变换思想，以损失一定的信噪比为代价大幅度降低算法的计算复杂度.应用投影策略的最典型案例是美国空间中段实验卫星所搭载的可见光相机(SBV)上采用的MTI算法［5］.

本文在对MTI算法仔细研究的基础上，用四邻域二值量化方法优化了MTI中的成对像元二值量化法，采用改进的概率Hough变换算法搜索并确认目标最终轨迹输出结果，相较于原算法中的二阶滤波器，有效减少了候选条痕数目，降低了计算量，节省了存储空间，并且能够检测出移动速度更快的弱小目标以及多个目标，进一步拓展了算法的适用范围.

1 目标成像模型

在一帧图像曝光期间，光子击中CCD像素单元并产生电子.遵从电子数与图像灰度成正比的思路，假设序列图像中像素灰度表示为r(x，y，t).

x=1，2，…，m;y=1，2，…，n;t=1，2，…，N，m，n，N分别为图像的高度、宽度及序列帧数.每个像素对应的灰度值可表示为

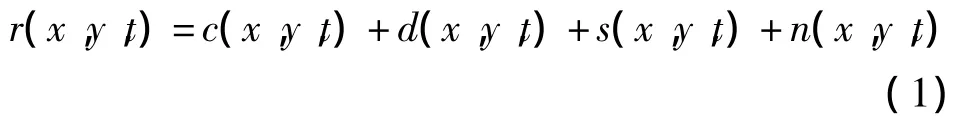
式中，c(x，y，t)为电路引入的高斯噪声，d(x，y，t)为暗电流和背景光照引入的泊松分布噪声，n(x，y，t)是静止目标噪声(恒星、银河、星云状星系)，而s(x，y，t)为待检测目标信号，即移动目标.从统计得出，大多数像素并不是来自于静止目标噪声，因为静止目标相对较少.若不考虑静止目标噪声，那么主要噪声为高斯噪声加泊松噪声，这种加性结合的噪声分布对信号分析来说是相对复杂的.为简化分析，作如下假设:高斯和泊松分布被近似认为是纯高斯的，概率密度函数p(r(x，y，t))如公式(2)所示

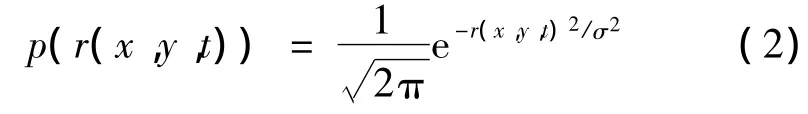
并且泊松分布被近似当作一个常量［5］.另外，本文中移动小目标定义为速度大小≥1像素/帧，方向任意的目标.

2 基于最大值投影的目标检测

2.1 MTI多帧背景抑制算法

MTI算法是一种基于投影变换思想的TBD算法.这一算法首先利用某种数学方法将序列星图从三维时空域有损压缩至二维空间域，得到单一组合帧图像，进而达到抑制背景杂波的目的.对于每一个像元位置 (x，y)，序列样本集 {r(x，y，t)，t=1，2，…，N}将被投影至单个样本z(x，y)，假设只包含噪声的样本是独立同分布的，概率密度为pnoise(r(x，y，t));含有信号的样本也是独立同分布的，其概率密度为psig(r(x，y，t)).引入对数似然比检测的方法则得到最佳投影算子

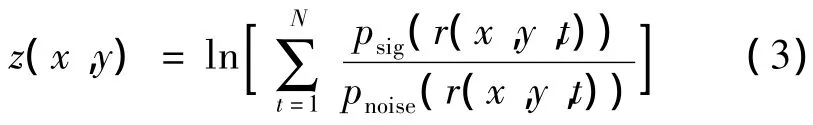
在第一节假设的高斯白噪声模型下，式(3)简化为

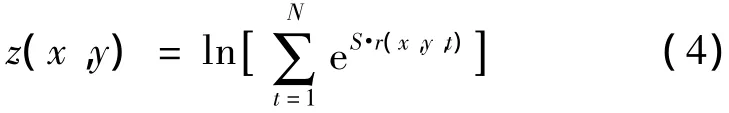
式中S为未投影信号的信噪比.当S较大时，最大的r(x，y，t)支配上式求和，由此得出样本集中最大值就是投影样本的投影算子

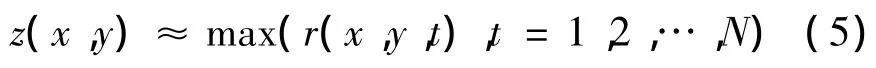
结合传统的假设检验理论构造统计量设计出新的投影算子

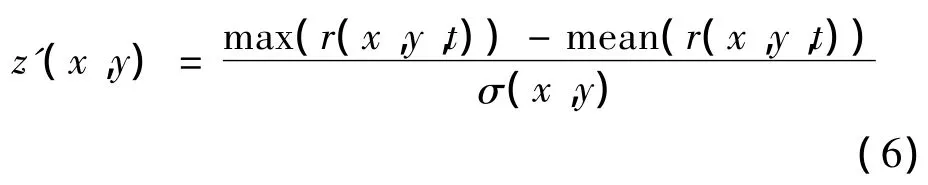
即所有位置上的最大值减去其均值并除以标准差，该式物理含义为目标的峰值信噪比，依据二元信号统计检测原理［6］，信噪比越高的位置出现目标的概率最高.MTI算法以目标的方向特性为依据，对标准化图像进行二元量化

式中，T为阈值，b(x，y)为每个位置对应的点经二值化后的值.上述成对像元量化法相对于传统单点采样二值量化法可使信噪比提高3dB，使得在相同的虚警概率下能够获得更高的检测概率.由于恒星亮度在较长时间内保持不变，对于图像序列而言，该像素点处的均值与最大值基本相等.因此，经二值量化处理得到组合图像帧，保留了移动目标信号，而噪声点被剔除或者大大减少.

2.2 改进的背景抑制算法

MTI算法的成功应用，很大程度上说明了基于最大值投影策略的背景抑制算法的可行性与有效性.但是在对弱小目标的检测方面，上述成对像元二值量化法以目标运动方向特性为依据，并未考虑目标能量分布的特点，因此不能保证目标的完整性.考虑到目标是快速连续运动的，短时间之内可认为是直线运动，当前目标位置的某个邻域内存在能量投影.基于以上分析，本文提出新的二值量化方法.如图1中，当前位置(x，y)周围大小2×2的左上、右上、左下、右下4个邻域的均值分别为

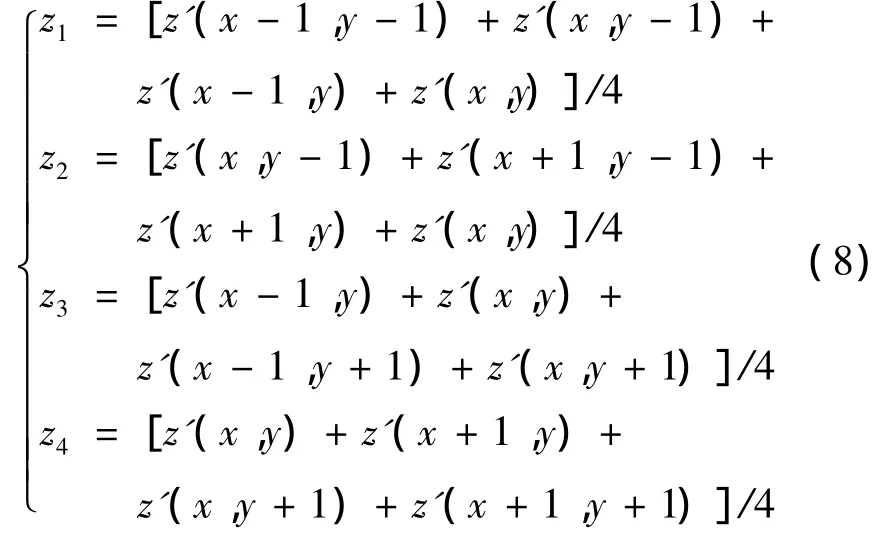
定义四邻域二值量化为

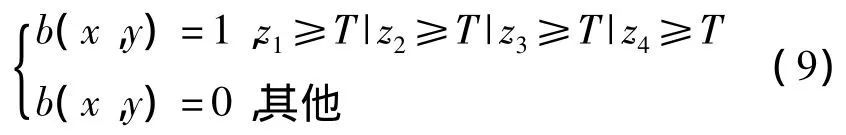
式(9)中，如果四邻域均值中有一个大于T，那么该像素点赋值为“1”，否则为“0”.可以看出，这种方法继承了提高目标信噪比的优点，同时当(x，y)处有目标出现时，采用四个邻域的判断比成对像元二值量化法中四对像元的判断更为有力，能够有效保留目标点的完整，剔除大量的虚警点，这对于后续准确提取目标轨迹至关重要.

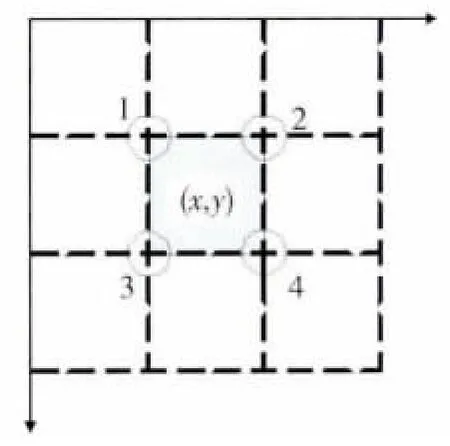
图1 邻域二值化Fig.1 Neighborhood binary

3 目标轨迹提取

3.1 二阶滤波检测器存在的问题

从最大值投影的二值量化图像中提取出目标轨迹，MTI算法采用了由粗检测到精确检测的二阶检测法，即“筛选-确认”二阶匹配滤波器.首先，为了检测出任意角度上的轨迹，通过错切图像使轨迹变为垂直或者水平方向;然后按行或者按列进行速度匹配滤波，若满足阈值条件，则把这条轨迹标记为候选目标条痕;最后，通过能量累积判决从所有候选条痕中提取出目标的真实轨迹.以上方法虽然在一定程度上计算量适中，但是存在以下几个问题:(1)角度搜索时，若旋转的角度过于密集，则计算量大，角度过少时带来的性能损失也不容忽视;(2)筛选阶段逐一搜索，无法优先选择较长轨迹，耗时久，虚假轨迹多，所需存储量大;(3)筛选阶段无法将共线的片段连接在一起，需要在确认阶段调用目标灰度信息进行能量累积判决，计算量大.基于以上问题，有必要对二阶滤波器目标轨迹提取方法进行改进.

3.2 基于改进概率Hough变换的轨迹提取

Hough变换是一种检测、定位直线和解析曲线的有效方法［7］.其基本思想是将图像空间中的检测问题转换到参数空间，通过在参数空间里进行简单的累加统计完成检测任务.由于噪声的随机性，噪声所得到的累积效应很小，故Hough变换能够有效检测直线，同时对噪声具有较强的鲁棒性，可用于低信噪比的目标轨迹检测.实际应用中，检测直线一般采用极坐标直线方程

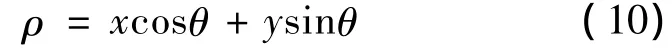
即图像空间的某一点对应参数空间的一条正弦曲线，检测图像空间中的直线需要在参数空间检测正弦曲线的交点.

在以前的研究中，广泛采用的是标准Hough变换直线检测方法.近年来也有一些研究采用了概率Hough变换方法［8］.二者主要区别在于标准Hough变换是在图像空间到参数空间的映射全部完成之后统计各个累加器的计数是否大于累加阈值，从而确定是否存在直线并获得相应直线上的点的集合.而概率Hough变换的映射和直线检测是交替进行的，这样最长直线被最早检测到的概率最大，减少了运算量.考虑到Hough变换的鲁棒性，以及概率Hough变换在计算方面的优越性，分析本文需要解决的问题特点，在传统的概率Hough变换基础上设置了3个阈值，给定一个最小投票数即累加阈值Tv、一个轨迹线最小长度Tl和片段间距最小距离Td，实现目标的真实轨迹提取，具体算法如下:

(1)输入二值化的最大值投影图像，将“1”像元点均加入到未映射的点列表中;

(2)检查未映射点列表是否为空，如果为空，算法结束.否则从列表中随机选取一个点，并将其映射至参数空间，相应的累加器加1;

(3)将已映射的点从列表中移除;

(4)检查参数空间里交点是否达到最小投票数Tv，如果不是，则转向(2);

(5)将该点对应的图像平面上的直线找出来，搜索未映射列表中的点继续累加，延长直线，若该直线不连续，则将距离小于Td的短片段连成线段;

(6)将位于线段上的点从未映射列表中移除;

(7)大于最小长度Tl的线段，删除累加器中这条线段上的点，设置累加器为零，并将该线段添加至输出列表.否则删除累加器中这条线段上的点，设置累加器为零;

(8)转向(2).

以上改进算法实现了直线的粗检测和精检测，即当直线长度累计超过累加阈值时初步确定存在这样一条直线，然后有针对性地去寻找这条直线上的点，如果最后直线总长度累计超过轨迹线总长阈值，则确定这是一条轨迹线，出现直线间断的情况下通过间隔阈值判断确定是否连接.以上方法中，当一条直线被检测出来后，与之相关的点将从列表中消除以使后续的运行过程明显加快，计算复杂度明显降低，能够有效解决MTI算法中的二阶滤波检测器中存在的几个问题.

4 仿真结果与分析

仿真实验在处理器为Intel Core I3－2120，主频3.3GHz，内存为4G的PC机上进行.基于Intel开源计算机视觉库OpenCV和C++编程，在集成开发环境Code::Blocks下开发出了检测程序，对上述算法的有效性和可行性进行了验证.

4.1 二值量化方法的比较验证

用计算机生成10帧420×420的高斯白噪声背景组成的图像序列，在其中添加一个以速度(6，5)像素/帧移动的点目标，亮度设置为10星等.以最大值投影图像作为输入数据，对MTI算法中的成对像元二值量化法和本文提出的四邻域二值量化法进行比较.

图2为原始图像序列中的第8帧，该图包含快速移动的目标卫星，恒星星点以及背景噪声.弱小目标完全淹没在恒星星点以及噪声背景中，难以分辨.图3为最大值投影图像，目标轨迹依稀可见.图4和图5表示对最大值投影图像分别采用成对像元二值化和四领域二值化的结果.不难看出，图5中的噪声点明显少于图4，且目标轨迹更清晰.

图2 原始图像第8帧Fig.2 Input-data frame 8

图3 最大值投影图像Fig.3 Maximum projection

为进一步比较两种方法的性能，将两幅二值图像分别输入MTI算法中的一维速度滤波筛选器中，输出图6和图7所示的目标候选轨迹图像.从两种情况下的滤波结果可以看出，相较于图6的滤波结果，图7的目标点漏检概率为0，虚假轨迹数量明显减少.两种二值化算法的量化比较结果如图8所示:当二值化图像中“1”像元个数为500时，四邻域二值化经滤波后的候选路径比成对像元二值化法少了201条;当“1”像元个数增加到2000个时，候选路径减少了532条.因此，四邻域二值量化法能够更好地保留目标，减少候选路径，大大减少了待处理的数据量，为后续准确提取目标真实轨迹打下了坚实的基础.

4.2 轨迹提取结果及分析

图4 成对二值化Fig.4 Pairwise binary

图5 四邻域二值化Fig.5 Neighborhood binary

图6 滤波结果一Fig.6 Filtered-image1

为检测基于改进概率Hough变换算法的有效性，生成多组图像序列进行仿真实验.在算法的适用性方面，改进算法能够检测出亮度低至10～12星等，移动速度范围高达10～20像素/帧的高速移动弱小目标，对多个小目标的检测也能完成.如图9表示采用改进的概率Hough变换提取出的单目标轨迹.图10为序列图像中含有一个亮度为11星等、移动速度为(6，5)像素/帧的小目标以及另一个亮度为10星等、移动速度为(15，－10)像素/帧的小目标时的轨迹提取结果.

图7 滤波结果二Fig.7 Filtered-image2

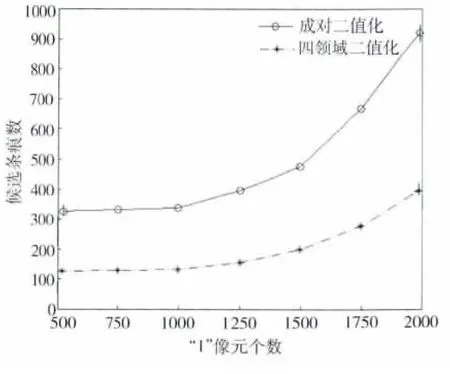
图8 实验结果比较Fig 8 Comparison of experimental results

就算法的计算复杂度而言，MTI算法一维匹配滤波阶段旋转20个角度需要20×420×M(M－1)/2次加法和比较，M为每一列(行)的“1”像元个数，若有n条满足阈值条件的候选路径，则还需要n次能量累积判决，确认最终的轨迹.改进的算法并不需要逐一搜索以及后面的能量累积判决，只需对二值化得到的“1”像元进行投票操作，满足投票阈值的n条候选路径可直接进行长度与间隔判断，因此运算复杂度明显降低.下面是对100组10帧图像序列进行实验后的统计结果，如表1所示.与原算法相比，改进算法的运行时间减少，成功率提高.

图9 单目标轨迹Fig.9 Single target streak

图10 多目标轨迹Fig.10 Multi-targets streaks

表1 MTI算法与改进算法的比较Tab.1 Comparison of improved algorithm and MTI algorithm

5 结束语

本文在MTI算法基础上，基于多帧检测思想提出了改进的算法.主要的研究成果体现在两个方面:一是在目标检测阶段提出了四邻域二值量化方法，较原算法中的成对像元二值量化法能够更好地保持目标的完整性，减少虚警噪声点;二是在轨迹提取阶段采用改进的概率Hough变换法，相比于二阶滤波器能够显著区分真实目标轨迹与虚假条痕，进一步降低了对系统存储空间的要求，运算效率高，适用范围更广.中国在目前理论研究基础上如何设计出各种复杂背景下的弱小目标自适应检测及轨迹提取算法并投入工程应用，仍值得做大量深入的工作.

［1］ 周一宇，李骏，安玮.天基光学空间目标监视信息处理技术分析［J］.光电工程，2008，35(4):43-48.ZHOU Y Y，LI J，AN W.Information processing technology in optical space-based space surveillance［J］.Opto-Electronic Engineering，2008，35(4):43-48.

［2］ REED I S，GAGLIARDI R M，SHAO H M.Application of three-dimensional filtering to moving target detection［J］.IEEE Transactions on Aerospace and Electronic Systems，1983，19(6):898-905.

［3］ BARNIV Y.Dynamic programming solution for detecting dim moving targets［J］.IEEE Transactions on Aerospace and Electronic Systems，1985，21(1):144-156.

［4］ CHU P L.Optimal projection for multidimensional signal detection［J］.IEEE Transactions on Acoustics，Speech and Signal Process，1988，36(5):775-786.

［5］ STOKES G H，VON BRAUN C，SRIDHARAN R，et al.The space-based visible program［J］.Lincoln Laboratory Journal，1999，11(2):205-229.

［6］ 赵树杰.信号检测与估计理论［M］.北京:清华大学出版社，2005:65-146.

［7］ 章毓晋.图像工程［M］.北京:清华大学出版社，2013:184-186.

［8］ MATAS J，GALAMBOS C，KITTLER J.Robust detection of lines using the progressive probabilistic hough transform［J］.Computer Vision and Image Understanding，2000，78(1):119-137.

［9］ 丛明煜，何文家，逯力红，等.复杂背景成像条件下运动点目标的轨迹提取［J］.光学精密工程，2012，20(7):1619-1625.CONG M Y，HE W J，NU L H，et al.Trace extraction of moving point targets in complex background images［J］.Optics and Precision Engineering，2012，20(7):1619-1625.

［10］ 奚晓梁，周晓东，张健.天基监视空间目标轨迹提取算法［J］.电子设计工程，2011，19(19):154-158.XI X L，ZHOU X D，ZHANG J.Image processing algorithm for detection in space-based surveillance ［J］.E-lectronic Design Engineering，2011，19(19):154-158.