露天采场边坡稳定性的有限元数值模拟分析
2014-04-16王昌WANGChang周宗红ZHOUZonghong
王昌 WANG Chang;周宗红 ZHOU Zong-hong
(昆明理工大学国土资源工程学院,昆明 650093)
(Faculty of Land Resource Engineering,Kunming University of Science and Technology,Kunming 650093,China)
0 引言
边坡是由各种不同成因类型、不同地质作用的岩体所组成的复杂介质,又具有类型不同、规模不一、方位各异的地质不连续面,呈现明显的非均匀性和各向异性。在边坡稳定性分析中,有必要掌握其受力状态,分析其应力应变,从而估计边坡的破坏发展,边坡的失稳可能是由局部地区应力达到强度极限,变形增大而逐步发展的。
随着计算机飞速发展,数值计算方法如离散单元法[1-2],刚体一弹簧元法[3],块体单元法[4-6]等方法在边坡稳定性分析中得到了普遍的应用。有限元法能适应各种边界条件和几何形态变化,能考虑岩体的非均质和不连续性,还能考虑非线性应力应变关系,因而它是一种边坡稳定性分析的有用工具。有限元法在边坡领域的应用也越来越广泛[7-8]。本文根据内蒙某金矿露天边坡的工程地质特征,通过有限元软件Phase2建模,利用强度折减法进行边坡稳定性模拟分析,对于露天边坡的灾害防治具有理论和实际意义。
1 边坡稳定性的有限元分析
1.1 岩体力学参数 根据某金矿露天边坡稳定性的1000线工程地质剖面作为分析剖面。根据金矿露天边坡岩体的分布特点,以及拟露天开挖后的情况,本分析考虑了 11 种岩性,即 b1、b2-1、b2-2、b3-1、b3-2、b3-3、b4、h3、花岗岩、中风化层、第四系,其力学性质如表1所示。
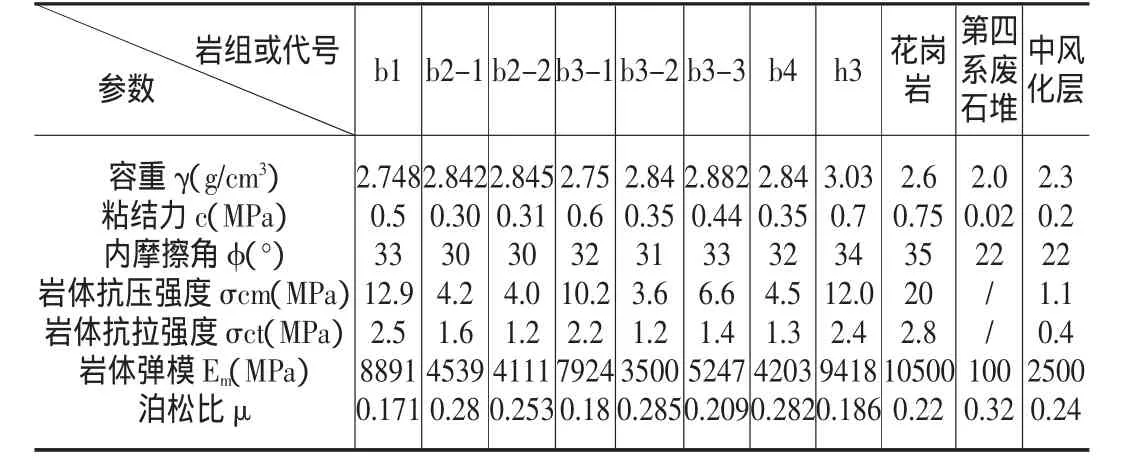
表1 露天采场边坡矿岩力学参数
1.2 计算模型 按照坑底标高1204m,建立B1有限元分模型(模型中左边为南边坡、右边为北边坡,边坡角均为44°,如图1所示),模型边界条件为:坡面为自由面,边坡两侧端面水平方向固定,底部垂直方向固定,原岩应力场为自重应力场。采用最大拉应力判据,结合Mohr-Coulumb屈服准则来确定边坡开挖后的可能出现的拉剪破坏范围,以此来分析浩尧尔忽洞金矿露天边坡的稳定性状况。

图1 B1有限元分模型
1.3 模拟计算结果分析
1.3.1 破坏区分析 B1模型坡体的破坏区主要为拉应力破坏区和剪切破坏区(图2为B1模型的最大剪应变与拉剪破坏区域图)。B1模型拉应力破坏区主要分布在坡顶的第四系和中风化层中,右(南)边坡中少延伸到灰岩(h3)中,最大深度从坡顶开始向下延伸约100m;剪切破坏区主要分布在坡顶的中风化层、灰岩(h3),花岗岩中,最大深度在右(南)边坡灰岩(h3)中,从坡顶开始向下延伸约300m,坡脚也存在少量剪切破坏区。从破坏区分析可知,随着边坡坑底的不断下移,拉应力破坏区和剪切破坏区范围从坡顶不断向坡内延伸,坡面中部逐渐开始出现破坏区。

图2 B1模型的最大剪应变与拉剪破坏区域图
1.3.2 滑动机理分析 图3和图4为B1模型北边坡强度折减法计算安全系数的过程,从强度折减系数F取值为1.19、1.37和1.75情况下的计算出边坡内最大剪应变发展状况来看,可以得出边坡变形破坏的首要部位将为坡脚,其次为坡顶,滑面形状为近似圆弧形,其变形破坏机理为:坡脚剪切破坏区逐步向上发展,坡顶剪切破坏区逐步向坡体内延伸,当坡脚与坡顶的破坏区连通时,边坡产生整体破坏,滑动模式为圆弧滑动。

图3 B1模型北边坡F=1.37时最大剪应变分布图

图4 B1模型北边坡F=1.75时最大剪应变分布
2 结论
①从破坏区分析可知,随着边坡坑底的不断下移,拉应力破坏区和剪切破坏区范围从坡顶不断向坡内延伸,坡面中部逐渐开始出现破坏区。②根据模型北边强度折减法,从强度折减系数F取值为1.37和1.75情况下的计算出边坡内最大剪应变发展状况来看,可以得出边坡变形破坏的首要部位将为坡脚,其次为坡顶,滑面形状为近似圆弧形。③边坡变形破坏机理为:坡脚剪切破坏区逐步向上发展,坡顶剪切破坏区逐步向坡体内延伸,当坡脚与坡顶的破坏区连通时,边坡产生整体破坏,滑动模式为圆弧滑动。
[1]CUNDALL P A.Formulation of three-dimensional distinct element model.part 1.A scheme to detect and represent contacts in system composed of many polyhedral blocks[J].Int.J.Rock Mech.Min.Sci.and Geonechanics Abstracts,1998,25(1)∶10-16.
[2]HART R.CUNDALL P A,LEMOS J.Formulation of threedimensional distinct element model.part 2.mechanical calculations for motion and interaction of a system composed of many polyhedral Blocks [J].Int.J.Rock Mech.Min.Sci.and Geonochanics Abstracts,1988,25(1)∶11-25.
[3]KAWAI T.A new discrete model for analysis of solid mechanics Problem[J].Scisan Kenkyn,1977,29(4):204-207.
[4]CHEN S H,SHAHROUR I,EGGER P,eta1.Analysis ofarch dam abunnent slope using elasto-viscoplustic block theory[J].Rock Mech.and Rock Eng.2002,35(3):1-23.
[5]陈胜宏,汪卫明,邹丽春.岩石边坡开挖及加固分析的弹黏塑性块体元方法[J].岩石力学与工程学报,2002,21(7):953-958.
[6]任青文,余天堂.边坡稳定的块体单元法分析[J].岩石力学与工程学报,2001,20(1):20-24.
[7]郑宏,李春光,李焯芬等.求解安全系数的有限元法[J].岩土工程学报,2002,24(5):323-328.
[8]龚曙光.ANSYS工程应用实例解析[M].北京:机械工业出版社,2003.
