基于功率谱分析的超前预测控制在车载稳定平台中的应用

夏孟龙，李维嘉

（华中科技大学，湖北 武汉430074）

0 引言

车载稳定平台具有隔离载体高频振动的能力，能保持安放在平台上的设备姿态的稳定。常见的陀螺稳定平台，采用的是通过伺服电机驱动平台绕轴线转动的方式，实现平台姿态的稳定。但是陀螺稳定平台的载重量较小，应用范围受到了限制［1］。系统设计了一种单自由度车载稳定平台，采用直线电机作为驱动机构，相比于陀螺稳定平台，具有刚度高、负载大的特点。同时，直线电机还具有结构紧凑、移动速度快、加速度大和定位精度高等优点［2］，能够使平台具有高的响应频率和定位精度，精确补偿车辆行驶时的高频扰动。

1 稳定平台系统的组成

单轴稳定平台的机械结构如图1所示。其中，滑板与底板上分别固定动子与定子，滑板与底板之间通过滑轨支撑，使得滑板能相对底板滑动。推力轴连接在滑板，传递滑板的推力。当推力轴伸出或缩回时，平台通过支撑架绕支撑座摆动，动态补偿外界扰动。液压缓冲器能在滑板超出行程时起到缓冲作用。车载稳定平台控制系统如图2所示。

图1 稳定平台机械结构

图2 稳定平台控制系统硬件组成

2 超前预测控制算法

由于控制系统采用了多环控制的方式，每个内环都要以外环的偏差作为本环的输入值，因此，控制会出现明显的滞后。控制过程中，由于滞后的存在，使得被控量不能及时反映系统所接收的控制信号，引起稳定平台姿态的偏差。图3a为稳定平台的位置闭环相频特性曲线。通过位置闭环相频特性曲线，还可以求得各个频率的理论输入与响应曲线峰－峰值的滞后时间，如图3b所示。从图3b中可以看出，频率在1～7Hz时，峰－峰值滞后时间不断增加，当频率在10Hz以后，虽然滞后相位不断增加，但是峰－峰值的滞后时间基本保持不变。

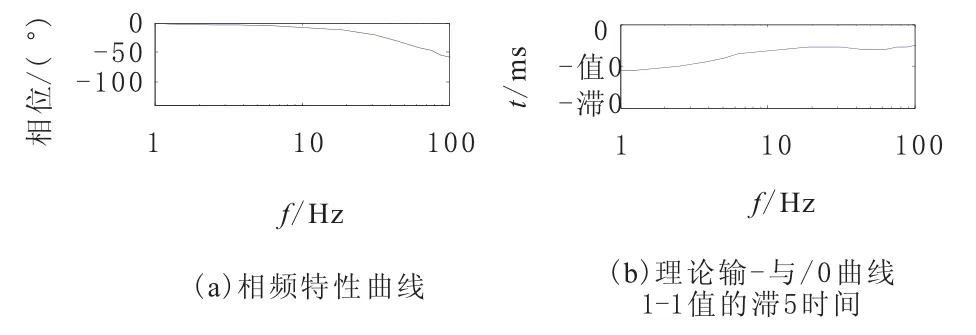
图3 位置闭环的相频特性及与滞后时间

2.1 减小相位滞后的控制方法

减小滞后的控制方法有很多，其中最常用的是PID控制器。PID控制器具有适应性强，调节方便的特点，通过对控制参数进行合理的匹配，在要求不高的情况下，控制精度是可以满足需要的。但是在控制精度要求较高时，PID控制器难以满足要求，必须对其进行改进。

在传递函数的前向通道增加相位超前校正，是常用的一种校正方式。相位超前校正环节在低频段的开环增益很小，对原系统影响很小，但在原系统的开环传递函数穿越频率附近变大，增大了系统带宽，从而提高了系统的响应速度，在高频段，超前校正环节的开环增益为1，保证系统在提高响应速度前提下，稳定性不会降低。通过反馈校正的方式也可以达到减小时间滞后的目的，即在反馈回路上增加微分环节，加强微分作用，达到减小超调量的效果。

以上方法必须事先估计被控系统在扰动下的动态特性，但是，车辆行驶时路况是随机的，无法事先估计扰动情况。然而在一段公路上路面状况又具有一定的统计特性，即在功率谱上各频率波的功率密度比较稳定。因此，可以通过在线功率谱分析的方法，得到一段路程扰动的统计特性，对稳定平台进行补偿。

2.2 基于功率谱分析的超前预测控制

超前预测控制是一种在常规PID控制的基础上增加预测器的方法，它可以有效减小系统的滞后现象。预测控制的基本思想是，预测系统未来的输出状态，以此作为当前时刻的反馈控制信号，即先预测后控制。而常规反馈控制系统是获得当前输出状态，以此作为反馈控制信号。相比之下，超前预测控制可以使系统的输出提前，即减小滞后现象［3－4］。

基于功率谱分析的超前预测控制原理如图4所示。它主要由预测器和功率谱分析器组成。预测器位于姿态控制环的反馈通道，用于接收稳定平台的当前姿态值X（k），通过预测算法得到n步后的预测值Xr（k＋n），将预测值作为姿态控制环的反馈信号。姿态控制环的理论输入信号R（k）＝0（在这里设定稳定平台的期望姿态为水平状态），所以角度误差信号为E（k）＝－Xr（k＋n），E（k）经过位置控制器转换为直线电机的期望位置值，作为直线电机位置闭环的输入信号。功率谱分析器用于采集平台各个时刻的角度值X（1），X（2），…，X（i），通过功率谱分析，得到角度值中各个谐波信号的功率密度分布，估计谐波叠加后的信号对稳定平台滞后时间的影响，从而在线调整预测器的预测步数n，使预测器超前预测的时间能补偿稳定平台的滞后时间。

图4 超前预测控制原理

预测器通过测姿传感器采集平台当前时刻的角度X（k）和角度变化率X′（k），采用三阶阿达姆斯预测算法得到一步预测值为：

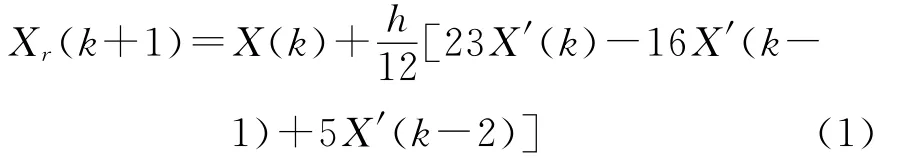
h为采样步长；X′（k），X′（k－1），X′（k－2）为k，k－1，k－2时刻角度变化率。同理，可以得到n步预测值为：

使用n步预测值作为反馈值后，稳定平台的控制时间超前了t＝n·h。

对于稳定平台来讲，其扰动输入是一个满足一定功率谱特性的随机量，可以将其用一系列的正弦信号替代。通过对这一系列正弦信号进行分析，可以得到其对系统滞后的影响，从而确定预测步数n值。此功能由功率谱分析器来实现，功率谱分析器按照一定频率采集平台角度值X（i），并经过快速傅里叶变换（FFT）得到采样信号的频谱特性。在一段实际路面上采集车辆行驶时横摇角度信号，经过快速傅里叶变换得到的功率谱如图5所示。

图5 实际路面信号的功率谱

根据图5的功率谱，可以得到不同频率正弦信号的能量分布情况。功率密度曲线中功率密度的极大值表明，该频率处的正弦波能量集中，对系统响应的滞后起主导作用。随着正弦波频率的增加，功率密度整体呈下降趋势，当功率密度足够小时，对应频率的正弦波对平台的扰动会低于系统分辨率，系统将不对其做出响应，故对滞后的影响可以忽略不计。将这个功率密度阈值（图中横线）与功率密度曲线相交，对于高于阈值的多个极大值，取其中频率的极大值作为影响系统滞后的主要正弦波。根据图3b中频率与时间滞后的关系，可以得到位置闭环的滞后时间。在线改变预测器的预测步数n，使得超前预测时间t＝h·n等于滞后时间，可以有效地补偿位置闭环的滞后现象。

3 实验验证

3.1 计算机模拟平台外界扰动方法

为了模拟平台受到的外界扰动，通过计算机仿真的方法，建立路面不平度时域模型。GB7031－86通过对大量测得的道路随机数据进行处理，基于统计学参数给出了路面平度系数的拟合表达式为：

n为空间频率，单位为m－1；n0为参考空间频率，n0＝0.1m－1；Gq（n0）为参考空间频率n0的路面功率谱密度值，即路面不平度系数，m2／m－1；w为频率指数，决定路面功率谱密度的频率结构。GB7031－86根据路面功率谱密度的差距将路面不平度分为8级，其中E级路面为乡间中等破坏的土路，因此，选用这种恶劣路面进行建模。

采用谐波叠加法产生路面时域模型，谐波叠加法采用以离散谱逼近目标随机过程的模型，是一种离散化数值模拟路面的方法，其理论依据是，随机信号可以通过离散傅里叶变换，分解为一系列具有不同频率和幅值的谐波，谱密度就等于这些谐波幅值的平方［5］。

根据以上方法，使用Matlab仿真平台对E级道路路面建立高度方向时域模型［6］，如图6所示。由于路面高度模型与车辆的横摇角度模型有相关性，因此，对路面高度模型施加一定的比例关系，得到平台的角度扰动模型。

图6 E级路面高度方向时域模型

3.2 试验结果与分析

为了验证PID控制与系统预测控制的效果，通过计算机模拟产生车辆在E级路面上行驶时产生的横摇角度信号，测试平台跟随角度扰动的情况。图7为采用PID控制方法时，得到的输入输出角度值曲线，以及误差的概率密度曲线。

图8为采用超前预测算法后，得到的输入输出角度值曲线，以及误差的概率密度曲线。

图7 PID控制方法试验结果

图8 超前预测控制方法试验结果

4 结束语

设计了一种单自由度稳定平台的控制系统，为了解决控制系统的时滞现象，采用了基于功率谱分析的超前预测控制方法，这种控制方法可以实时地调整预测步数，使超前预测的时间补偿系统的滞后时间。试验结果证明，这种控制方法可以有效减小控制系统的时滞现象，提高了控制精度。

［1］ 杨 浦，李 奇.三轴陀螺稳定平台控制系统设计与实现［J］.中国惯性技术学报，2007，15（2）：171－176.

［2］ 王 利.现代直线电机关键控制技术及应用研究［D］.杭州：浙江大学，2012.

［3］ Liu T H，Lee Y C，Crang Y H.Adaptive controller design for a linear motor control system［J］.IEEE Transactions on Aerospace and Electronic Systems，2004，40（2）：601－616.

［4］ 胡国龙，孙优贤.预测控制进展及其应用研究［J］.电力系统及自动化学报，2003，15（1）：109－114.

［5］ 张永林.车辆道路数据模拟与仿真研究［D］.武汉：华中科技大学，2010.

［6］ 李志强，马吉胜，张亚欧，等.基于 Matlab的路面不平度功率谱计算［J］.兵工自动化，2006，25（3）：77－79.