基于PSR验前信息可信度的Bayes数据融合方法

张宏江， 王树恩， 杜 锋， 姜兆义， 马 威

(1. 装甲兵工程学院装备试用与培训大队，北京 100072； 2. 中国白城兵器试验中心，吉林 白城 137001)

武器系统射击精度是一个最重要的战术技术指标。射击精度包括射击准确度和射击密集度, 前者描述了落点的系统性偏差,后者描述了落点的随机散布特性。随着高新技术广泛应用于弹药系统,弹药的造价越来越高, 单单依靠设计定型的射击试验来评定射击精度，不仅费用高，而且难以得出科学客观的结论。

近年来，Bayes理论发展迅速，文献[1-2]均对Bayes理论进行了比较系统的阐述，这些方法可以融合仿真试验数据，但是存在“数据淹没”问题。文献[3-8]提出了基于验前信息可信度Bayes理论，解决了“数据淹没”问题，但在计算可信度时， 必须在试验之前给出验前概率P(H0)和使用方风险β，这是非常困难的事[1]。鉴于此，本文提出了一种基于相似反映比例(Proportion of Similar Response，PSR)验前信息可信度的Bayes数据融合方法，该方法解决了上述问题，可以用于武器系统射击精度评定试验中。

1 PSR可信度及计算方法

通常，PSR的数量化定义为

(1)

式中：f(x)、g(x)分别为总体分布F(x)、G(x)的概率密度函数。特别地，当F(x)=G(x)时，PSR=1。

PSR刻画了2个总体分布F(x)与G(x)的相似程度，PSR越接近于1,则F(x)与G(x)的差异就越小，当PSR=1时,F(x)与G(x)服从同一分布,这样就可以用PSR作为信息可信度的度量，省去了需要计算β和P(H0)的问题。

式中：

2 融合理论推导

π(θ)=π(μ,D)=π(μ|D)π(D),

其中π(D)为D的验前密度，为逆Gamma分布，即

πi(θ)=πi(μ,D)=πi(μ|D)πi(D)。

正态-逆Gamma分布的参数分别为

π0(μ,D)为现场试验信息的分布函数，它也服从正态-逆Gamma分布，参数为

β0=(n-1)/2，

η0=1/n。

在获得现场试验数据X=(x1,…,xn)之后，利用现场落点数据对验前信息进行PSR检验,得到可信度ci。若认为现场信息是可信的，那么它的可信度c0为1。可信度ci归一化为εi，于是可以得到融合后的验前分布为

式中：

利用Bayes融合公式可以获得(μ,D)的验后分布为

验后分布π(μ,D|X)仍为正态-逆Gamma分布:

加权系数

f(X|πi) =

其中，i=1,2,…,m。

得到π(μ,D|X)后，μ的验后边缘密度为

而D的验后边缘密度为

如果应用平方损失函数， 则μ和D的Bayes估计分别为下列条件期望：

经推导，得出

其中,

3 融合算法计算步骤

通过以上变换，使xi(i=1，2，…，n)具有相同的均值μ0,同时保留了各组试验数据中包含的母体的随机扰动信息εi，可把多组数据合为一组数据。

第2步：应用新的正态分布相容性检验方法检验2个总体的方差和均值的相容性，然后计算PSR，则此种验前信息的可信度为ci=PSRi(i=1,2,…,m)。

第3步：令c0=1，可信度ci(i=1,2,…,m)归一化后得到εi。

第5步：分别计算边缘密度函数值f(X|πi)，求得加权系数λi(i=1,2,…,m)。

第7步：首发命中概率[10]计算公式为

式中：ly、lz为立靶(目标)的尺寸。

4 应用示例

4.1 仿真数据计算结果

假设X～N(29 400,220)，用Matlab随机产生5组数据，每组10发，通过5次程序仿真计算，得到数据εi(i=1,2,…,5)，如表1所示。对比这些数据发现：归一化可信度εi(i=1,2,…,5)均相差不大，并且通过基于PSR可信度的Bayes方法计算，得到均值估计相对误差平均仅有0.05%，方差的估计相对误差平均只有8%，与采用传统的点估计方法得到的均值估计相对误差的平均值0.08%和方差的估计相对误差平均值15%相比均有所降低，说明该方法是有效、合理的。

表1 来自同一母体数据的仿真计算结果

假设X～N(29 400,200)是在设计定型阶段获得的数据，出厂验收试验所获得的数据服从同一个总体X1～N(29 400,200)，用Matlab产生10个设计定型数据和10个出厂验收数据，随机产生仿真数据服从不同分布X2～N(29 200,220)，再随机产生50个仿真数据。

X= (29 645,29 607,29 441,29 368,29 519,

29 287,29 104,29 206,29 822,29 337)，

X1=(29 663,29 416,29 416,29 207,29 317,

29 507,29 251,29 864,29 002,29 467)，

X2=(28 909，29 377，29 038，29 362，28 758，

29 283，29 427，29 199，29 680，29 036，

28 912，29 515，29 553，29 408，29 417，

29 119，29 316，29 228，29 075，28 939，

29 020，29 004，29 218，29 131，29 388，

29 304，29 103，29 166，29 156，28 767，

29 307，29 451，28 627，29 475，29 198，

29 010，29 421，28 962，29 025，28 984，

29 488，29 393，29 100，29 187，29 076，

29 058，28 994，29 445，29 446，29 047)。

经过计算，得到归一化可信度εi(i=1,2,3)分别为0.396 9，0.374 2， 0.229 0，加权系数λi(i=1,2,3)分别为0.542 5，0.452 0， 0.005 5。定型试验经过基于PSR值可信度的Bayes方法估计后，得到均值为29 428，均方差为227，与X均值的真值29 434、X均方差的真值218非常接近，表明仿真数据没有把定型试验数据淹没。

表2为传统Bayes方法与本文方法估计误差对比，可以看出：采用传统Bayes方法估计的方差相对误差达到了26%，导致大量的仿真试验数据淹没了少量的设计定型数据；而采用本文方法得到的均值和方差估计相对误差均远小于传统Bayes方法，不存在数据“淹没”现象。

表2 传统Bayes方法和本文方法估计误差对比

通过仿真计算可以看出：基于PSR值可信度的Bayes方法解决了传统的Bayes方法需要计算β和P(H0)的难题，同时，数据融合结果真实有效，不会出现仿真量大数据“淹没”设计定型数据的问题，因此可以用于射击精度试验。

4.2 实弹射击数据

某型弹定型和正样机数据分别如表3、4所示。

表3 某型弹定型数据

注：指标要求密集度35 cm×35 cm。

表4 某型弹正样机数据

第1步：首先对表3中y方向的3组数据方差进行检验，得到方差检验结果相容；然后对这3组(每组10发)数据的均值进行检验，得到均值检验结果相容，因此，认为这3组数据属于一个整体，可以把这3组数据直接合并为一个大组(即30发数据)。对正样机的2组数据也同样进行上述处理，结果也相容，可以把这2组数据直接合并为一个大组(即20发数据)。z方向也可以进行相应处理，结果一致。

第2步：对这2大组数据进行相容性检验，结果也相容，计算y方向2大组数据的PSR值，得到PSRy=0.970 6，同样计算出PSRz=0.888 2。

第3步：计算y方向归一化可信度，得到ε0=0.507 5，ε1=0.492 5；计算z方向归一化可信度，得到ε0=0.529 6，ε1=0.470 4。

第5步：计算得到y方向边缘密度函数值为1.59×10-6和0.993×10-6,z方向边缘密度函数值为1.492×10-6和0.702×10-6；求得y方向加权系数0.507 5和0.492 5，z方向加权系数0.529 6和0.470 4。

第7步：代入首发命中概率公式，得到

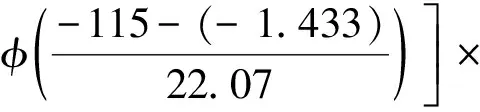
5 结论

本文从实际需求出发，提出了基于PSR验前信息可信度的Bayes数据融合方法，该方法可以融合仿真试验数据、工程样机试验数据，不会出现数据“淹没”现象，并且解决了传统Bayes试验方法需要计算β和P(H0)的难题。仿真结果表明：该方法估计精度高，提高了评定精度，减少了定型试验的样本量。实弹射击结果表明：该方法可以用于突击类武器立靶射击精度试验，能够节约定型试验消耗，缩短定型试验周期，对解决炮弹射击密集度试验和导弹射击精度的定型具有参考价值。

参考文献：

[1] 蔡洪,张士峰,张金槐.Bayes试验分析与评估[M].长沙：国防科技大学出版社, 2004:42-56.

[2] 唐雪梅,张金槐.武器装备小子样试验分析与评估[M].北京:国防工业出版社,2001:15-20.

[3] 朱敏,李红.小子样条件下巡航导弹的命中精度评估方法[J].现代防御技术，2007,35(4):40-43.

[4] 李鹏波,谢红卫,张金槐.考虑验前信息可信度时的Bayes估计[J].国防科技大学学报,2003,25(4):107-110.

[5] 宋笔锋,张延辉.一种综合考虑试验信息和验前信息的系统可靠性分析方法[J].机械强度,1994,16(4):70-72.

[6] 姚志军,王国平,王广伟.验前信息可信度及其在Bayes评估中的应用[J].火力与指挥控制,2007,32(7):51-53.

[7] 刘琦,武小悦.Bayes方法应用中验前信息可信度的影响分析[J].航空计算技术,2010,40(6):1-4.

[8] 王国平.验前信息在射击精度评估中的应用[J].现代防御技术,2006,34 (1):16-18.

[9] 陈卫东,刘旭华,孙逸.同一试验多组数据处理方法研究[J].兵工学报,2007,28(1):42-45.

[10] 郭锡福.远程火炮武器系统射击精度分析[M].北京：国防工业出版社,2004:72-73.