基于云模型和有偏好熵权的装甲装备维修保障能力评估

2014-04-09何成铭韩朝帅

装甲兵工程学院学报 2014年2期

何成铭，张杨，韩朝帅，张龙

(1. 装甲兵工程学院技术保障工程系，北京 100072； 2. 66267部队，河北鹿泉 050026)

装备维修保障工作是一项复杂的系统工程，而装备维修保障能力评估更是装备全系统全寿命管理工作中的重中之重。对装备维修保障能力进行准确的评估，不仅能正确反映维修保障水平的高低，而且对转变保障理念、提高保障人员素质、优化保障力量具有重要的指导意义[1]。在装备维修保障能力评估研究中，常用的方法有神经网络法[2]、层次分析法[3]、模糊综合评判法[4]、突变理论[5]、主成分分析法[6]等，虽然这些方法的应用已经非常成熟，但是在处理系统定性概念时也暴露出了其不能映射随机性特点和准确度不够高的问题。目前，云理论被越来越多地应用于处理系统评价问题，其在解决系统中模型性与随机性关联的问题上体现了较大优越性，可以实现定性与定量之间的互换。近年来，云理论与其他理论方法相结合的研究不断深入，为解决更为复杂的问题提供了有效途径，也拓展了其应用领域。本文围绕装备维修保障能力评估问题，提出了云模型和有偏好熵权相结合的评估方法，可为准确评估装备维修保障能力提供理论支撑。

1 正态云模型和有偏好熵权概述

正态云模型对不确定性概念具有很好的表达能力，可以通过其3个数字特征实现定性概念到定量数据间的转化，相对于传统的处理模糊概念的方法，能够利用更加直观、具体的云图将其呈现出来。有偏好熵权可以综合主客观因素的影响，充分借鉴专家经验，使得评估更具适应性。

1.1 正态云模型基本概念

不同的专家对维修保障能力的评估具有很强的随机性，评估值向评语映射也显现出了不确定性，因此，维修保障能力是极具模糊性的。然而，云模型可以实现定性与定量之间的互换，有效地解决了模糊性与随机性关联的问题。下面给出相关定义[7]。

定义1：设U是一个普通集合U={x}，称为论域，C是论域U上的概念，论域U中的元素x的隶属函数μc(x)∈[0,1]是一有稳定倾向的随机数，称为x对C的隶属度。

定义2：设U为论域，C是论域U上的定性概念，若定量值x∈U，且x是C的一次随机实现，若满足x～(Ex,En′2)，其中En′～N(En,He2)，且对C的确定度满足

(1)

则μc(x)在论域U上的分布称为正态云。式中：Ex、En、He分别为正态云的3个数字特征中的期望、熵和超熵；En′是以En为期望值、He2为方差的正态随机数。

正态云模型是最重要的基本云模型，它是建立在正态分布和正态隶属函数的普遍性基础上的，期望曲线是一个正态型曲线。在正态云的3个数字特征中，Ex代表定性概念在论域中的中心值，En代表一个定性概念可被度量的范围，He表示熵的不确定性，反映了云滴的离散程度。它们在云形中分别反映为云的“最高点”、云的“跨度”和云的“厚度”，图1所示为正态云模型及其数字特征[8]。

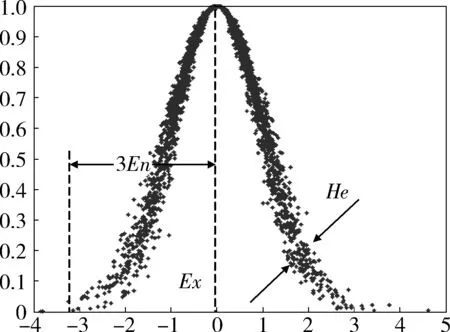
图1 一维正态云模型及其数字特征

云发生器(Cloud Generator, CG)即云生产算法，按功能可分为正向云发生器和逆向云发生器[9]。正向云发生器是输入云的3个数字特征和需要生成的云滴数n，输出每一个云滴的坐标和隶属度，如图2所示；逆向发生器的原理与正向发生器相反，是输入符合某一分布的云滴，输出与之对应的云模型的3个数字特征，如图3所示。

图2 一维正向云发生器

图3 一维逆向云发生器

1.2 有偏好熵权法基本概念

熵权法是一种客观赋权法，就是利用各指标值即指标熵值所包含信息量的大小来确定各指标的权重。有偏好熵权法就是考虑了决策者对各指标有不同的偏好，从而综合了主客观因素的影响，进一步对各指标权重进行修正。假设在某评估决策中有m个方案和n个指标，令第i个方案的第j个指标的值为xij(1≤i≤m,1≤j≤n)，得到初始决策矩阵为X=(xij)m×n。有偏好熵权法的计算步骤如下[10]：

1) 对初始决策矩阵进行标准归一化处理，得到标准矩阵Y=(yij)m×n，其中

(2)

2) 计算得到第j个指标的熵值

(3)

3) 定义第j个指标的差异系数

gj=1-ej；

(4)

4) 计算得到第j个指标的权重

(5)

此处得到各指标的客观权重值W=(w1,w2,…,wn);

5) 综合第j个指标的主观权重λj，修正指标权重为

(6)

2 装甲装备维修保障能力评估指标体系

建立科学合理的装备维修保障能力评估指标体系，是维修保障能力评估研究中最关键的一环，也是能对维修保障能力进行准确评估的基础和依据，它必须能够真实、全面地反映装备维修保障的特点。为了避免出现评估指标重合、不全面等现象，选择维修保障能力评估指标时，需要遵循指标的系统性、完备性、独立性、可操作性、可比性、可测性、动态性、规范性等原则[11]。刘颖等[12]根据上述评估指标体系建立原则，在全面分析系统的基础上，从影响装备维修保障能力的主要因素出发，将其归纳为人力资源、物资资源、信息资源和维修管理等，建立了比较全面的装备维修保障能力评估指标体系，如图4所示。

图4 装甲装备维修保障能力评估指标体系

3 装甲装备维修保障能力评估云模型

3.1 求取各指标的云模型

在评估指标体系中，既有用精确数值描述的定量指标，也有用语言值描述的定性指标，定量指标和定性指标组成的指标集可组成决策矩阵。那么，n个精确数值型表示的一个指标可以用一个云模型来表征[13]。其中：

Ex=(Ex1+Ex2+…+Exn)/n，

(7)

En= max(Ex1+Ex2+…+Exn)/6-

min(Ex1+Ex2+…+Exn)/6。

(8)

n个语言值表示的一个指标也可以用一个一维综合云表示。其中：

Ex= (Ex1En1+Ex2En2+…ExnEnn)/

(Ex1+Ex2+…+Exn)，

(9)

En=En1+En2+…Enn。

(10)

式(7)-(10)中：当指标用精确数值表示时，Ex1,…,Exn为各指标量的值，当指标用语言值表示时，Ex1,…,Exn为指标云模型的期望值；En1,…,Enn为指标云模型的熵。

3.2 求加权综合云的云重心向量

依据云理论，m个指标所反映的系统状态可以用一个m维综合云来表示。这里引入云重心概念，当系统指标发生变化时，该综合云的形状会随之变化，从而表现为云重心的变化[14]。m维综合云的云重心用T表示，

T=(T1,T2,…,Tm)=a×b，

(11)

3.3 计算加权偏离度

(12)

i=1,2,…,m。

将归一化处理后的各指标向量值乘以有偏好熵权值，再相加得到加权偏离度，则偏离度为

(13)

3.4 确定定性评测结果

将评语集中的各级评语值都用云模型来实现，本文采用5个评语组成评语集，即V={强，较强，一般，较弱，弱}，并构成一个定性评测云发生器,如图5所示。针对某一个系统状态，将求得的θ值输入到定性评测云发生器，获得激活云图结果：如果激活某个评语云对象的程度远远大于其他对象，则此评语值为评估结果；如果激活2个评语云对象的程度相差不大，则通过云滴隶属度确定其倾向性。

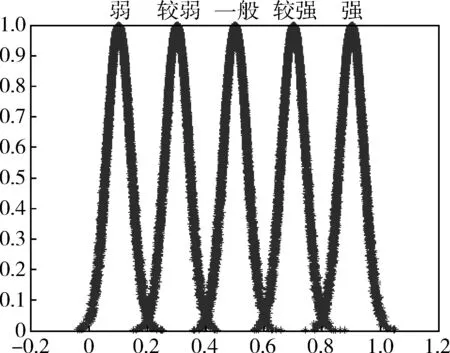
图5 定性评测云发生器

4 示例分析

以某装甲部队维修保障系统为例，采用基于正态云模型和有偏好熵权的方法对其“资源管理”指标进行评估(见图4)，其余指标评估按此方法类推。其具体步骤如下。

1) 计算各指标的云模型。本节以装甲装备维修保障能力评估指标体系中的“资源管理”指标为例，抽取其3个指标进行评判。组成n个专家组对维修管理各因素指标进行评测，得到n种系统状态，选取其中的6种状态为评测样本。由于本实例所选3个指标都是定量指标，因此，不涉及评语量化问题，指标状态见表1。

将表1中的数据按式(7)、(8)求出各指标云模型的期望值和熵，结果见表2。

表1 指标状态表

表2 各指标云模型的期望值和熵

2) 确定各指标的有偏好熵权值。根据式(2)-(5)可求出各指标的客观权重为

W=(w15,w16,w17)=(0.351 7, 0.351 7, 0.296 6)。考虑主观因素，综合专家打分法和AHP法得出各指标主观权重值，由式(6)可得各指标有偏好权重值为

3) 计算加权偏离度。

首先，计算加权综合云的云重心向量为

T= (T15,T16,T17)=(0.79, 0.76, 0.73)×

(0.376 6, 0.376 6, 0.246 8)T=

(0.297 5, 0.286 2, 0.180 2)。

则理想状态下云重心向量为

(0.376 6, 0.376 6, 0.246 8)T=

(0.338 9, 0.346 5, 0.212 2)。

根据式(12)对云重心向量进行归一化处理，得

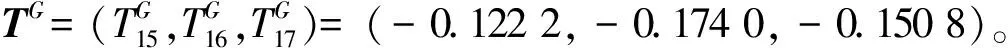
即距离理想状态下的加权偏离度的值为0.138 6，则最终的评估结果为0.861 4。将加权偏离度输入到定性评测云发生器中(如图6所示)，激活了“强”和“较强”2个云对象，而从云滴隶属度来看，其更倾向于“强”。

根据文献[4]中提出的模糊综合评判方法对上述指标数据进行计算，得到的最大评判集指标为0.753 8，与之对应的评估结果为“强”，2种模型评估结果基本一致，验证了该模型可行。模糊综合评判等方法的评估结果更易受数据样本贫乏的影响，且需经过大量矩阵计算，而基于云模型和有偏好熵权的评估方法，则能够经云发生器将样本数据扩大，使结果更加准确，并且通过Matlab等软件实现，计算更加简便。

图6 评测云发生器

5 结论

装甲装备维修保障系统是一个定性与定量、主客观信息综合集成的复杂系统。本文将正态云模型和有偏好熵权相结合，通过云模型实现了定性变量与定量变量之间的精确映射，并且发挥出了定性知识不确定性的优势;有效地综合了主客观因素的影响，特别是充分结合了专家关于装甲装备的宝贵经验，解决了评估中模糊性与随机性并存的问题。示例分析验证了该模型的可行性和准确性。研究表明：由于超熵受经验影响，从而增加了因超熵变化带来的不确定性；同时,该评估模型不能反映出系统的薄弱环节，如何通过评估查找系统薄弱点,是下一步继续研究的重点。

参考文献：

[1] 陈景新,杨辉,吕建新.车辆应急维修保障能力评估指标体系研究[J].武警工程学院学报,2009,25(4):32-33.

[2] 李华，曹晓龙，成江荣.BP神经网络在软件项目风险评估中的应用[J].计算机仿真，2011,28(7):374-378.

[3] 余力，岳振军.基于模糊层次分析法的战役情报效能评估[J].指挥控制与仿真，2011,33(1):58-60.

[4] 马洪文，魏俊，高艳章，等.基于模糊综合评判的装备维修保障系统效能评估[J].兵工自动化，2010,29(7):32-34.

[5] 杨懿，武昌，齐胜利.基于突变理论的维修保障系统效能评估研究[J].空军工程大学学报，2005,6(5):27-32.

[6] 张峰，谢振华，马喜月，等.基于主成分分析的军用飞机维修保障能力评估[J].飞机设计，2011,31(4):76-80.

[7] 龚艳冰，张继国.基于正态云模型和熵权的人口发展现代化程度综合评价[J].资源与环境，2012，22(1)：138-143.

[8] 李德毅，孟海军，史雪梅.隶属云和隶属云发生器[J].计算机研究与发展，1995，32(6)：16-18.

[9] 叶琼，李绍稳，张友华，等.云模型及应用综述[J].计算机工程与设计，2011，32(12)：4198-4201.

[10] 王平，冷宣兵，陈长宇.基于有偏好熵权的维修保障系统效能评估研究[J].舰船电子工程，2008，28(3)：162-164.

[11] 肖丁，陈进军，苏兴，等.装备保障能力评估指标体系研究[J].装备指挥技术学院学报，2011，22(3)：42-45.