LHC能量下的强子多重散射
2014-04-10王宏民
王宏民
(装甲兵工程学院基础部,北京 100072)
研究高能重离子碰撞中带电强子多重散射的赝标快度分布和负二项分布不仅是验证量子色动力学理论的重要途径,而且是了解强子内部结构的重要手段[1]。研究强子多重散射的有效方法之一是色玻璃凝聚理论,这一理论的基础是存在一个饱和标度,通过此标度可以得到偶极散射振幅并抽取未积分胶子分布函数。获取未积分胶子分布函数的途径主要有2种:1) 通过建立唯象模型,目前主要有KLN (Kharzeev Levin Nardi)模型[2]、GBW(Golec-Biernat Wusthoff)模型[3]、CGC(Color Glass Condensate)模型[4]和AdS/CFT (Anti-de Sitter-space/Conformal Field Theory) 模型[5],其中,GBW模型是最早建立起来的胶子饱和模型,AdS/CFT模型建立在非微扰理论基础上,而KLN模型则是最简单的唯象模型;2) 通过求解rcBK(running coupling Balitsky-Kovchegov)或BK演化方程[6]。本文将分别利用唯象模型和rcBK演化方程获取的未积分胶子分布函数研究强子多重散射现象。此外,在计算中笔者还考虑了质子内部结构以及胶子饱和标度与核子半径的依赖关系[7]。
1 计算多重散射的理论模型
根据色玻璃凝聚理论,高能碰撞中强子多重散射截面[8-9]可写为
(1)
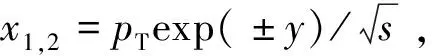
(2)
为跑动耦合常数,其中Λ=ΛQCD=0.2 GeV。
为计算赝标快度(η)分布,需要利用式(3)对式(1)进行相应变换:
(3)
相应的雅可比(Jacobian,J)变换式可写为
(4)

负二项分布是多重散射过程中基本变量之一,获得n个带电粒子的负二项概率[9-10]为
(5)
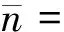
(6)
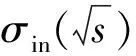
2 未积分胶子分布函数
2.1 利用唯象模型获取未积分胶子分布函数
为了简单而且能说明问题,笔者仍然利用最简单的KLN唯象模型[2,12]来获取未积分胶子分布函数。在KLN模型中,未积分胶子分布函数可以写为
(7)

(8)
参数λ=0.288[3],Tp(r⊥)为质子厚度函数,其采用高斯型分布[13],即
(9)
其中,
(10)
(11)
式中:参数δ=0.8。
2.2 利用rcBK演化方程获取未积分胶子分布函数
rcBK演化方程[6]为
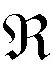
(12)
式中:
N(r,y)-N(r1,y)N(r2,y)],
(13)
为领头阶下的跑动耦合函数,其中,
(14)
为跑动核项,N(r,y)为偶极散射振幅。N(r,y)的初始条件可由唯象模型给出,本文利用GBW唯象模型给出的偶极散射振幅形式[3]:
(15)

rcBK演化方程的未积分胶子分布函数可由偶极散射振幅通过傅里叶变换得到[6,15]:
(16)
式中:J0为第一类零阶贝塞尔函数[16]。
3 计算结果与讨论
3.1 带电粒子赝标快度分布


图1 质子-质子碰撞中带电粒子赝标快度分布曲线
3.2 带电粒子负二项分布


图2 质子-质子碰撞中带电粒子的负二项分布
4 结论
本文在色玻璃凝聚理论框架下,分别利用唯象模型和演化方程得到的未积分胶子分布函数对ALICE和CMS实验数据进行分析,得到如下结论:1)唯象模型中胶子饱和标度对不同质心能量下的质子半径应该存在一定的依赖关系;2)rcBK演化方程在碰撞质心能量较低时不适用。此外,本文理论预言结果有待未来实验验证。
参考文献:
[1] Kumar A, Srivastava P K,Singh B K, et al. Charged Hadron Multiplicity Distribution at Relativistic Heavy Ion Colliders [EB/OL].(2013-10-12)[2013-12-09]. http://aps.arxiv.org/abs/1306.4185
[2] Kharzeev D, Levin E, Nardi M. QCD Saturation and Deuteron-nucleus Collisions [J]. Nucl Phys A, 2004, 730(3/4): 448-459.
[3] Golec-Biernat K,Wusthoff M. Saturation Effects in Deep Inelastic Scattering at Low Q2and its Implications on Diffraction [J]. Phys Rev D, 1999, 59(1): 014017.
[4] Watt G, Kowalski H. Impact Parameter Dependent Color Glass Condensate Dipole Model [J]. Phys Rev D, 2008, 78(1): 014016.
[5] Kovchegov Y V, Lu Z, Rezaeian A H. Comparing AdS/CFT Calculations to HERA F2Data [J]. Phys Rev D, 2009, 80(7): 074023.
[6] Albacete J L, Armesto N, Milhano J G, et al. Nonlinear QCD Meets Data: A Global Analysis of Lepton-Proton Scattering with Running Coupling Balitsky-Kovchegov Evolution [J]. Phys Rev D,2009,80(3):034031.
[7] Armesto N, Salgado C A, Wiedemann U A. Relating High-energy Lepton-hadron, Proton-nucleus and Nucleus-nucleus Collisions Through Geometric Scaling [J]. Phys Rev Lett, 2005, 94(2): 022002.
[8] Kharzeev D, Levin E, Nardi M. Color Glass Condensate at the LHC: Hadron Multiplicities in pp, pA and AA Collisions [J]. Nucl Phys A, 2005, 747(2/4): 609-629.
[9] Dumitru A, Nara Y. KNO Scaling of Fluctuations in pp and pA, and Eccentricities in Heavy-ion Collisions [J]. Phys Rev C, 2012, 85(3): 034907.
[10] Dumitru A, Kharzeev D E, Levin E M, et al. Gluon Saturation in pA Collisions at Energies Available at the CERN Large Hadron Collider: Predictions for Hadron Multiplicities [J]. Phys Rev C, 2012, 85(4): 044920.
[11] 叶其孝,沈永欢. 实用数学手册[M].北京:科学出版社, 2008:656-660.
[12] 王宏民. 高能质子-质子碰撞中的熵密度[J]. 装甲兵工程学院学报,2013,27(5):99-102.
[13] Heinz U, Moreland J S. Energy Dependent Growth of the Nucleon and Hydrodynamic Initial Conditions [J]. Phys Rev C, 2011,84(5): 054905.
[14] Block M M, Halzen F. Forward Hadronic Scattering at 7 TeV: An Update on Predictions for the LHC [J]. Phys Rev D, 2011, 83(7): 077901.
[15] Dumitru A, Hayashigaki A, Jalilian-Marian J. Geometric Scaling Violations in the Central Rapidity Region of d+Au Collisions at RHIC[J]. Nucl Phys A, 2006, 770(1): 57-70.
[16] 杨华军.数学物理方法与计算机仿真[M].北京:电子工业出版社, 2006: 373-375.
[17] Wang H M, Hou Z Y, Zhang B A, et al.J/ψ Production in a GLAUBER Monte Carlo Framework [J]. Int J Mod Phys A, 2010, 25(5): 1009-1018.
[18] CMS Collaboration. Transverse Momentum and Pseudorapidity Distributions of Charged Hadrons in pp Collisions ats1/2=0.9 and 2.36 TeV [J]. JHEP, 2010(2): 041.
[19] CMS Collaboration. Transverse-momentum and Pseudorapidity Distributions of Charged Hadrons in pp Collisions ats1/2=7 TeV [J]. Phys Rev Lett, 2010, 105(2): 022002.
[20] 王宏民,任志明,王洋,等.重离子碰撞中的量子饱和机制[J].装甲兵工程学院学报,2010,24(4):85-87.
[21] ALICE Collaboration. Charged-particle Multiplicity Measurement in Proton-proton Collisions ats1/2= 7 TeV with ALICE at LHC [J]. Eur Phys J C, 2010, 68(3/4): 345-354.
