基于支持向量机的铜基摩擦材料分类判别方法

马润波， 杜建华， 许世蒙， 宫 雷

(1. 装甲兵工程学院基础部，北京 100072； 2. 装甲兵工程学院科研部，北京 100072)

随着军用车辆和工程机械等不断向高速、重载方向发展,对铜基摩擦材料的耐磨性和耐热性提出了更高要求。作为新型铜基摩擦材料研制的理论基础，若能从统计学习理论的角度来研究材料的制备技术，为材料性能的提高提供数学依据，将能为新型材料的研制开拓新的道路。本文针对摩擦材料表面微观形貌图，采用支持向量机方法，对不同配方下铜基摩擦材料的相关结构特征进行统计推断并作出分类，可为进一步研究铜基摩擦材料摩擦层的摩擦生热、疲劳与失效等奠定基础。

1 材料制备与摩擦材料分析

为考察摩擦材料的结构，选取了添加不同质量分数石墨的铜基摩擦材料进行分析，成分配比如表1所示。采用V型混料机混粉2 h，为提高混粉均匀性，可添加1‰的煤油。如采用钟罩炉烧结，摩擦材料的烧结温度定为820 ℃，要求烧结压力20 kg/cm2，烧结材料的密度为4.5 g/cm3。

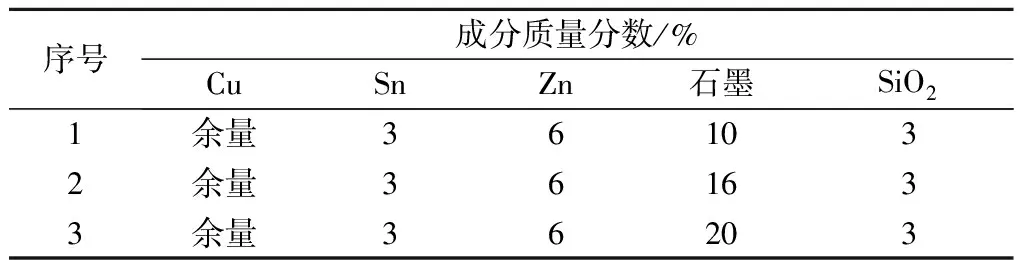
表1 摩擦材料配方

将烧结试样切割磨制后，采用Quanta-200型扫描电子显微镜(SEM)观测铜基复合材料表面微观形貌。图1是添加10%、16%、20%石墨质量分数的铜基摩擦材料表面微观形貌图，其中“黑色”为石墨颗粒，“灰色”为SiO2颗粒，其余为合金。由图1可见：对于不同石墨质量分数的表面微观形貌图，其复杂程度随石墨质量分数的增加而增加，大尺寸石墨颗粒逐渐增多。表2[1]给出了表征石墨颗粒大小的基元[2]长径、短径的数字特征。

图1 添加不同质量分数摩擦材料显微组织相图

表2 石墨颗粒的数字特征

由表2可知：石墨颗粒长径、短径的数学期望和均方差的点估计随其质量分数的增加而不断增大。由方差的统计意义可知石墨颗粒分布逐渐变得集中。

2 学习样本提取

按传统抽样理论，为提高试验评估的准确度，需做大量试验，样本容量越大，精度就越高。但是，由于受到试验条件、试验成本等诸多因素的影响，往往只能做样本容量为n=1或n=2的极小子样试验。因此，极小样本容量的虚拟增广样本方法的应用就显得极为重要。然而，在应用极小样本的虚拟增广方法时，要求试件的分布形式和标准差已知，这对于试件的相关统计特性一无所知的情形，虚拟增广方法就显得无能为力了[3]。支持向量机是基于统计学习理论发展起来的一种新型机器学习算法，能较好地解决小样本问题，当训练样本有限时得到的决策规则，对独立的测试集仍能得到较小误差。

对于石墨颗粒的长径、短径、径心和斜率的分布规律推断，采取“井”字分割方式，按照2种方案分割，如图2所示。

图2 分割方案

方案1：把摩擦材料表面微观形貌图分割为9个正交的子图，分别提取相关的特征指标，对每个子图按照从左至右、从上至下的顺序编号，任意选取其中7个子图作为训练样本，对其分布规律进行统计推断，余下的2个子图作为检验样本，以检验分布规律的可靠性。

方案2：把摩擦材料表面微观形貌图分割为20个正交的子图，分别提取相关的特征指标，对每个子图按照“从左至右、从上至下”的顺序编号，任意选取其中10个子图作为训练样本，余下的10个子图作为检验样本，进行分类判别。

3 摩擦材料表面微观形貌分布规律统计推断

3.1 统计规律分析

对于石墨质量分数为10%、16%和20%的摩擦材料，对图1以分割方案1得到的9张正交子图分别提取石墨的特征指标，即石墨颗粒的长径、短径、径心和斜率，采用科尔莫哥洛夫-斯米尔诺夫方法[4](简称为K-S检验)推断石墨结构特征的分布规律。取检验的显著性水平α=0.05，检验的原假设为

表3中:Z值为K-S检验统计量值;Sig.为检验的显著性概率。对于石墨颗粒的长径和短径，先分别取自然对数，然后再进行非参数假设检验。由表3可知：对于3种石墨质量分数的铜基摩擦材料，均有Sig.>0.05，故可以推断各表面微观形貌图中石墨颗粒的径心和斜率服从正态分布，长径、短径服从对数正态分布。

表3 K-S检验结果

3.2 石墨颗粒统计规律可靠性检验

分别对这3种不同石墨质量分数的铜基摩擦材料表面微观形貌图中石墨颗粒的长径、短径、径心和斜率作检验，原假设为

H01： 石墨颗粒长径的训练样本和检验样

H02：石墨颗粒短径的训练样本和检验样

H03： 石墨颗粒径心的训练样本和检验样

H04：石墨颗粒斜率的训练样本和检验样

由于径心和斜率服从正态分布，长径和短径服从对数正态分布，故对于上述原假设，采用2个独立样本同分布的t检验，检验结果见表4。这里，为便于对比，检验的显著性水平统一取α=0.05。

表4中:F为方差齐性检验统计量值;t为t检验统计量值。由表4可知：在方差齐性检验中，对于3种石墨质量分数的摩擦材料，均有Sig.>0.05，且在均值相等的检验中也均有Sig.>0.05，故可判断训练样本和检验样本中石墨颗粒的斜率、径心、长径和短径均来自同一总体，即可认为3种石墨质量分数的摩擦材料的斜率、径心、长径和短径分布是稳定的，训练样本和检验样本的分布具有可靠性。

4 铜基摩擦材料分类决策

对于分类问题，在相同条件下，虽然获取了大量的数据，但是由于类别不足，无论数据量多大,仍然是小样本数据，传统数据分类算法,如聚类分析、贝叶斯分类算法等，在高精度条件下，由于需要的样本容量较大，所以不能很好地发挥作用。20世纪80年代,Vapnik提出了支持向量机理论，这种方法不直接涉及概率测度和大数定律，具有结构风险最小、可以逼近任意函数且保证全局最优等特点，对小样本、非线性和高维建模等适用性较强，不仅可以避免解析求解的困难，而且可以提高分类的准确性。

根据给定的训练集{(xi,yi),xi∈Rn,yi=-1或1}，寻找实值函数g(x)，用决策函数f(x)=sgn(g(x))推断任一模式x对应的y值，即为分类问题。

由图1可见:铜基摩擦材料表面微观形貌随石墨、合金和二氧化硅等质量分数的变化而变化。表面微观形貌图呈现出的变化，可反映在石墨颗粒的长径、短径、径心横坐标、径心纵坐标、斜率等特征指标的变化上。由于分形维数在一定程度上体现了铜基摩擦材料表面微观形貌的复杂程度[5]，于是，不妨用石墨颗粒的长径、短径、径心横坐标、径心纵坐标、斜率和分形维数等6个指标来刻画铜基摩擦材料。显然，若把石墨基元的6个指标看作随机变量，那么，铜基摩擦材料即可由一个6维随机变量来表示。对于高维随机变量，其分布规律更为复杂，若能降低其维数，将能使分类判别更加简捷、直观。这里，采用主成分分析方法实现了降维，为采用支持向量机方法进行分类判别奠定了基础。

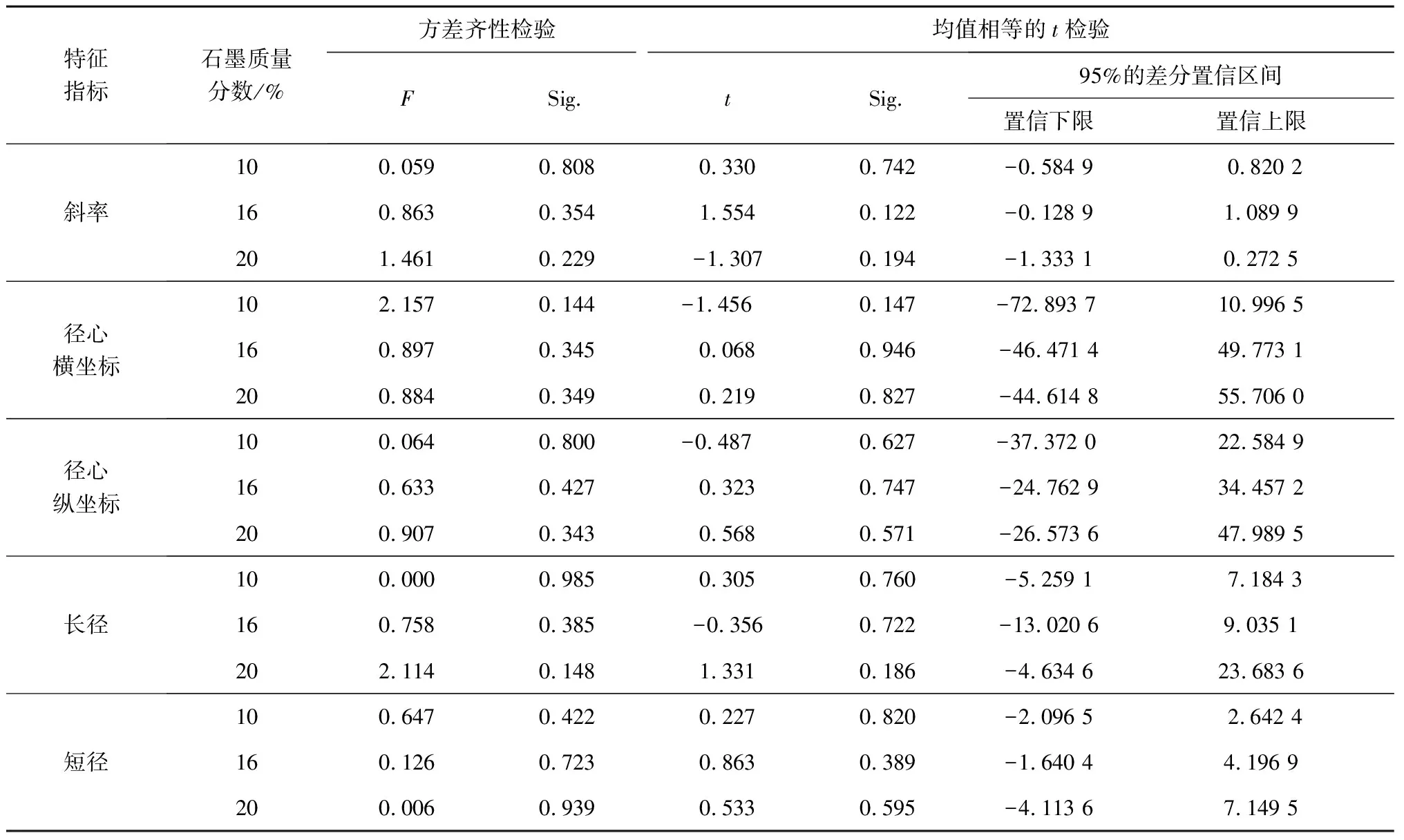
表4 2个独立样本来自同一总体的检验

对于石墨质量分数为10%、16%和20%的摩擦材料，以图1中以分割方案2得到20张正交子图，随机选择10张子图作为训练样本，余下10张子图作为测试样本。对提取的20张子图中石墨基元的6个特征指标，采用主成分分析方法，确定了反映表面微观形貌复杂程度的主要因素，主成分分析结果见表5、6。

由表5可知：前3个主成分的累积贡献率为80.477%，因此取前3个主成分对摩擦材料进行分析即可。由表6可知：第1个主成分对长径、短径和分形维数有绝对值较大的负荷系数；第2个主成分对斜率和径心横坐标有绝对值较大的负荷系数；第3个主成分对径心纵坐标有绝对值较大的负荷系数。于是，第1个主成分可以解释为对表面微观形貌复杂程度的参数；第2个主成分和第3个主成分可以解释为摩擦层中石墨颗粒的位置参数。因此，可把石墨颗粒的长径、短径和分形维数作为分类的依据。

图3给出了3类不同石墨质量分数的摩擦材料关于石墨颗粒的长径、短径和分形维数的散点图。

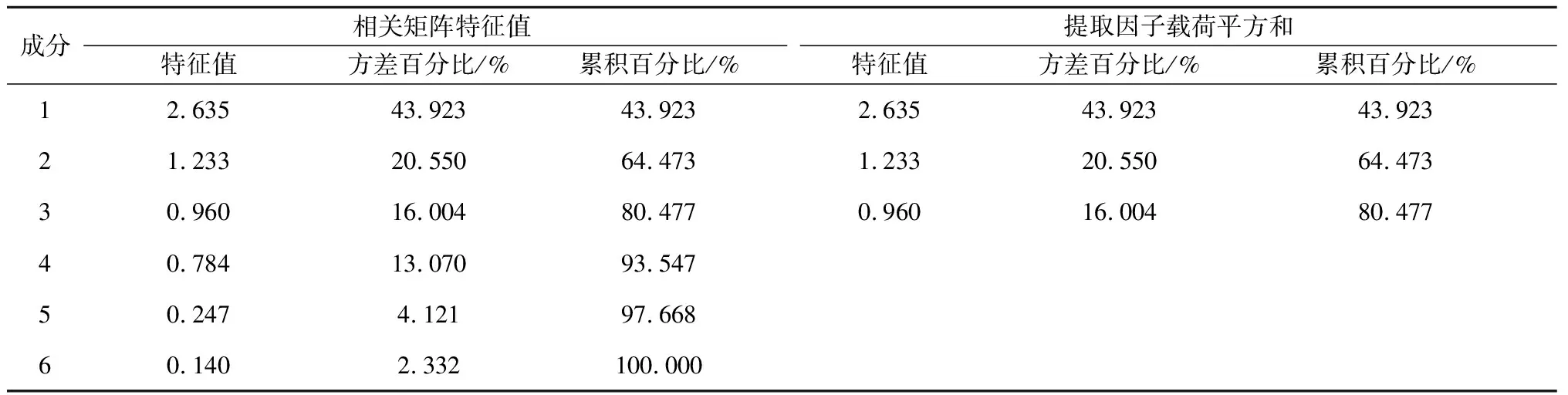
表5 摩擦材料表面微观形貌特征刻画指标的主成分分析

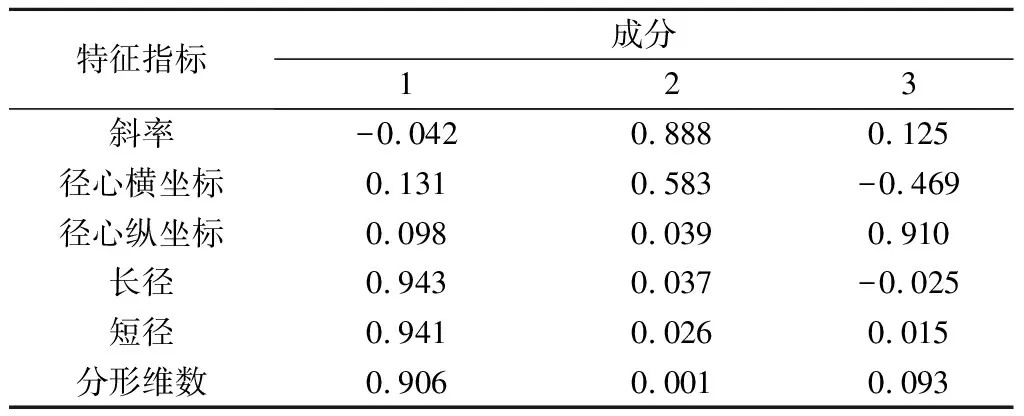
表6 主成分提取结果

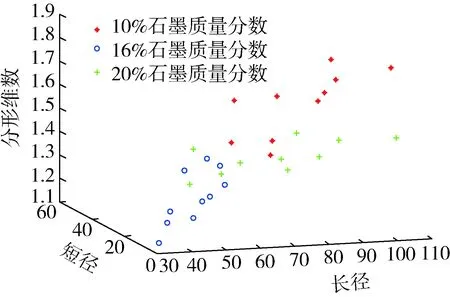
图3 分类散点图

由图3可知：10%和20%石墨质量分数的摩擦材料是线性可分的，16%与10%、20%石墨质量分数的摩擦材料是线性不可分的。为了更加准确地对不同石墨质量分数的摩擦材料进行分类，采用二叉树多分类器[6]的思想对3种不同石墨质量分数的摩擦材料进行分类。分类步骤如下：

1) 将16%石墨质量分数的摩擦材料视为正类，其他2种石墨质量分数的摩擦材料均视为负类；

2) 对10%和20%石墨质量分数的摩擦材料进行分类，分别将二者视为正类和负类；

3) 把石墨颗粒的长径、短径和分形维数3个特征指标作为输入指标，yi为输出指标，yi=-1或1，即若摩擦材料是正类,则yi=1，否则yi=-1(i=1,2,…,n)，把输入指标和输出指标构成一个集合，即为训练集；

4) 对于任意给定的一个输入，根据训练集，寻找实值函数g(x)，以实现分类。

上述训练算法，不仅使所需训练的2类支持向量机的数量减少，而且可提高训练速度和决策速度。由于径向基核函数的优良特性[7]，这里选择径向基核函数作为核函数，分类结果见表7。

表7 分类结果

5 结论

支持向量机方法在摩擦材料的设计、制备和应用中的研究和应用尚不多见。将支持向量机方法与分形理论、主成分分析方法结合一体进行分类判别，既有数据指标的可靠性提升和计算方便的优点，又能与基元模型的指标提取有较好衔接，数据和模型信息利用充分，不失为既能提高精度且可行性、便利性又较强的一类判别分类方法。在应用支持向量机进行铜基摩擦材料分类的研究中，有2个关键问题需要解决：其一，如何构造满足Mercer条件的核函数；其二，对于常用的几个核函数，如高斯核函数中参数如何进行估计及优化等。这些问题的解决，对进一步提高分类的准确率起着重要的作用。

参考文献：

[1] 马润波,许世蒙,杜建华,等.铜基复合材料组织形态分形特征的统计分析与研究[J]. 数学的实践与认识, 2012, 42(7):155-162.

[2] Xu S M, Ma R B, Du J H, et al. The Studies on Basic Element Design of Compound Material Surface Structure Models [J]. Applied Mechanics and Materials Equipment Environmental Engineering, 2013, 365-366(II): 995-998.

[3] 黄玮,冯蕴雯,吕震宙.极小子样试验的虚拟增广样本评估方法[J].西北工业大学学报, 2005,23(3): 384-387.

[4] 王星.非参数统计[M].北京:清华大学出版社,2009.

[5] Chapelle O, Haffner P,Vapnik V N.Support Vector Machines for Histogram-based Image Classification [J].IEEE Transactions on Neural Networks, 1999, 10(5): 1055-1064.

[6] 安金龙,王正欧,马振平.一种新的支持向量机多类分类方法[J].信息与控制,2004,33(3):262-267.

[7] 张小云,刘允才.高斯核支撑向量机的性能分析[J].计算机工程,2003,8(29):22-25.