分区LES/DES混合方法及缝翼三维流场模拟
2014-04-07徐佳敏宋文滨
徐佳敏,宋文滨
(上海交通大学 航空航天学院,上海 200240)
0 引 言
飞机增升装置的设计直接关系到飞机的起飞和着陆场长要求,以及第二阶段爬升率等性能参数,同时越来越高的适航噪声标准逐渐成为飞机气动设计中的重要约束因素。这使得在增升装置设计中越来越需要考虑气动效率指标和噪声特性的多目标优化,缝翼空腔内的复杂流动对于以上两点的影响都至关重要,是主要的研究问题之一[1-3]。深入理解缝翼流场的流动机理对实现高气动效率和低噪声水平的增升装置设计尤为重要,通常需要将数值模拟和实验研究紧密结合[4]。由于前缘缝翼几何外形导致其流场结构非常复杂,涉及很多复杂的物理流动现象,如大范围的低速区域以及主翼前缘可能的高速区域,大压力梯度,强三维展向效应,边界层和尾迹的混合等。这些流动对于准确的数值模拟而言都存在挑战,本文的焦点在于前缘缝翼的非定常流动问题,为了避免襟翼流动对缝翼流场的影响,本文将研究对象限于有限展长的两段翼型。
对机体气动噪声问题中声源信息的数值分析依赖于对压力脉动的准确模拟,可用的数值方法主要包括在定常CFD(Computational Fluid Dynamics)结果上增加声源信息,例如随机噪声产生辐射(Stochastic Noise Generation and Radiation,SNGR)方法[5-6],或者使用非定常方法。常用的非定常方法包括非定常雷诺平 均 (Unsteady Reynolds-Average Navier-Stokes,URANS),大涡模拟(Large Eddy Simulation,LES)方法和脱体涡模拟(Detached Eddy Simulation,DES)方法。非定常雷诺平均仍然是当前工业应用较多的非定常数值模拟方法。基于非定常雷诺平均模型的多段翼型数值模拟已经有了很多相关研究,Jenkins等[7]和 Khorrami等[8]对30P30N 多段翼构型基于非定常雷诺平均方法在不同攻角下进行了计算,与PIV(Particle Image Velocimetry)实验结果进行了对比,并且讨论了缝翼噪声特性随攻角的变化;Khorrami等在用非定常雷诺平均方法捕捉到了有限厚度缝翼尾缘的高频涡脱落[9];König等使用了大涡模拟方法对缝翼流场进行了非定常计算并且将声源提取,再使用声扰动方程(Acoustic Perturbation Equation,APE)方法计算了缝翼噪声的传播特性[10];Ma和Zhang也使用了大涡模拟方法结合声学扰动方程方法对声衬在缝翼上的应用进行了研究[11]。
非定常雷诺平均方法虽然能够用较高的效率得到大致准确的流场,但是由于求解依靠的是基于经验推导的湍流模型,因此其时均特性对小尺度的脉动会产生抑制作用,对流场中细节的小尺度流动特征均无法很好的捕捉;大涡模拟方法虽然能够捕捉到流场中的小尺度的细节流动,但是对于现在的计算机水平而言,高雷诺数下伴随薄边界层所需的巨大网格量对计算资源的要求使得这种方法仍然无法进入实际工程应用。混合方法的发展则能够较好的解决这一矛盾,Imamura等[12]沿弦长方向对整个流域进行了雷诺平均区域以及大涡模拟区域的划分,缝翼空腔以及主翼的前缘均属于大涡模拟区域,因此能够较好的抓住缝翼空腔及其与主翼间隙内细节流动特征,通过频谱分析得到的结果噪声结果也与实验结果比较吻合;法国宇航局(ONERA)的Deck发展了分区脱体涡模拟(Zonal Detached Eddy Simulation,Zonal-DES)方法用于复杂外形的非定常计算[3,13],即自定义脱体涡/雷诺平均计算域的方法来计算三段翼型构型的流场,对缝翼空腔气动噪声预测方面也有很好的表现。对于多段翼型的数值模拟国内也开展了较多的工作,但较少涉及面向气动噪声问题的研究。宋科使用脱体涡模拟方法对带襟翼的多段翼型进行了计算研究工作,但没有涉及缝翼空腔内的复杂流动的细致分析[14];焦予秦同样使用脱体涡模拟方法进行了30P30N多段翼型的非定常计算,但计算局限在二维构型,无法得到三维效应及影响[15];王运涛利用基于雷诺平均方法的高精度数值格式对30P30N多段翼型进行了计算,得到结果与实验符合良好,并且对转捩位置进行了研究[16-17];黄华使用Fluent中脱体涡模拟方法进行了基于前缘射流方法的缝翼噪声控制技术研究[18]。
脱体涡模拟方法在是一种“弱耦合”的混合方法,因为模化的湍流能量与解析的湍流能量之间没有转换机制[19]。该方法主要存在的问题是由于模化应力缺失(Modeled Stress Depletion,MSD)导致的网格诱导分离(Grid Induced Separation,GIS)。Spalart在原脱体涡模拟方法中加入了一个阻尼函数,形成了延迟脱体涡模拟方法(Delayed Detached Eddy Simulation,DDES)较好的解决了网格诱导分离这一非物理现象[20];Deck[3]的分区脱体涡模拟方法通过自定义的湍流作用区域也能很好的克服这一问题。
本文借鉴Deck的分区脱体涡技术的思路,发展了分区LES/DES混合方法,并对典型构型两段翼型缝翼空腔内的三维复杂细节流动及其噪声特性进行了计算分析和讨论。本文结构安排为:第二部分给出了基本流动方程和主要的数值方法;第三部分介绍本文使用的混合方法,计算条件以及计算结果和讨论;第四部分给出主要结论。
1 控制方程和数值方法
1.1 控制方程
在一般曲线坐标系下,无量纲化以后的三维可压缩守恒形式Navier-Stokes方程:
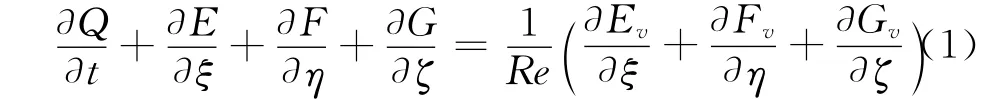
式中,ξ、η、ζ为一般曲线坐标系下三个方向坐标,Q为守恒变量,E、,F、G 为无粘通量,Ev、Fv、Gv为粘性通量,Re为雷诺数。方程通过特征弦长L∞,自由来流密度ρ∞和速度u∞进行无量纲化处理。本文使用基于多块结构化网格的高精度有限差分方法来求解方程(1)。
1.2 空间离散
流场数值计算的空间离散方法主要包括有限差分和有限体积法,在有限差分格式中,与中心差分格式如Jameson中心差分格式[21]相比,迎风格式具有更好的数值稳定性和稳健性。本文使用基于通量差分分裂方法(Finite Difference Splitting,FDS)的 Roe格式,可表述为:
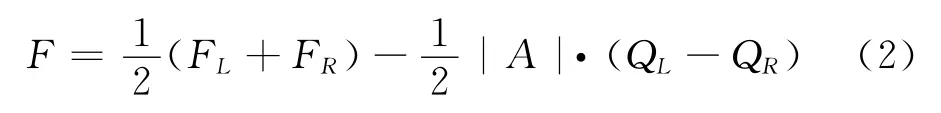
式中,FL和FR分别为控制体表面沿其法向左右两侧的无粘通量矢量,A为采用Roe平均变量计算得到的通量雅可比矩阵,QL和QR分别为控制体表面左右两侧的守恒变量。
空间离散的精度则通过高精度的插值及重构来得到,本文采用的是五阶WENO格式来重构守恒变量QL和QR,其中:

式中,ε的引入是为了避免分母为0的情况发生,ε应当取一个足够小的数。如果ε的取值越大,则离散格式的数值耗散越小[22],由于本文计算工况为低速无激波状态,因此ε可以取稍大值ε=1.3。
1.3 时间推进
本文在时间推进方法上采用基于LU-SGS隐式格式的向后的三点二阶时间推进方法,公式如下。
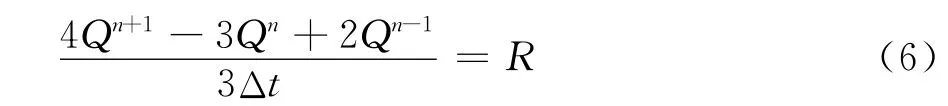
式中,R为方程右端项,Δt为时间步长。隐式LUSGS格式具体方法如下。
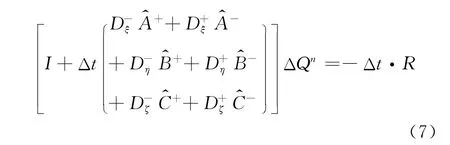

1.4 湍流模拟
基于SA 模型(Spalart-Allmaras Model)的脱体涡数值模拟方法是将SA方程中任意网格节点到最近的物面距离d用~d来表示:

式中,Δ=max(Δx,Δy,Δz),为网格的单元最大尺度;CDES为常数取0.65。
Smagorinsky亚格子应力模型是大涡模拟方法中相对易于实现以及计算高效的亚格子模型,解得湍流涡粘系数:

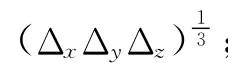
2 基于分区混合方法的数值模拟
2.1 改进的混合方法策略
Deck提出的分区脱体涡方法采用分区指定湍流模型的处理方法,通过在缝翼空腔内使用脱体涡方法进行模拟[3],而在其他区域均使用雷诺平均方法进行处理(图1a),旨在保证能够在所重点关注的缝翼空腔区域内尽可能保证捕捉到非定常流动的细节,同时在流场其余部分使用雷诺平均方法来最大程度上降低计算成本。从图2中的两段翼型熵增云图可以看到,除了缝翼空腔内复杂流动外,来流流过缝翼尾缘与缝翼下表面的加速气流混合产生的尾迹会流过整个主翼弦长,然后随主翼尾迹一起开始耗散,缝翼尾缘产生的尾迹也是缝翼噪声的一个重要组成部分,也是襟缝翼流动相互影响的原因之一。因此在计算能力相对提高的今天,在缝翼空腔内使用大涡模拟方法进行模拟能够帮助更好的来捕捉缝翼空腔内的细节流动,在其余区域均选择脱体涡方法进行计算(图1b)相比之下能够提高缝翼流场一些次要流动细节的捕捉能力,从而提高噪声预测的准确性。在计算特性方面,本文方法对计算网格的要求要高于分区脱体涡方法,尤其在缝翼空腔内,大涡模拟方法对于网格的要求相对于脱体涡方法要更高;在非核心区域的脱体涡网格也需要在有明显非定常流动的区域进行加密,因此也会导致在计算量上相对分区脱体涡方法要更大,但是相比传统的全场大涡模拟方法计算量依旧要小很多。
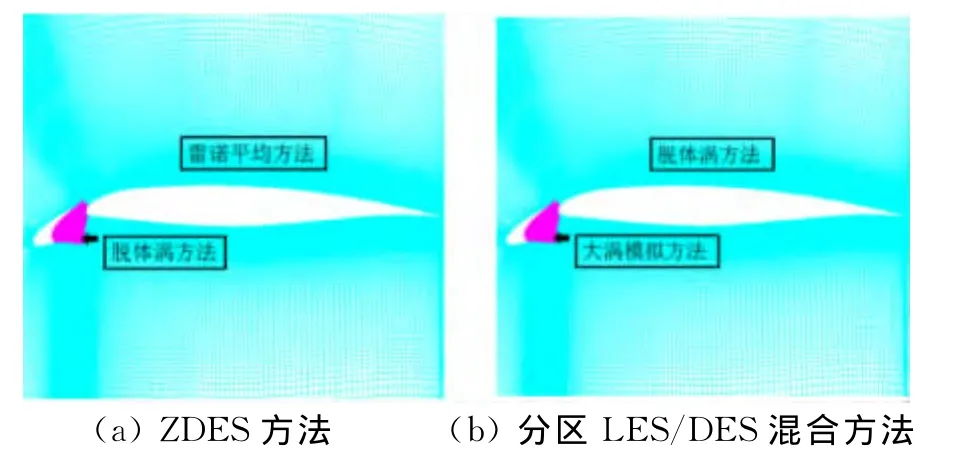
图1 区域混合方法策略Fig.1 Zonal LES/DES method strategy

图2 两段翼型熵增云图Fig.2 Entropycontour of two-element airfoil
由于产生气动噪声的压力脉动的量级远远小于流场平均量的量级,对数值方法计算精度提出很高的要求,因此本文选取的是基于有限差分方法的高精度格式求解,有限体积方法因为其稳定性和鲁棒性而非常适合于复杂外形的计算,但是在高精度计算方面,计算更高效是有限差分方法的优势,特别是在采用高密度网格,针对流动或噪声机理问题开展研究的问题中。
2.2 计算条件与计算网格
本文的研究重点在于前缘缝翼,选择的构型为两段翼型[10],直接选取两段翼型的好处在于可以隔离后缘缝翼对流场特性的影响,突出前缘缝翼的噪声机理。无量纲缝翼弦长为0.15,尾缘厚度为0.0007。计算工况为:自由来流马赫数0.16,攻角13°,基于干净机翼气动弦长(0.4m)以及自由来流速度的雷诺数为1.4×106。
图3给出了计算中采用的计算域和网格分布,其中图3(a)显示整个流域的计算网格;图3(b)给出了两段翼型近场网格拓扑和分布;由于在缝翼空腔内使用的是大涡模拟方法,因此需要尽可能保证此处的网格尺度在各个方向上的一致性(如图3c所示)。有厚度的后缘会产生周期性的涡脱落,是缝翼高频噪声的主要来源,因此缝翼后缘网格需要一定程度上的加密;缝翼的前缘尖端处几何变化很大,从流动角度考虑此处为缝翼下缘加速气流与空腔内低速回流形成的非定常剪切层区域,需要足够好的几何过渡来保证网格变换矩阵的连续性,以此保证此处剪切层区域计算的精确性。展向网格尺度的选取应参考缝翼空腔内的平面网格尺度,尽可能保证缝翼空腔内的网格三个方向尺度一致,考虑到流动的展向效应稍次要与平面内的涡结构捕捉,展向网格尺度选取,共包含21个节点,模型展向无量纲长度0.02,约为缝翼弦长的10%。流域整体网格远场无量纲尺度半径为20,截面网格的网格点为33万,全场网格量约为735万。
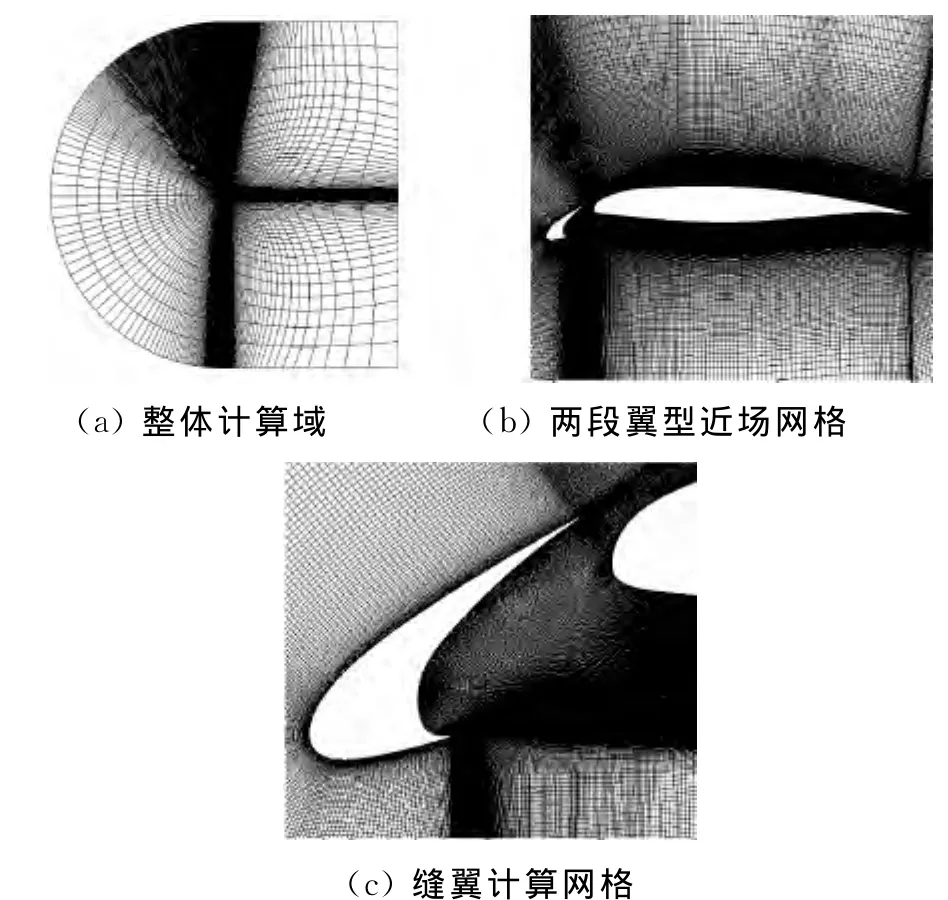
图3 计算网格Fig.3 Computational grid
时间推进采用向后三点二阶精度方法,取无量纲时间步长为0.0005s,从而保证在缝翼空腔内除边界层外其余CFL数均保持在1左右。翼型表面采用无滑移固壁边界条件,展向两端为周期性边界条件,远场采用基于一维黎曼不变量的无反射远场边界条件。
2.3 计算结果与讨论
本节将计算结果和可用的风洞试验数据进行了对比。图4给出了本文计算得到的50%展长位置非定常时间平均压力系数与实验结果对比[10],计算结果与实验吻合良好。图5为缝翼空腔处非定常时间平均马赫数云图,截面A至D的速度剖面(线段的法向速度)与PIV实验的对比如图6所示,两者吻合良好,对本文非定常计算进行了验证。在截面B与C速度剖面的近壁附近因为原试验中PIV粒子数量较少,所以测量可能存在一定误差[10]。图7两段翼型瞬态涡量分布云图,可以清晰的看到计算捕捉到了缝翼后缘尾迹涡量从比较集中的状态发展到离散状态的过程。图8为缝翼空腔内瞬态马赫数分布云图,表明缝翼空腔是一个有很强非定常效应的低速区域,同时可以看到缝翼内侧表面处二次分离的痕迹,二次分离的现象往往与计算模型的展向长度密切相关。图9为缝翼尖端的压力云图,使用高精度的计算格式(图9b)相比低阶格式(图9a)可以更好的捕获到此处的压力脉动脱落的过程。
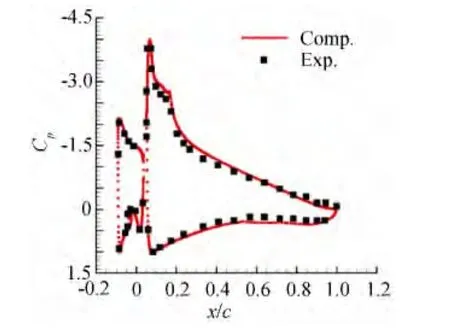
图4 非定常时均压力系数分布Fig.4 Time averaged pressure coefficient distribution
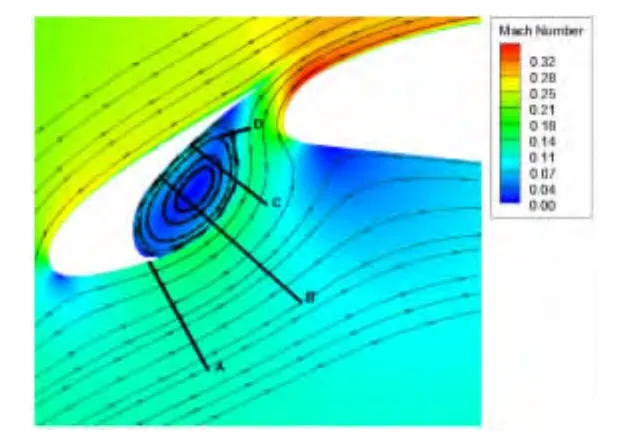
图5 不同速度剖面截面位置分布Fig.5 Velocity profile at different section
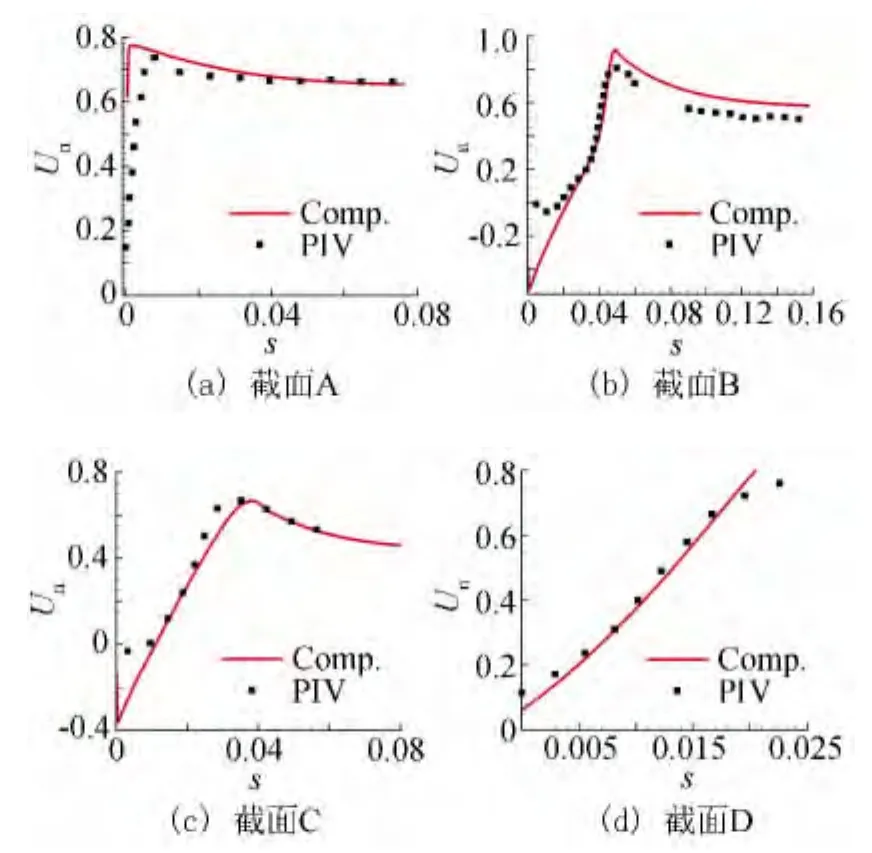
图6 A~D截面位置速度剖面Fig.6 Velocity profile at section A~D

图7 涡量分布云图Fig.7 Contour of vorticity magnitude
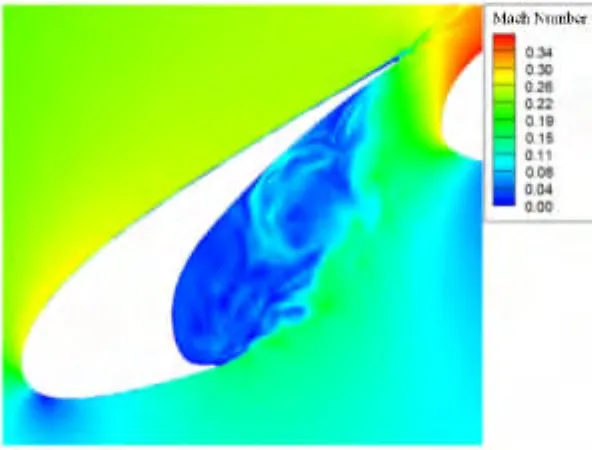
图8 缝翼空腔瞬态马赫数云图(t=0.05s)Fig.8 Mach number contour in slat cove region
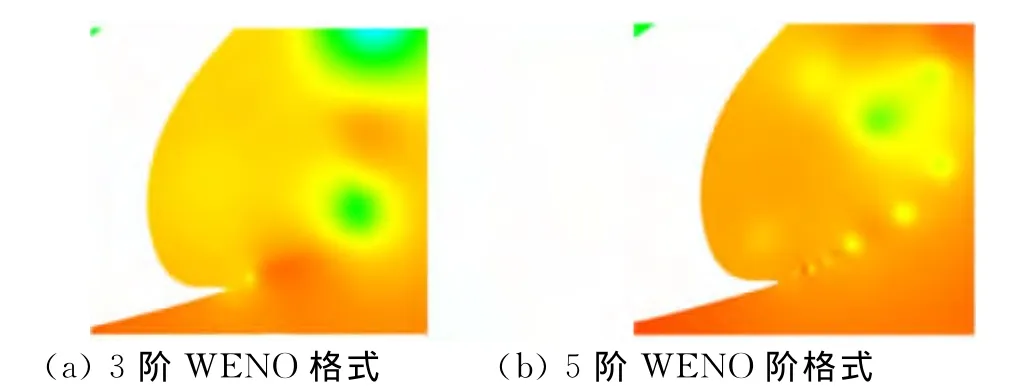
图9 缝翼下缘涡脱落Fig.9 Pressure shedding on the slat cusp
图10为缝翼空腔Q标准等值面图,从图中可以看到在缝翼下缘处剪切层的Kelvin-Helmholtz不稳定性产生的二维展向涡(图10b);展向涡系随剪切层流动发展空间尺度会变大,单位能量尺度变小,但同时也会产生展向效应;涡撞击到缝翼下表面后部分进入回流区,到达缝翼尖端区域,与新生剪切层混合形成一个反馈机制;撞击到缝翼下表面后另一部分的涡沿着缝翼下表面形成一个加速,同时演化为流向涡(图10c),而后与缝翼后缘上表面的加速流混合形成尾迹。
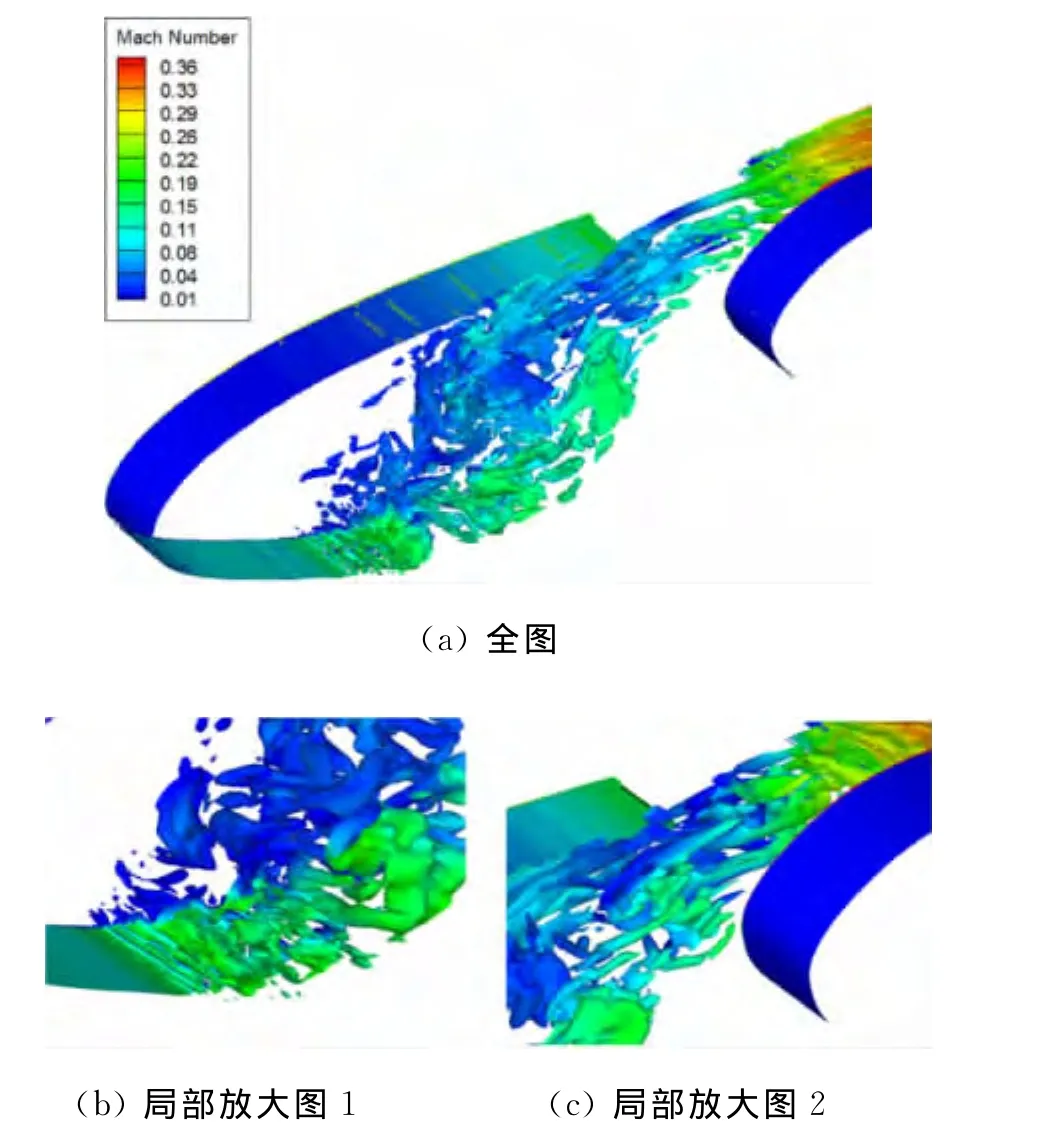
图10 缝翼空腔Q标准等值面图(马赫数云图分布)Fig.10 ISO surface of Q-criterion(contoured with Mach number)
图11中给出缝翼空腔周围设置的压力监测点分布示意图,这些压力监测点分别布置在在缝翼后缘、内壁,以及缝翼空腔内部等感兴趣的位置。图12为缝翼后缘附近的监测点1~3,从频谱上可以非常清晰的看到高频压力脉动的存在,这是由缝翼尾缘上下表面两股加速气流混合带来的高频涡脱落引起的;图14为缝翼空腔右下方的压力监测点9~11的噪声频谱分析图,此处的压力脉动表现出宽频特性,由于监测点11离缝翼尖端距离较近,因此能够看到由于缝翼尖端脱涡引起的高频特性;监测点4~8放置在了整个回流区周围(图13),监测点7和8分布在缝翼尖端产生的强剪切层上,在剪切层中各个尺度的压力脉动能量均比较大,因为流动本身的压力脉动与声场的压力脉动均混合在了一起。监测点7和监测点11一样距离缝翼尖端较近,但是监测点7处于剪切层上,各个频率段的能量都非常大,因此高频段在监测点7没有显得很突出,并且真实情况下缝翼下缘的厚度非常小,因此这种高频效应在真实飞行情况下并不明显。
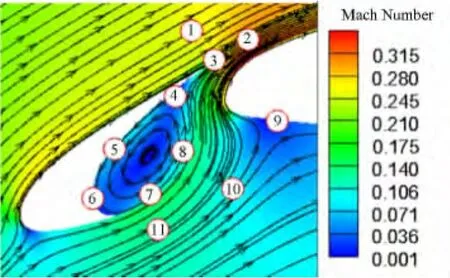
图11 缝翼空腔周围压力监测点分布Fig.11 Pressure observation at points near the slat cove
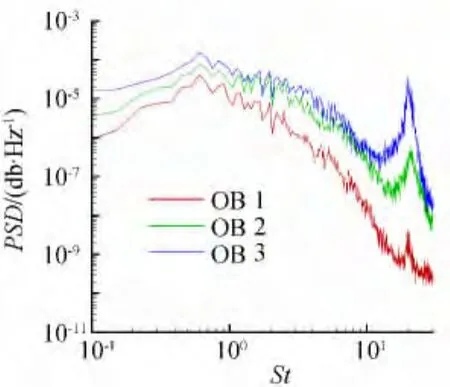
图12 缝翼尾缘压力监测点1~3频谱图Fig.12 Pressure observation points 1~3 near the slat trailing edge
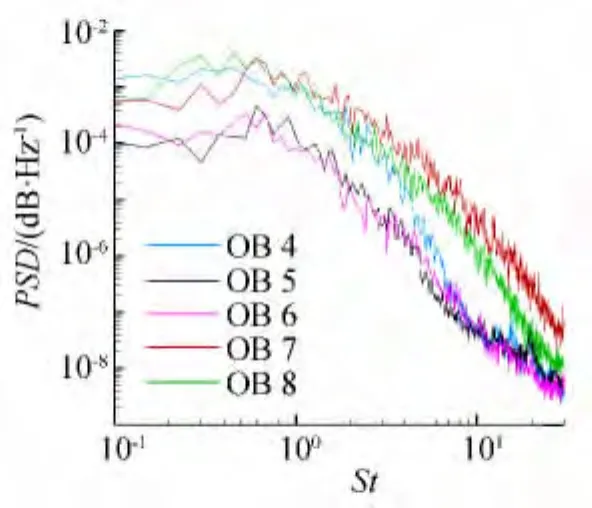
图13 缝翼空腔压力监测点4~8频谱图Fig.13 Pressure observation at points 4~8in the slat cove
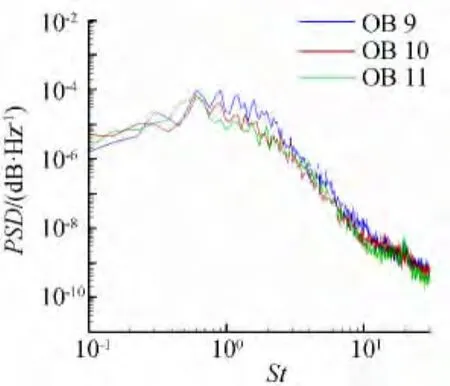
图14 缝翼空腔周围压力监测点9~11频谱图Fig.14 Pressure observation at points 9~11near the slat cove
3 结 论
本文提出一种高精度的分区LES/DES数值模拟方法,并针对有限展长的两段翼型进行数值模拟和分析,在缝翼空腔内的复杂分离流动区域采用大涡模拟方法进行求解,能够明显解决湍流模型对小尺度流动发展的压制作用,进而捕捉到缝翼空腔内流动小尺度流动,以及大能量尺度的涡发展演绎为小能量尺度等细节过程;而在非核心区域内使用脱体涡数值模拟方法相比雷诺平均方法能够更好的捕捉到流场中的缝翼尾迹流动,解得的流场更接近真实物理背景。通过计算结果与已发表实验数据的比较,证实了方法的有效性,最后通过缝翼附近的压力观测点数据对缝翼压力脉动特点进行了分析。
[1]KÖNIG D,KOH S R,SCHRODER W,et al.Slat noise source identification[C].15thAIAA/CEAS Aeroacoustics Conference,May 2009,Miami,AIAA 2009-3100.
[2]AGARWAL A,MORRIS P J.Investigation of the physical mechanisms of tonal sound generation by slats[C].8thAIAA/CEAS Aeroacoustics Conference,June 2002,Breckenridge,AIAA 2002-2575.
[3]DECK S.Zonal-detached-eddy simulation of the flow around a high-lift configuration[J].AIAA Journal,2005,43(11).
[4]张斌,詹浩,朱军.飞机增升装置的数值模拟研究[J].航空工程进展,2011,2(1).
[5]FRANCESCANTONIO P,FERRANTE P,DECONINCK T,et al.Assessment of SNGR method for robust and efficient simulations of flow generated noise[C].19thAIAA/CEAS Aeroacoustics Conference,May 2013,Berlin,AIAA 2013-2264.
[6]YAO H D,DAVIDSON L,ERIKSSON L E,GRUNDESTAM O,et al.Surface integral analogy approaches to computing noise generated by a 3dhigh-lift wing configuration[C].50thAIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition,January 2012,Nashvill,AIAA 2012-0386.
[7]JENKINS L N.,KHORRAMI M R,CHOUDHARI M M.Characterization of unsteady flow structures near leading-edge slat:Part I.PIV measurements[C].10thAIAA/CEAS Aeroacoustics Conference, May 2004, Manchester,AIAA 2004-2801.
[8]KHORRAMI M R,CHOUDHARI M M,JENKINS L N.Characterization of unsteady flow structures near leading-edge slat:Part II.2Dcomputations[C].10thAIAA/CEAS Aeroacoustics Conference,May 2004,Manchester,AIAA 2004-2802.
[9]KHORRAMI M R,BERKMAN M E,CHOUDHARI M M.Unsteady flow computations of a slat with a blunt trailing edge[J].AIAA Journal,2000,38(11):2050-2058.
[10]KÖNIG D,KOH S R,MEINKE M,et al.Two-step simulation of slat noise[J].Computers & Fluids,2010,(39):512-524.
[11]MA Z K,ZHANG X.Numerical investigation of broadband slat noise attenuation with acoustic liner treatment[J].AIAA Journal,2009,47(12).
[12]IMAMURA T,ENOMOTO S,YOKOKAWA Y,et al.Threedimensional unsteady flow computations around a conventional slat of high-lift devices[J].AIAA Journal,2008,46(5):1045-53.
[13]DECK S.Recent improvements in the zonal detached eddy simu-lation(ZDES)formulation[J].Theor.Comput.Fluid Dyn.,2012,26:523-550.
[14]宋科,乔志德.多段翼型大迎角分离流动的DELAYED RANS/LES混合算法[J].航空计算技术,2009,39(3):42-47.
[15]焦予秦,范娟莉,罗淞.多段翼型流动非定常性计算研究[J].科学技术与工程,2011,11(13):2994-2998.
[16]王运涛,王光学,张玉伦.30P-30N多段翼型复杂流场数值模拟技术研究[J].空气动力学学报,2010,28(1):99-103.
[17]王运涛,孟德虹,邓小刚.多段翼型高精度数值模拟技术研究[J].空气动力学学报,2013,31(1):88-93.
[18]黄华.基于前缘射流的缝翼噪声控制研究[D].上海:上海交通大学.2013.
[19]AUPOIX A,ARNAL D,BEZARD H,et al.Transition and turbulence modeling[J].Aerospace Lab.Journal,2011,(2).
[20]SPALART P R,DECK S,SHUR,et al.A new version of detached eddy simulation resistant to ambiguous grid densities[J].Theoretical and Computational Fluid Dynamics,2006,20(3):181-195.
[21]JAMESON A,SCHMIDT W,TURKEL E.Numerical solutions of the Euler equations by finite volume methods using Runge-Kutta time-stepping schemes[C].14thFluid and Plasma Dynamics Conference,1981,California,AIAA 1981-1259.
[22]SHEN Y Q,WANG B Y,ZHA G C.Implicit WENO scheme and high order viscous formulas for compressible flows[C].25thAIAA Applied Aerodynamics Conference,June 2007,Miami,AIAA 2007-4431.
