基于波动期限分解的中国股市风险—回报关系研究

黄祥钟

（福州大学 经济与管理学院，福建 福州 350116）

基于波动期限分解的中国股市风险—回报关系研究

黄祥钟

（福州大学 经济与管理学院，福建 福州 350116）

运用波动期限成分分解方法，在成分GARCH模型的均值方程中，将长期波动成分和短期波动成分分开作为独立的解释变量，从而考察股票价格指数超额收益与长期波动成分及短期波动成分的关系。实证结果显示，短期波动成分对股指回报主要产生负面影响；上证指数的长、短期波动成分对股票收益率的贡献都有显著性，而其他发达市场指数主要受长期波动影响。这表明我国股票市场的风险—回报关系具有特殊性。

期限分解；成分GARCH；风险-回报关系；极大似然法

一、文献综述

金融资产具有风险性和收益性的基本特征，经典的定价理论通常认为二者存在确定的关系（如CAPM模型），但这种关系并不能完全得到实证的支持。Scruggs列出部分学者用不同条件市场方差模型的14个检验结果，其中7个结果显示市场回报与波动率之间的关系无显著性；另外7个有显著性关系的实证结果中，有3个表明回报与波动率的关系是负的[1]。这种风险—回报关系的不确定性与经典理论相悖，学者开始试图通过对风险进行更仔细的刻画以解决这一问题。Adrian和Rosenberg建立两成分波动模型，市场超额回报分别与短期波动成分和长期波动成分相关，因此模型可以衡量不同期限波动对市场超额回报的贡献[2]。Guo和Neely用成分GARCH-均值模型研究了18个国家股票回报与不同期限波动成分的关系，发现其中11个国家的数据回归结果中，长、短期波动成分的系数都有显著性，而且长期波动成分在大部分股市中起到更重要的决定性作用，但系数符号具有不确定性（大部分符号为正）[3]。Zarour和Siriopoulos用类似的方法研究中东地区9个新兴市场的波动成分，发现只有约旦、阿曼和沙特三个市场具有成分结构[4]。这些实证说明不同股票市场上长期风险对股票收益的影响存在差异性和复杂性。Christ offer sent等也把回报的波动分解为长期成分和短期成分，并将其运用于欧式期权的定价[5]。

国内学者对波动分解的研究相对较少。宋逢明和李翰阳将股票收益分解为市场收益和个股收益，从而衡量两个收益的波动，这种分解方法不同于这里提到的波动成分分解方法[6]；张普和吴冲锋通过区分流动性与波动性的差异，对波动性价值进行建模，但文章并没有对波动性的期限成分进行研究[7]。

现有研究表明，波动期限成分分解有助于更好地解释股票指数的风险—回报关系。本文将在成分GARCH模型基础上，将波动的长期成分和短期成分作为独立的解释变量加入均值方程中，从而建立成分GARCH成分均值模型（C-GARCH-CM模型），通过对模型的检验考察两个问题：（1）不同期限的波动成分与股票回报间的关系是否有差异；（2）不同市场的风险—回报关系是否有差异。对这两个问题的考察有助于更深入地理解我国股票市场风险价格的特殊性。

二、波动期限成分分解模型的研究思路

（一）模型思路

标准GARCH模型包括均值方程和方差方程：

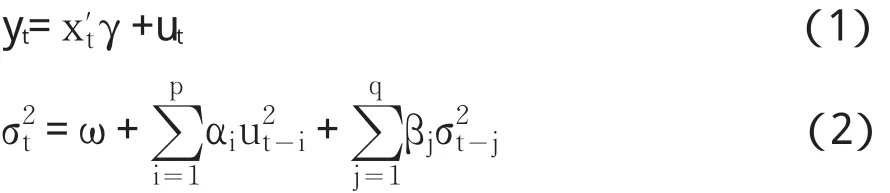
其中公式（1）是均值方程，xt为解释变量的列向量；公式（2）为随机扰动项ut的条件方差方程。根据本文的研究目的，可以将公式（2）的条件方差方程用成分GARCH模型的方差方程代替，从而分解出长期波动成分和短期波动成分，并且将分解出的长、短期波动成分分别作为均值方程的两个解释变量。由此设定成分GARCH成分均值模型（简称为CGARCH-CM模型）如下：

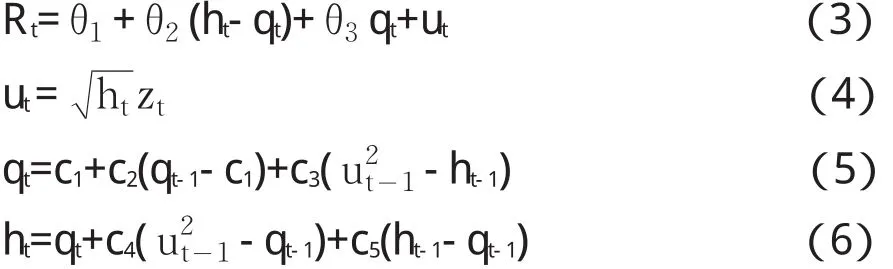
公式（3）是模型的均值方程，Rt表示股票指数的超额回报率，它由qt和ht-qt决定；qt是随时间变化的长期方差（即长期波动成分），它将在c2的作用下缓慢收敛到c1，ht-qt是波动的暂时成分（即短期波动成分）。公式（5）和（6）是成分GARCH模型的基本设定。公式（4）对均值方程中的ut序列施以更强的假定，其中{zt}是一个i.i.d序列，其均值为0，方差为1。根据时间序列的不同分布，可以假设zt序列服从正态分布、t分布或广义误差分布等。这里假设zt服从自由度为k的t分布，自由度k待定。实际运用中，公式（3）中指数超额回报率Rt的计算公式为：

其中rt表示股票指数回报率，rf,t表示相应的无风险利率。rt的计算采用对数收益率，即：

其中Pt和Pt-1分别表示当天和前一个交易日的收盘指数。

（二）模型的计算方法

根据Bollerslev的研究[8]，公式（3）中，如果ut是具有k个自由度、方差为ht的t分布，当k>2时，其密度函数可以写成：

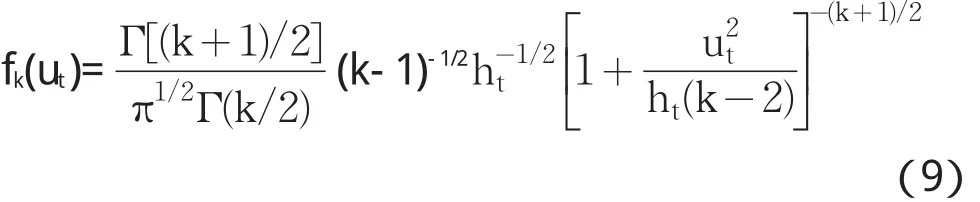
未知参数向量为 ψ =(θ1,θ2,θ3,c1,c2,c3,c4,c5,k)′，此时样本对数似然函数为：

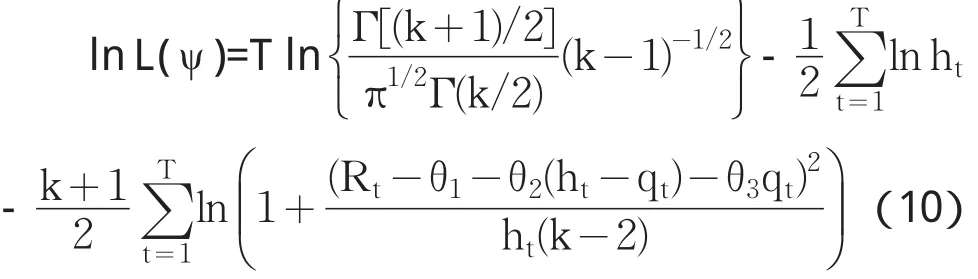
公式（9）和（10）中，Γ(·)代表Gamma函数。针对公式（10）利用极大似然法可求出参数值。本文利用Eviews6.0软件进行统计分析。

三、数据说明

本文主要研究中国股票市场风险—回报关系，同时研究美国、英国和中国香港、中国台湾股票市场的风险—回报关系，从而进行横向对比，以考察中国股票市场风险—回报关系的特殊性。下面说明各市场指数选择、无风险利率选择、时间区间及相应的数据来源。

（一）中国股票市场

上证综合指数是中国最早发布的股票价格指数，是观察中国股票市场走势的重要参考，对中国资本市场上具有举足轻重的影响力，因此选择上证综指作为中国股票市场指数的代表。中国股市从1996年12月16日起实行每日最高波幅限制，实施限制的第一周内（周一至周五）股市波动巨大，其日对数收益率分别为-10.43%、-9.92%、7.15%、-7.50%和-1.92%，之后回复平稳。为避免波幅政策执行初期市场的过度反应对数据分析造成影响，本文选择一周后的1996年12月23日作为开始日期，截止日期为2012年12月31日，这一期间上证综指共有3879个交易日。出于研究时间区间可比性考虑，其他各个市场的时间区间与此处相同。上证综指原始数据来自国泰安数据库CSMAR（若无特别说明，本文其他数据也均来自CSMAR）。

出于数据可得性考虑，本文将7天期银行同业拆借利率作为中国市场的无风险利率，由于同业拆借利率只有月度平均值数据，因此以该值作为当月内每天的无风险利率（用复利方法转化为日利率，以下各市场无风险利率同样处理）。

（二）美国股票市场

标准普尔500（S&P500）指数以加权平均方式计算，涵盖范围广，通常被认为比道·琼斯指数具有更好的代表性，因此本文以其作为美国股票市场指数的代表。与上证综指相同时间区间内，S&P500指数共4041个交易日数据。

美国有发达的国库券市场，美国市场的无风险利率通常选择国库券利率。本文以3个月期国库券贴现利率作为相应交易日的无风险利率，并用复利方法转化为日利率（日度数据，数据来源：美国联邦储备体系网站）。

（三）中国香港股票市场

恒生指数是以发行量为权数的加权平均股价指数，也是香港最具影响力的指数，本文以其作为香港股市指数代表。本文研究期间内，恒生指数交易日共3967个。

1991年以后，香港政府就没有发行过政府债券；由于“非典”等因素的影响，2004年发行过一次政府债券，之后到2009年才较为连续地发行。学者研究香港市场情况时，一般无法使用政府债券利率作为无风险利率，而只能使用其他利率代替。考虑到联系汇率制下港元与美元的密切关联，本文选择3个月美国国库券利率作为香港市场的无风险利率。

（四）英国股票市场

伦敦金融时报100指数（FTSE100），又称富时100指数，是在伦敦证券交易所上市的最大的100家公司的股票价格指数，它是欧洲最主要的股价指数之一，本文以此作为英国股市指数的代表。本文研究期间内，FTSE100指数交易日共4045个。

英国是最早发行国库券的国家，国库券收益率是常用的无风险利率，本文用3个月期英国国库券月度平均贴现率作为英国股票市场的无风险利率（月度数据，数据来源：英格兰银行网站）。

（五）中国台湾股票市场

台湾加权指数（TAIEX）是中国台湾地区最重要的股票指数，其计算方法与S&P500相同，能够反映整体市场股票价值变动，本文采用其作为台湾股市指数代表。研究期间台湾加权指数共3997个交易日。

台湾当局发行债券数量有限，无法用债券利率作为无风险利率。本文选择台湾五大行①包括台湾银行、土地银行、合作金库、第一商银、华南银行和彰化银行。其中不同时间土地银行和彰化银行只用其中一家数据。3个月定期存款平均利率为无风险利率（月度数据，数据来源：台湾货币当局网站），由于该网站能够获得的存款利率数据最早为2001年1月，因此1996年12月至2000年12月的存款利率数据以台湾银行公布的3个月期定期存款利率代替(月度数据，数据来源：台湾银行网站)。

四、实证结果

（一）数据描述性统计结果

表1给出各指数超额收益率数据的描述性统计结果：

从表1中各数据的偏度和峰度值来看，数据序列都不符合正态分布基本特征，而且各序列的J-B统计量的概率值均为0，因此不能认为样本服从正态分布。观察QQ图可知（因篇幅关系，这里不给出具体图形），此处各指数样本的分布更接近t分布，下面都以t分布假设下的极大似然函数公式（10）计算C-GARCH-CM模型的参数。

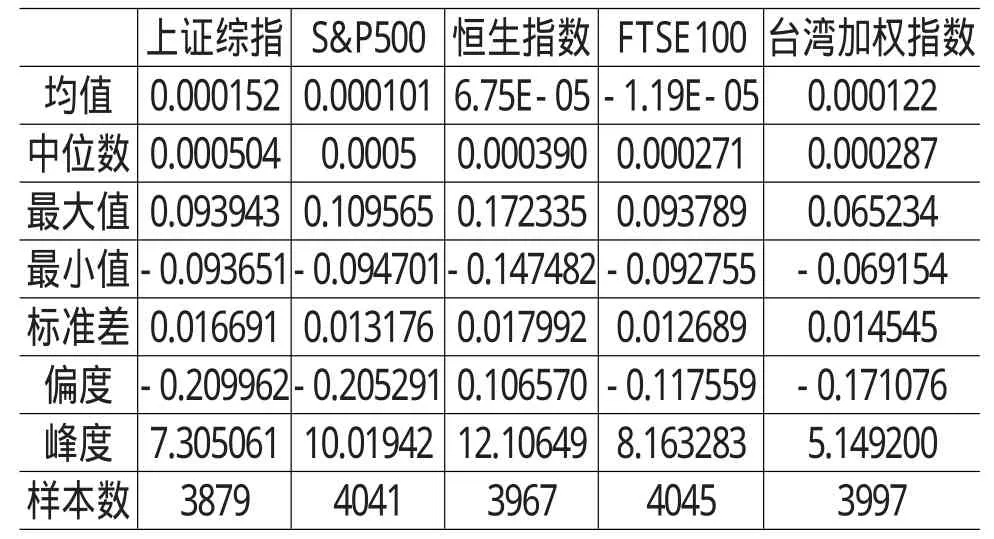
表1 指数超额收益率数据的描述性统计

（二）模型计算结果

根据公式（3）至公式（10），在Eviews中计算各个市场指数的C-GARCH-CM模型，计算结果见表2。

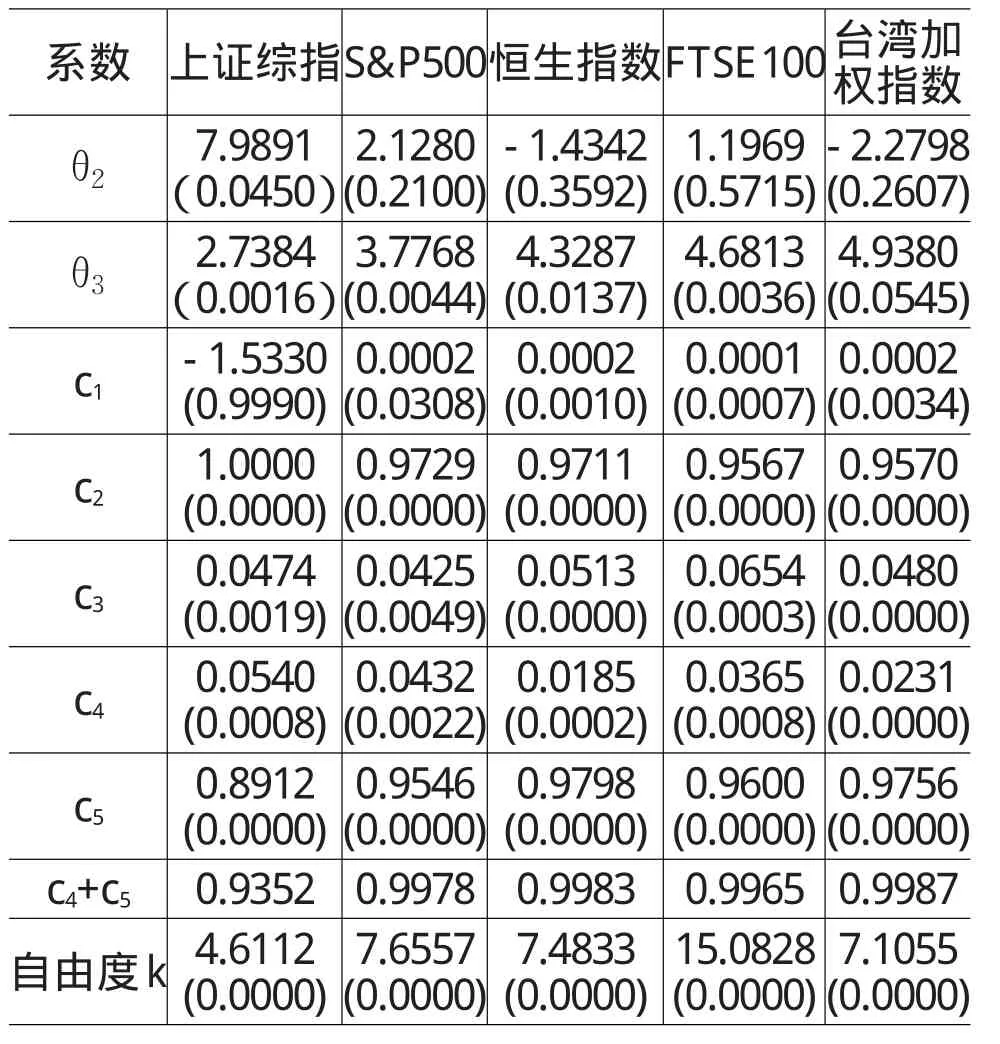
表2 模型结果

从结果来看，上证综指的长期和短期波动成分系数都具有统计显著性（在5%水平上），这表明短期波动成分和长期波动成分对上证综指回报都有解释能力。其他发达股票市场上，系数θ2都不显著，系数θ3都具有统计显著性（1%或5%水平上），表明长期波动成分对这些股票市场指数回报更有解释力，而短期波动成分则解释力不强。

系数c1表示长期波动成分的收敛趋势，FTSE为0.0001，其他指数为0.0002（因四舍五入关系，这些数值实际上并不相同）。系数c2表示长期波动成分的收敛速度，在计算结果中，其数值接近于1，表明长期成分将缓慢收敛。上证综指的c2等于1，表示其长期波动成分并不收敛于某一固定值，因此相应的系数c1不具有显著性。系数c4+c5表示短期波动的收敛速度，除上证综指之外其他四个指数，该值接近1且大于c2，说明短期成分收敛的速度比长期成分更慢；上证综指该值为0.9224，说明上证综指短期波动成分收敛速度相对较快。

（三）长、短期波动成分对比

由于上证综指的长、短期波动成分都有显著性，下面将计算分解出来的上证综指每日长、短期波动在图1中画出。

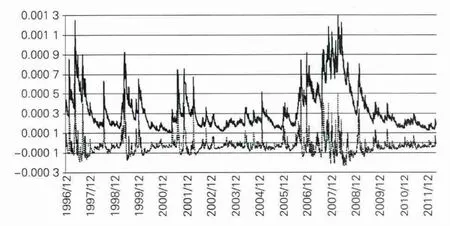
图1 上证综指长、短期波动成分对比

长期波动成分均大于0，短期波动成分在0附近变动。长期波动成分在一定期间内呈现出某种趋势，而短期波动成分则在0附近持续变动，二者有明显区别。

（四）长、短期波动成分对股指收益的贡献

根据公式（3），长期波动对Rt的贡献为 θ3qt，短期波动的贡献为θ2(ht-qt)。由于长、短期波动成分对上证综指回报都有显著影响，故重点分析长、短期波动对上证综指收益贡献的情况，见图2；为方便对比，图2也给出了长、短期波动对S&P500指数收益率贡献的情况（列出S&P500指数加以对比的原因是，在表2计算结果中，该指数的系数θ2的p值是除上证综指外最小的，因此更有可比性）。

从图2来看，上证综指短期波动成分的贡献有更大的波动性，而长期波动成分的贡献波动较平稳；短期波动成分对收益的贡献可能为负，而长期波动成分对收益的贡献均为正。S&P500指数情况与此类似，但短期波动成分的变动在大部分情况下不如上证综指的剧烈。在上证综指所有3879个交易日中，有1089个交易日的短期波动成分贡献度大于0，其余交易日贡献小于0。由此可见，上证综指短期波动对股指收益有较大影响，而且其影响方向不确定；长期波动给股指收益带来正向影响，但相对S&P500指数来讲影响程度较小。

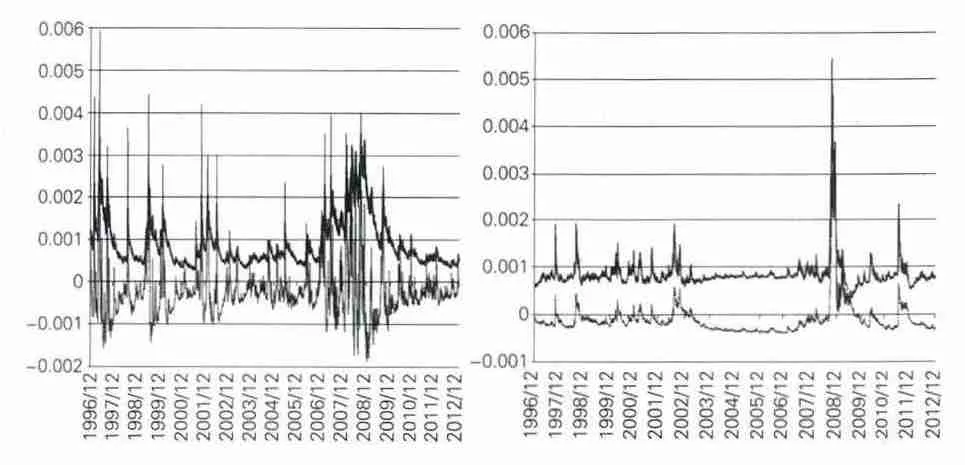
图2 长、短期波动成分对收益的贡献

为更准确地衡量长、短期波动成分对收益贡献的相对大小，计算长期波动贡献率λL和短期波动贡献率λS如下：

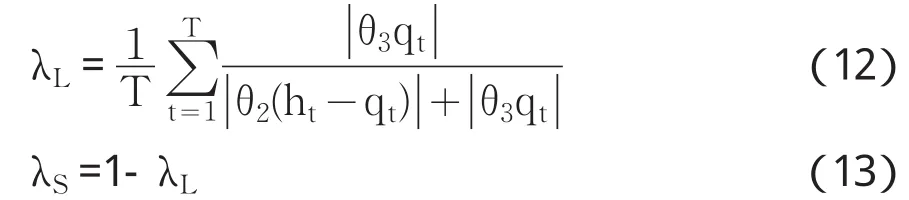
表3对比了各指数长、短期波动对指数收益的贡献率。相比较而言，上证综指的长、短期波动对指数收益的贡献率更接近；其他指数的长期波动贡献率均超过70%，明显超过短期波动。这也说明对中国股市来讲，长、短期波动成分具有类似的重要性，而其他股市上，长期波动具有更重要的意义。

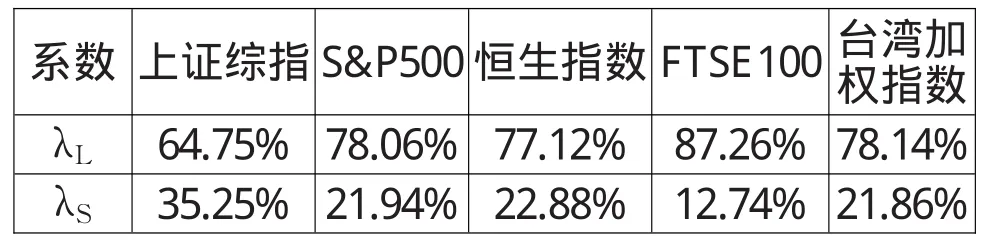
表3 长、短期波动成分对指数收益的贡献率

（五）模型拟合优度

若R2为负，则定价模型表现不如基准模型。对比结果见表4。

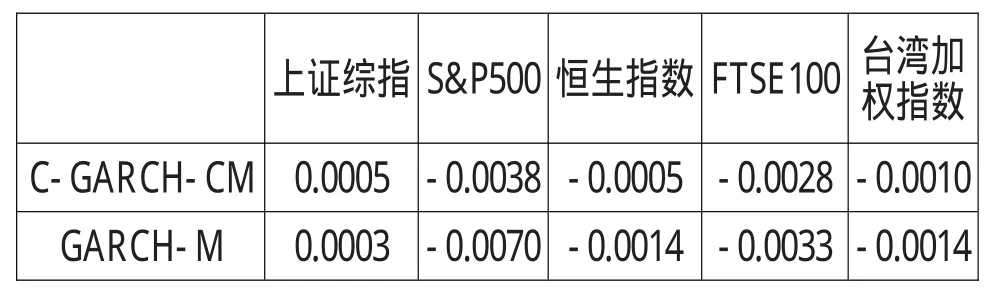
表4 各指数拟合优度对比

从表4来看，各股票指数的C-GARCH-CM模型的拟合优度比没有考虑波动期限成分的一般GARCH-M模型都略有提高，但除上证综指外，其他指数结果的可决系数都小于零。这表明，对于上证综指来讲，期限波动分解模型不仅好于没有考虑波动期限成分的一般GARCH-M模型，同时也好于随机游走模型。从前面的分析来看，只有上证综指的长、短期波动成分都有显著性，这可能是导致针对中国股票市场而言C-GARCH-CM模型优于GARCHM模型和随机游走模型的原因。

五、结论

通过上面的分析可以得出如下结论：

（1）在发达股票市场上，股票指数回报主要与长期波动相关，短期波动对股票回报解释力度不强。但中国股市回报不仅与长期波动相关，也与短期波动相关。这反映出中国股票市场风险—回报关系不同于发达市场。

（2）长期波动成分对各指数收益的贡献为正，而短期波动成分对指数收益的贡献多为负，这表明短期不确定性冲击对股市回报产生显著的负面影响。

（3）中国股票市场受短期波动影响较大。发达市场上，短期波动对指数收益的贡献率不到23%，而中国上证综指短期波动对指数收益的贡献率达到35%。

（4）相比一般的波动定价模型，波动成分分解的C-GARCH-CM模型的定价效果有一定的改善。

与发达国家不同，短期波动对中国股价指数回报有重要影响，这与中国股票市场投机氛围浓厚可能存在关系，如李心丹等发现，境内投资者的确存在过度交易的现象，年平均交易次数大大超过美国的水平[10]，过于频繁的交易无疑会加剧短期波动。中国股市投资者存在明显的偏重短线操作、忽视长期投资的特点，股票市场制度建设不成熟，市场机制有待完善，股票长期投资价值无法显现，从数据上就反映出我国股票指数回报受短期波动的影响明显。短期波动的明显影响显然不利于中国股票市场的长期健康稳定发展，这是证券监管部门在进行股票市场制度建设和风险管理时应当慎重考虑的问题。

[1]Scruggs JT.Resolving the Puzzling Intertemporal Relation between the Market Risk Premium and Conditional Market Variance:A Two-factor Approach[J].The Journal of Finance,1998,53(2):575-603.

[2]Adrian T,Rosenberg J.Stock Returns and Volatility:Pricing the Short-Run and Long-Run Components of Market Risk[J].The Journal of Finance,2008,63(6):2997-3030.

[3]Guo H,Neely C J.Investigating the Intertemporal Risk-return Relation in International Stock Markets with the Component GARCH Model[J].Economics letters,2008,99(2):371-374.

[4]Zarour B A,Siriopoulos C P.Transitory and Permanent Volatility Components:The Case of theMiddle East Stock Markets[J].Review of Middle East Economics and Finance,2008,4(2):80-92.

[5]Christ offers en P,Jacobs K,Ornthanalai C,et al.Option Valuation with Long-run and Short-run Volatility Components[J].Journal of Financial Economics,2008,90(3):272-297.

[6]宋逢明，李翰阳.中国股票波动性的分解实证研究[J].财经论丛，2004，（4）：23-28.

[7]张普，吴冲锋.股票价格波动:风险还是价值?[J].管理世界，2010，（11）：52-60，187.

[8]Bollerslev T.A Conditionally Heteroskedastic Time Series Model for Speculative Prices and Rates of Return[J].The Review of Economics and Statistics,1987,69(3):542-547.

[9]Chen M H.Risk and Return:CAPM and CCAPM[J].The Quarterly Review of Economics and Finance,2003,43(2):369-393.

[10]李心丹，王冀宁，傅浩.中国个体证券投资者交易行为的实证研究[J].经济研究，2002，（11）：54-63.

1003-4625（2014）06-0098-05

F832.5

A

2014-04-08

国家自然科学基金（71171056）。

黄祥钟（1978-），男，福建连江人，副教授，博士研究生，研究方向：金融市场与风险管理。

张艳峰）