云环境下基于二进制编码的Apriori改进算法

(郑州华信学院，河南 新郑 451100)

Apriori算法[1]改进一直是数据挖掘的一个重要研究方向，近年来，许多学者相继提出了基于向量积[2]、布尔向量[3]、最大频繁项集[4]等方法的改进算法。但是，面对海量数据时，这些算法就需要大量时间来扫描数据库，不利于频繁项集的快速寻找。本文将在云计算环境中，将Apriori算法与MapReduce模型结合，对海量数据进行分布式并行处理，最终产生符合要求的频繁项集，从而提高了数据挖掘效率[5-9]。

1 相关知识

1.1 Apriori算法

Apriori算法通过多次扫描事务数据库来计算各项集的支持度，利用候选项集来寻找n项频繁项集。该算法具有以下性质：

性质1 若L为频繁项集，则L的任何非空子集均为频繁项集[4]。

性质2 若L为非频繁项集，则L的任何超集均为非频繁项集[4]。

1.2 幂集与二进制编码

定义1 对任意集合A={I1,I2,…,In}，将A中所有子集的全体称为A的幂集，将A的幂集中所有元素个数为k的子集的全体称为A的k-幂集。

例如，对于集合A={I1,I2,I3}，则A的幂集为{Φ,{I1},{I2},{I3},{I1,I2},{I1,I3},{I2,I3},{I1,I2,I3}}，A的幂集中元素个数为2的子集为{I1,I2}，{I1,I3}，{I2,I3}，则其2-幂集可表示为{{I1,I2},{I1,I3},{I2,I3}}。

为了算法需要，后面约定幂集中不含空集。结合已有的二进制编码方法[10]，下面给出本文的二进制编码定义。

定义2 对任意集合A={I1,I2,…,In}，P⊆A，规定P的二进制编码为n位，且若Ii∈P，则编码的第i位用1表示，否则用0表示。

例如，对于集合A={I1,I2,I3}，若P={I1,I3}，则其二进制编码为101。

1.3 MapReduce模型

MapReduce模型是Google公司提出的、用于并行处理海量数据集的编程模型。该编程模型将待处理的事务数据库分割成若干子数据库，并分配给不同的节点进行处理。在每个节点中，该模型对接受到的数据进行解析，并以键值对的形式表示数据，利用Map函数对这些键值对进行处理，产生待合并的中间结果，再利用Reduce函数合并相同性质的中间结果，最终形成符合要求的结果。

2 云环境下基于二进制编码的Apriori改进算法

为了更好地处理海量数据，本文首先改造Map和Reduce函数，并对事务数据库进行处理，产生符合要求的结果，然后在云环境下将二进制编码思想应用于Apriori算法改进中，最终实现快速高效地寻找频繁项集的目的。

2.1 Map函数和Reduce函数的改造

2.1.1 Map函数的改造

输入：某个事务标识符First_key，该事务中项集的二进制编码First_value。

输出：，，…， // First_value1～ First_valuen为该事务中项集的k-幂集的二进制编码。

fori=1 ton

{

getisubset;//获取该事务中项集的k-幂集的第i个子集

get a binary encoding of this subset as First_valuei;//该子集用二进制编码First_valuei表示

output();//第i个子集的输出形式为

2.1.2 Reduce函数的改造

输入：某事务的k-幂集的//First_valuei中“1”的个数为k。

输出：//di用来记录该事务中所有值为First_valuei的中间结果个数。

intdi=1

forj=1 tom//m为所有中间结果个数

{if(First_valueiΛFirst_valuej==k)di=di+1;//通过“与”运算，寻找计算结果为k的中间结果，并用变量di记录}

output()//合并后的输出形式为

2.2 云环境下基于二进制编码的Apriori改进算法

为了更加高效地寻找频繁项集，本文将运用MapReduce模型对Apriori算法加以改进，具体算法可描述为：

Step1 将事务数据库D分解为大小相等或接近相等的子数据库，并分配给不同的节点；

Step2 对于每个节点，使用Map函数将事务的项集映射成k-幂集的对，产生该节点的候选k-项集；

Step3 对于所有节点，使用Reduce函数将候选k-项集合并，形成候选频繁k-项集，并将其支持度与最小支持度min_support进行比较，确定频繁k-项集。

通过上述算法改进，在寻找频繁项集时，通过分解事务数据库，利用Map函数和Reduce函数实现了数据的并行分布处理，大大提高了算法的效率。

3 实例分析

以事务数据库D=(TID, Itemset)为例 (如表1所示)，利用云环境下基于二进制编码的Apriori改进算法来寻找频繁2-项集[1]。在表1中，TID是事务标识符，Itemset是事务中的项集，设最小支持度min_support为2。由文献[1]可知，频繁1-项集为{I1，I2，I3，I4，I5}。

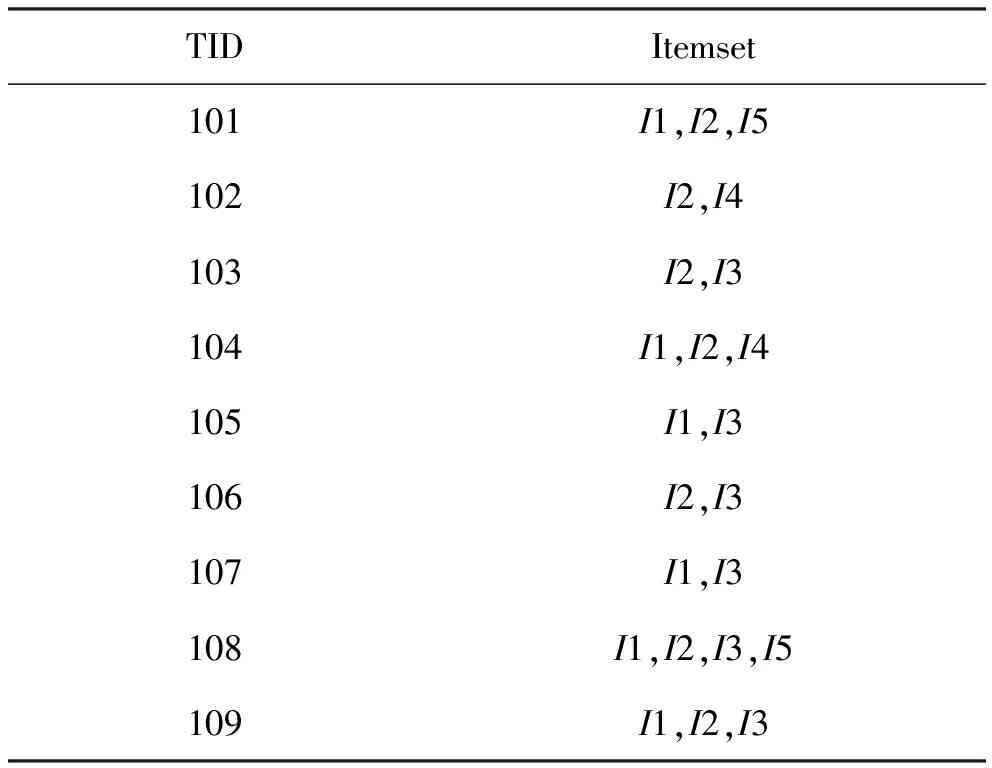
表1 事务数据库D

(1)将事务数据库D分解为3个子数据库D1、D2、D3，其中D1为{{101，{I1，I2，I5}}，{102，{I2，I4}}，{103，{I2，I3}}}，D2为{{104，{I1，I2，I4}}，{105，{I1，I3}}，{106，{I2，I3}}}，D3为{{107，{I1，I3}}，{108，{I1，I2，I3，I5}}，{109，{I1，I2，I3}}}，并将子数据库D1、D2、D3分别发送到节点R1、R2、R3(这3个节点主要用来并发处理3个子数据库的数据)。

在每个节点中，将子数据库的数据解析成形如的键值对，其中：

节点R1的键值对为：<101，{I1，I2，I5}>、<102，{I2，I4}>、<103，{I2，I3}>;

节点R2的键值对为：<104，{I1，I2，I4}>、<105，{I1，I3}>、<106，{I2，I3}>;

节点R3的键值对为<107，{I1，I3}>、<108、{I1，I2，I3，I5}>、<109，{I1，I2，I3}>。

(2)对不同的节点，使用Map函数将事务的项集映射成2-幂集的二进制编码形式。

在节点R1中，利用经过改造的Map函数对3个事务101～103中的项集进行处理，产生形如的中间结果：

Map(<101，{I1，I2，I5}>)={<11000，1>，<10001，1>，<01001，1>}；

Map(<102，{I2，I4}>)={<01010，1>}；

Map(<103，{I2，I3}>)={<01100，1>}。

在节点R2中，利用经过改造的Map函数对3个事务104～106中的项集进行处理，产生形如的中间结果：

Map(<104，{I1，I2，I4}>)={<11000，1>，<10010，1>，<01010，1>}；

Map(<105，{I1，I3}>)={<10100，1>}；

Map(<106，{I2，I3}>)={<01100，1>}。

在节点R3中，利用经过改造的Map函数对3个事务107～109中的项集进行处理，产生形如的中间结果。

Map(<107，{I1，I3}>)={<10100，1>}；

Map(<108，{I1，I2，I3，I5}>)={<11000，1>，<10100，1>，<10001，1>，<01100，1>，<01001，1>，<00101，1>}；

Map(<109，{I1，I2，I3}>)={<11000，1>，<10100，1>，<01100，1>}。

(3)对于3个节点R1、R2、R3，使用Reduce函数将First_value值相同的中间结果进行合并，形成形如的候选频繁2-项集[10]：

Reduce(<11000，1>)=<11000，4>；

Reduce(<10001，1>)=<10001，2>；

Reduce(<01001，1>)=<01001，2>；

Reduce(<01010，1>)=<01010，2>；

Reduce(<01100，1>)=<01100，3>；

Reduce(<10010，1>)=<10010，1>；

Reduce(<10100，1>)=<10100，3>；

Reduce(<00101，1>)=<00101，1>。

再将候选频繁2-项集的支持度d和最小支持度min_support=2进行比较，得到频繁2-项集为：

{<11000，4>，<10001，2>，<01001，2>，<01010，2>，<01100，3>，<10100，3>}。

最后，将频繁2-项集的二进制形式转换为项集形式，可得：

{{I1，I2}，{I1，I5}，{I2，I5}，{I2，I4}，{I2，I3}，{I1，I3}}。

同样地，当k为其他值时，也可按此过程求频繁k-项集。

4 结 语

通过分析Apriori算法的不足，本文引入MapReduce模型，改造了Map和Reduce函数，结合幂集的二进制编码方法，提出了云环境下基于二进制编码的Apriori改进算法，一定程度上提高了海量数据的频繁项集挖掘效率，为关联规则挖掘提供了新的研究方向。

参考文献：

[1] Han Jiawei, Micheline Kanber.数据挖掘概念与技术[M].范明,孟小峰,译.北京:机械工业出版社,2001.

[2] 刘以安,羊斌.关联规则挖掘中对Aprior算法的一种改进研究[J].计算机应用,2007,27(2): 418-420.

[3] 李志林,戴娟,刘以安.基于布尔向量运算的Apriori算法[J].江南大学学报(自然科学版), 2010,9(3):270-273.

[4] 吉根林,杨明,宋余庆，等.最大频繁项目集的快速更新[J].计算机学报,2005,28(1): 128-135.

[5] 张圣.一种基于云计算的关联规则Apriori算法[J].通信技术,2011,44(6):141-143.

[6] 张恺,郑晶.一种基于云计算的新的关联规则Apriori算法[J].甘肃联合大学学报(自然科学版),2012,26(6):61-64.

[7] 吴琪.基于云计算的Apriori挖掘算法[J].计算机测量与控制,2012,20(6):1653-1655.

[8] 谢宗毅.关联规则挖掘Apriori算法的研究与改进[J].杭州电子科技大学学报,2006, 26(3):78-82.

[9] 曾舸,刘先锋.关联规则挖掘中Apriori改进算法的研究[J].计算机与现代化,2007(1):46-48.

[10] 叶晓波.一种基于二进制编码的频繁项集查找算法[J].楚雄师范学院学报,2009,24(3): 13-19.