一个生成组合的新算法
2011-03-15殷剑宏
殷剑宏, 罗 珣
(合肥工业大学计算机与信息学院,安徽合肥 230009)
在许多学科中,组合在理论与应用上都起着重要作用。n个元素集合{1,2,…,n}的组合个数为。在工程应用中,常常需要列举出这2n个组合,即寻找一个将集合{1,2,…,n}的2n个组合列出的系统过程,换句话说,就是要寻找一种生成集合{1,2,…,n}的所有组合的算法。由于n个元素集合{1,2,…,n}的组合个数很大,为了使算法在计算机上有效地运行,算法的每一步执行起来必须简单,算法的结果必须是一个表,该表包含集合{1,2,…,n}的每一个组合,且每一个组合只出现1次。
由于集合{1,2,…,n}的组合就是其子集,这样可以利用集合{1,2,…,n}的子集和n位二进制数之间的一一对应关系:如果i在子集中,对应的n位二进制数在位置i为1;如果i不在子集中,对应的n位二进制数在位置i为0。这样,如果可以列出所有的n位二进制数,那么通过n个元素集合{1,2,…,n}的组合与n位二进制数之间的一一对应关系,就可以列出n个元素集合{1,2,…,n}的所有组合。
由于n位二进制数有2n个,决定了生成所有n位二进制数算法的时空效率均为O(2n),即为指数复杂性。文献[1-9]引入的字典序法,只能由一个n位二进制数生成下一个n位二进制数。本文推导出一个生成所有n位二进制数的新算法,该算法具有以下优势:理论只是初等的,且算法描述非常通俗易懂;算法的结果是一个表,该表包含每个n位二进制数1次且仅1次;算法不必保留所有n位二进制数的列表,就能够简单地用后面的n位二进制数覆盖当前的n位二进制数;算法是循环的;算法的每一步执行起来非常简单,算法程序化特别容易,确保能在计算机上有效地运行,大大地方便了工程应用。
1 算法的归纳描述
n位二进制数可划分为以下2类:
(1)将0插入每一个n-1位二进制数后,得到2n-1个不同的n位二进制数。
(2)将1插入每一个n-1位二进制数后,得到2n-1个不同的n位二进制数。
由加法原理,得到2n-1+2n-1=2n个不同的n位二进制数。
从一位二进制数开始具体归纳描述如下:
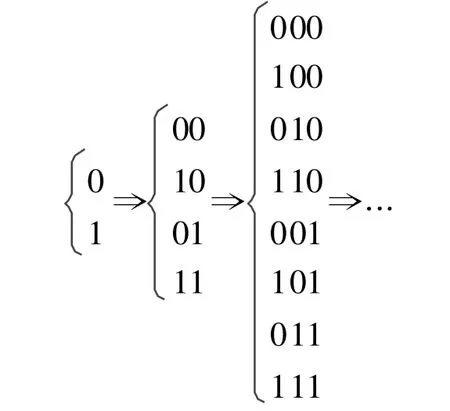
上述归纳描述已清楚地明确对任意正整数n,如何进行生成所有n位二进制数的系统过程。同时显示该方法恰好生成2n个不同的n位二进制数,且每一个n位二进制数只出现1次,其中:①第1个n位二进制数为00…0,最后一个n位二进制数为11…1;②第2n-1个n位二进制数为11…10,第2n-1+1个n位二进制数为00…01;③前2n-1个n位二进制数末位上的数字均为0,后2n-1个n位二进制数末位上的数字均为1。
定理1 按上述归纳描述,n位二进制数a0 a1…an-2 an-1所处位置数为a0×20+a1×21+…+ an-2×2n-2+an-1×2n-1。
证明 (1)定理对于n=1,2时,显然成立。
(2)假设定理对于n-1成立,即n-1位二进制数a0 a1…an-2按上述归纳描述,其所处位置数为a0×20+a1×21+…+an-2×2n-2。考察n位二进制数a0a1…an-2an-1,若an-1=0,则n位二进制数a0 a1…an-2 an-1与n-1位二进制数a0 a1…an-2的位置数相同,即n位二进制数a0 a1…an-2an-1的位置数=a0×20+a1×21+…+an-2× 2n-2=a0×20+a1×21+…+an-2×2n-2+0× 2n-1=a0×20+a1×21+…+an-2×2n-2+an-1× 2n-1;若an-1=1,则n位二进制数a0a1…an-2an-1的位置数=n-1位二进制数a0 a1…an-2的位置数+2n-1=a0×20+a1×21+…+an-2×2n-2+ an-1×2n-1。
由数学归纳法,定理得证。
但是,上述归纳描述指出,要生成所有n位二进制数,必须首先生成所有n-1位二进制数;而为了生成所有n-1位二进制数,又必须先生成所有n-2位二进制数等。然而,想做且仅能做的就是一次一个地生成n位二进制数,为了生成下一个n位二进制数而仅仅使用当前n位二进制数。且由于n位二进制数的数目很大,这就要求不必保留所有的n位二进制数列表就能够简单地用后面的n位二进制数覆盖当前的n位二进制数。同时,要求生成n位二进制数11…1时算法终止。
下面对上述归纳过程换种方式描述,即得到符合这些要求并按上述相同的顺序生成n位二进制数的算法。
当n=4时的情形:
从4位二进制数a0a1a2a3=0000开始
0000(当前二进制数中a0=0,改变a0)
1000(当前二进制数中a0=1,a1=0,改变a0,a1)
0100(当前二进制数中a0=0,改变a0)
1100(当前二进制数中a0=1,a1=1,a2=0,改变a0,a1,a2)
0010(当前二进制数中a0=0,改变a0)
1010(当前二进制数中a0=1,a1=0,改变a0,a1)
0110(当前二进制数中a0=0,改变a0)
1110(当前二进制数中a0=1,a1=1,a2=1,a3=0,改变a0,a1,a2,a3)
0001(当前二进制数中a0=0,改变a0)
1001(当前二进制数中a0=1,a1=0,改变a0,a1)
0101(当前二进制数中a0=0,改变a0)
1101(当前二进制数中a0=1,a1=1,a2=0,改变a0,a1,a2)
0011(当前二进制数中a0=0,改变a0)
1011(当前二进制数中a0=1,a1=0,改变a0,a1)
0111(当前二进制数中a0=0,改变a0)
1111(当前二进制数中a0=a1=a2=a3=1,算法终止)
具体算法描述如下:
从n位二进制数a0a1…an-2an-1=00…00开始,当a0 a1…an-2 an-1≠11…11时:①从左向右扫描找最小的整数j使得aj=0;②改变a0,a1,…,aj的值(即a0,a1,…,aj-1的值均由1变为0; aj的值由0变为1)。
注意:对于最后一个 n位二进制数a0 a1…an-2 an-1=11…11,由于a0=a1=…=an-1=1,从而改变a0,a1,…,an-1的值得到其直接后继n位二进制数00…00,因此算法是循环的。
定理2 上面描述的算法,对每个正整数n产生2n个不同的n位二进制数。
证明 (1)算法用于n=1,2时,定理显然成立。
(2)假设算法用于n-1时,产生2n-1个不同的n-1位二进制数。
设当前n位二进制数为a0 a1…aj-1 aj a j+1…an-2 an-1,其中a0=a1=…=aj-1=1,aj=0。
若j=n-1,即a0 a1…an-2 an-1=11…10,则a0a1…an-2an-1是第2n-1个n位二进制数,改变a0,a1,…,an-1的值,显然得到第2n-1+1个n位二进制数为00…01。
若j≠n-1,则a0a1…aj-1ajaj+1…an-2an-1一定不是第2n-1个n位二进制数,换句话说,a0 a1…aj-1 aj a j+1…an-2 an-1的直接后继n位二进制数末位上的数字仍为an-1。又a0a1…aj-1ajaj+1…an-2是n-1位二进制数,改变a0,a1,…,aj-1,aj的值即得其直接后继n-1位二进制数00…01 aj+1…an-2。因此,n位二进制数为a0 a1…aj-1 aj aj+1…an-2 an-1的直接后继n位二进制数为00…01 aj+1…an-2an-1。由数学归纳法,定理得证。
2 举 例
生成6位二进制数,结果用4列显示,其中第1列为前16个6位二进制数,第2列为顺数第2个16个6位二进制数,…,最后一列为最后16个6位二进制数。
000000 000010 000001 000011
100000 100010 100001 100011
010000 010010 010001 010011
110000 110010 110001 110011
001000 001010 001001 001011
101000 101010 101001 101011
011000 011010 011001 011011
111000 111010 111001 111011
000100 000110 000101 000111
100100 100110 100101 100111
010100 010110 010101 010111
110100 110110 110101 110111
001100 001110 001101 001111
101100 101110 101101 101111
011100 011110 011101 011111
111100 111110 111101 111111
3 结束语
本文首先以加法原理为理论,得到一个将所有2n个n位二进制数列出的系统过程,深刻分析了该系统过程的内在本质,进而得到一个易于计算机处理的归纳描述,且只用到数学归纳法的思想,并进行了理论上的证明。本文给出的算法,其理论只是初等的,算法描述非常通俗易懂,且是循环的;同时算法的结果是一个表,不必保留所有n位二进制数的列表,能够简单地用后面的n位二进制数覆盖当前的n位二进制数,且算法的每一步执行起来非常简单,因而易于计算机处理,大大方便了工程应用。
[1] 陈景润.组合数学简介[M].天津:天津科学技术出版社,1988:42-55.
[2] Reingold E M,Nievergelt J,Deo N.Combinatorial algorithm s:theory and practice[M].Englew ood Cliffs,NJ: Prentice H all,1977:111-120.
[3] Trotter H F.A lgorithm 115[J].Communications of the Association for Compu ting Machinery,1962,5:434-435.
[4] Even S.A lgorithm ic combinatorics[M].New York:Macm illan,1973:67-79.
[5] Brualdi R A.Introductory combinatorics[M].北京:机械工业出版社,2003:81-93.
[6] Brualdi R A.组合数学[M].冯舜玺,罗 平,裴伟东,译.北京:机械工业出版社,2003:50-57.
[7] Roberts F S,Tesm an B.应用组合数学[M].冯 速,译.北京:机械工业出版社,2007:60-61.
[8] 殷剑宏.组合数学[M].北京:机械工业出版社,2006: 12-18.
[9] 殷剑宏,汪荣贵,薛 峰.生成图的全部极大独立集的一般方法[J].合肥工业大学学报:自然科学版,2008,31(3): 479-483.
