初中数学“微变教学”策略研究
2014-03-27汪东如
汪东如
摘 要:微变教材,精心备课;微变教学,活化课堂;微变作业,活跃思维。以新浙江教育版的实例,结合初中数学新课程标准(2011年版)的部分精神,分析了微变教学的策略。
关键词:微变教学;策略;新课标
《義务教育数学课程标准(2011年版)》中指出“教师教学应该以学生的认知发展水平和已有的经验为基础。”这不单单符合人的智力水平发展规律,更为初中数学教学指明了方向。利用微变教学,关键还是抓住教学的三个环节:微变教材,精心备课;微变教学,活化课堂;微变作业,活跃思维。
一、微变教材,精心备课
活用教材是提高数学课堂教学成效的有效措施。例如教师在对一元二次方程的知识备课时,要充分认识到方程知识的连续性和递进性:七年级学习了一元一次方程的定义、解法、应用,而一元二次方程的定义、解法、应用则在八年级下册中学习。在备课时教师首先要预设学生回顾一元一次方程的定义:等号两边都是整式,只含有一个未知数,并且未知数的最高次数为一次的方程叫做一元一次方程。着重点出一元一次方程的三个要素:整式、一个未知数、最高次为1次,然后根据一元二次方程和一元一次方程名称中的“微变”,即“一次”变为“二次”,可以直接让学生回答一元二次方程的定义,这个时候不管是学困生还是优等生都能非常轻松地回答,因为在定义上只有一个地方发生了变化,学生只要将最高次改为2次就能很完整地说出定义了,这种只存在细微的变化会给学生一种熟悉感,让他们有法可思,有迹可循。
二、微变教学,活化课堂
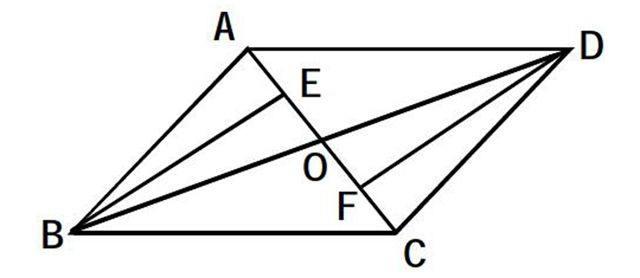
微变教学模式为解决矛盾提供了捷径,教师可以用较小的精力来活化课堂,既达到了改革的目的,也活跃了课堂教学模式。例如:新浙江教育版八年级下册中第四章平行四边形的性质,教材安排了练习题:“已知:如图,?荀ABCD的对角线AC,BD交与点O,E,F分别是OA,OC的中点.求证:△OBE≌△ODF.”
此题是平行四边形的对角线互相平分的性质的应用。教师在教学过程中要能够应用“微变教学”模式则能达到事半功倍的效果,首先,教师可以微变条件,将条件中的“E,F分别是OA,OC的中点”改为条件“AE=CF”或者“OE=OF”,还可以改为“点E和点F分别在CA和AC的延长线上,且AE=CF”,这些条件的微变均是通过“SAS”来证明△OBE≌△ODF。根据全等三角形的判别方法,教师可以让学生来微变条件,根据“ASA”、“AAS”,可以将条件改为“∠EBO=∠FDO”或“∠BEO=∠DFO”,甚至还可以将条件改为“∠ABE=∠CDF”、“BE⊥AC、DF⊥AC”等等。
教师还可以微变结论,把所求证的结论“△OBE≌△ODF”改为“∠EBO=∠FDO”或者“BE=DF”等等。
教师还可以微变教材的顺序,将后面的平行四边形的判别方法的知识也融入本题中,即将DE、BF连结,求证四边形BFDE是平行四边形。学生可以结合上面的微变条件,通过不同的平行四边形判别方法来证明四边形BFDE是平行四边形。
同样的一个题目,教师通过微变条件、微变结论、甚至微变教材的内容顺序等手段,将一个题目演变成了几个题目,甚至十几个题目,使教师课堂的教学容量有很大的提高,对培养学生的分析思维能力和归纳总结能力有很大的帮助。
三、微变作业,活跃思维
1.微变数学课堂作业
例如:教师在讲解二次根式的性质()2=a(a≥0)与=a=a(a≥0)-a(a<0)时,对于教材中的课堂作业题,教师可以先让学生自己找一找,这些题目分别对应两个性质中的哪一个,而不是一上来就让学生做,这样有预设的让学生思考实际上是一种归纳与总结,学生通过观察发现课堂作业题与例题的差别,抽象出本质。
2.微变课后作业
与教材配套的作业本作业具有大众性,适合于大多数的学生,但是并不是所有的学生,作业虽然具有了层次性,但是没有考虑学生的差异性,缺乏针对性,使得成绩优秀的学生一方面做无谓的重复,另一方面又吃不饱,而学困生又由于认知水平的差异,对许多题目束手无策,学习越来越没有兴趣,导致有许多学生每次作业均有几个题目是空白的,久而久之,则变为放弃,而且这些学生会认为这些题目肯定不会,形成了一种不愿意去思考的不良学习数学的习惯。教师对这些学习态度上出现问题的学生更是没有办法,集体讲解效果不佳,个别辅导没有时间,毕竟学生人数太多了。
而如果教师对作业本作业也进行微变,将所给的作业本作业题根据其难度分层情况与学生学习程度情况进行整合,形成一对一的对应关系,有选择性地让学生做。
微变教学模式,通过微变教材、微变课堂、微变作业,丰富了原有的上课形式,让教师从原来的教学模式中解放出来,使学生缺少思考的时间,甚至出现上课来不及的现象,把一节内容分成两个课时,既加重了教师的负担,也加重了学生的负担。当然,微变教学模式通过微变最终的目的是让学生能够发现变中的不变,掌握知识点的本质,以不变应万变。
编辑 董慧慧