基于AHP和模糊综合评判的大学生体质健康状况评价

陈航

（衡阳师范学院 体育系，湖南 衡阳 421002）

基于AHP和模糊综合评判的大学生体质健康状况评价

陈航

（衡阳师范学院 体育系，湖南 衡阳 421002）

加强大学生体质健康综合评价的研究，对于科学地评价与监测大学生的体质健康状况具有重要的现实意义.采用特尔菲法选取13项指标建立了大学生体质健康评价体系，运用AHP方法确定了各指标的权重；结合模糊综合评判法，建立了大学生体质健康状况量化评价的数学模型.结果显示该评价模型合理、实用、可信度高.

大学生；体质健康；评价模型；综合评价

中国从1979年开始的大规模全国体质调查，为社会、经济、教育等事业的发展提供了宝贵的基础数据资料.在高校中开展体质测试始于上世纪80年代后期实行的《大学生体育锻炼标准》，这也是高校体质监测工作开展的初期，由此展开的工作多数是群体性质，几把皮尺和几块秒表就解决了测试问题，没有得到广大体育教师和学生的足够重视，也没有相应的评价体系.随着社会的高速进步，人们对自身体质的评价也越来越重视，这不仅仅是个人的健康问题，不仅仅是学校发展的问题，而是全民族是否能兴旺发达，是否能繁荣昌盛的问题.随着高校体育新发展的需要，体质监测逐渐开始发挥重要作用，从国家到地方无不开始对体质监测工作进行大力度的加强，这是从培养人才、锻炼人才、保护人才的角度考虑的社会问题，是高校体育科研工作发展进程中一次“承前启后，继往开来”的重要改革.

鉴于此，本研究拟以大学生体质健康状况为研究对象，运用特尔斐法对影响大学生体质健康状况的指标进行构建与选取，然后运用层次分析法确定了个指标的权重值，最后通过模糊数学的理论建立了大学生体质健康评价的数学评判模型，为量化评价大学生体质健康的状况提供理论依据.

1 评价指标体系的确定

评价指标体系的建立是整个评价工作能否正确进行的基础，测量与评价的可靠性，在很大程度上取决于所选择或设计指标的有效程度.建立一个合理，可行的分析评价模型，必须首先建立一个有效的评价指标体系.

收集、整理有关的文献资料，设计出影响大学生体质健康的结构问卷，通过函调的形式向相关研究领域的3名专业教师征询意见，确定问卷的内容效度和结构效度；然后经过3轮特尔斐法调查，选取出4大类13项指标（见表1）.

表1 大学生体质健康状况评价指标体系

2 用AHP层次分析法确定各评价因素的权重

与传统加权评分模型使用主观去判断决定权重方法不同，AHP使用一种简单的方法将这种主观判断加以量化.这个方法的基础就是目标相对重要性的比较值，其基本步骤是:建立递阶层次结构；采用1-9的比率标度方法两两比较构造判断矩阵（见表2）；求解判断矩阵的最大特征根及其对应的正规化特征向量，该特征向量的各分量即为同一层各因素相对于上一层某因素相对重要性的排序权值.

2.1 建立一级指标的判断矩阵，确定其权重

根据AHP层次分析法的计算方法,建立AHP层次分析的判断矩阵,如表2

表2 AHP层次分析的判断矩阵

根据AHP层次分析的判断矩阵，计算一级指标判断矩阵的权向量W(见表3)

其中：n为判断矩阵的阶数（n=4）；aij为判断矩阵的因素；Wi为权向量的第i个因素；则得权向量：W=（0.104，0.271，0.571，0.055）T

2.2 建立二级指标的判断矩阵，确定其权重并检验

2.2.1 计算二级指标的权重

同样根据AHP层次分析法和上述积分法，在分别建立二级判断矩阵的基础上，分别求出各二级指标合成的相应权值，得各项指标对目标的重要程度，即各因素在系统中的重要程度.如表4所示.

2.2.2 进行一致性检验

应用公式CR=CI/RI对上述判断矩阵进行检验，代入数据，CR=(CI/RI)=0.085<0.10，故认为上述判断结果具有满意的一致性.

表3 权向量W的计算表

3 建立大学生体质健康状况综合评价的数学模型

大学生体质健康状况是一种由多方面因素构成的综合体.这一综合体，既可以在学生的日常生活中表现出来，又具有一定的模糊性，需要运用模糊集合论研究.

设U是所研究能力的因素集,U={u1u2… un}；V是评价语素,U={v1v2…vn}；再设第i因素的单因素评价为Ri,Ri={ri1ri2…rin},其中i=1,2,…m,且0≤rij≤1,表示从第i个因素着眼,对被评对象做出的第j种评语就是评语集V上的一个模糊子集.则R可用隶属度rij所构成的评价矩阵表示为:

表4 合成权重层次总排序一览表

又U上的模糊子集A(u)称为权重，A={a1a2… an},其中ai≥0，且有

依据模糊数学理论，对评判对象的综合评价结果B的数学模型为:

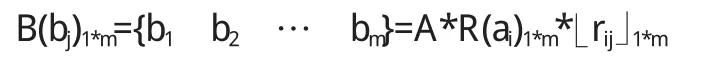
3.1 单因素模糊评价

单因素评价,就是相对于评价因素Uk分别作出评价Vk，即建立一个从Uk到Vk的关系fk:uki→(ri1(k)ri2(k)… rink(k))，由f可得单因素模糊评价距阵：

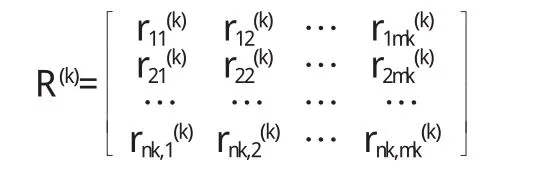
3.2 因素类综合评价

即若A(k)=(a1(k)a2(k)… ank(k))是因素Uk的权重,则因素类综合评价为:B(k)=A(k)*R(k)

3.3 大学生体质健康状况综合评价

即若C=(c1c2… ck)是因素类U的权重，则大学生体质健康状况评价成绩为：D=C*B(k)

3.4 将评价结果矩阵转换为评价分值

即若建立等级分数矩阵，则综合评价分值为：X=D*Z

4 评价模型可靠性，有效性及可行性检验与分析

为检验本研究所构建的分析评价模型在实际运用中的信度、效度与可行性，本研究运用该模型对部分高校大学生体质健康状况进行了抽样分析评价，并将评价结果同《国家学生体质健康标准》测试给出的评定结果分别做了信度和效度的关联分析：其信度为0.878,效度为0.923，P值均小于0.01.这说明本研究所构建的分析评价模型合理、可靠、有效.

〔1〕祁国鹰,等.实用体育统计学[M].北京:北京体育大学出版社,1995.

〔2〕尹少丰.可拓评价方法在优秀男子羽毛球运动员竞技能力状态诊断中的应用[J].北京体育大学学报,2013,36(3): 133-136.

〔3〕彭建军.体育院系学位论文工作质量综合测评指标体系与方法的研究[J].武汉体育学院学报,2000,34(6):114-117.

〔4〕陈航,尹少丰.师范院校体育教育专业网球普修课程考评体系的构建[J].宜春学院学报,2009,31(6):206-208.

G804.49

A

1673-260X（2014）02-0087-02