胶版印刷机橡皮布蠕变行为及其对印刷的影响

刘澎 , 赵宁, 张海燕

(1.西北工业大学 机电学院，陕西 西安 710072；2.西安理工大学 印刷包装工程学院，陕西 西安 710048)

胶版印刷是目前印刷领域占据主导地位的印刷方式。进行胶版印刷的印刷机称为胶版印刷机，简称胶印机。胶印机具有印刷速度高、印刷品质好、色调丰富等特点。在全球的印刷市场中，胶印占据了65%～70%市场份额[1]。胶印机的显著特征就是采用了橡皮滚筒，这也是胶印机名称的缘由。图1所示为胶印机的原理示意图。在胶印中，印版上的图文部分和空白部分几乎处于同一平面，图文部分亲油憎水，空白部分亲水憎油，利用“油水互斥”的原理形成版面。薄板状的印版包裹、安装在印版滚筒上，橡皮滚筒上包裹、安装有印刷用橡皮布。印刷时，输水系统先给印版传递润版液，使空白部分形成拒墨水膜，然后输墨系统给印版传递油墨，图文部分粘附油墨，从而构成印刷版面。印版滚筒通过对滚接触将承载印版图文的油墨传递给橡皮滚筒，当纸张从橡皮滚筒与压印滚筒之间通过时，在印刷压力作用下，油墨经橡皮滚筒转移到纸张的表面，完成印刷过程[2]。

图1 胶印机原理示意图

尽管胶印机属于自动化程度比较高的设备，但是对操作人员的经验依然十分依赖。当设备在印刷时，操作者需要抽取印品，观察印刷质量，调节油墨供给量。尤其是在改变印刷速度的时候，印刷机不能精确地随动改变输墨量，需要人工反复观察调节。这样的操作模式，不仅产生大量的废品,造成成本增加，而且影响印刷效率。究其原因，造成这种局面是因为目前胶印机油墨传递机理还处于定性的描述阶段，还没有得到精确的传递机理，不能对承印物上的油墨量进行精确预测。目前应用比较多的研究方法是应用图论理论仿真研究具体机型、具体墨路的墨流分布、传递量，墨路优化等问题，不涉及精确的理论接触模型，也就无法考虑接触压力、材料特性、墨流分裂位置等关键因素，自然也就谈不上精确的传递机理[3]。

研究胶印机油墨的精确传递机理对于提高胶印机的自动化与智能化水平、降低调机试印成本、控制质量波动、提高生产效率意义重大。2013年9月我国工业和信息化部在发布的《产业关键共性技术发展指南》中，将“高端、智能化印刷机墨色控制系统技术”列为发展高档印刷装备第一项亟需研究解决、优先支持的关键共性技术[4]。尽管国际著名印刷设备制造企业在胶印机油墨控制研究的初级技术——“油墨预置技术”方面走在前列，但由于胶印机油墨传递的复杂性,通过建立精确的油墨传递模型以获得更准确的输出墨量方面,目前还普遍存在许多难点，因此一般采用实验拟合的方法获得特定机型印品墨量与墨键开度等参数之间的关系式[5]。就“油墨预置技术”而言，仍然存在精度差、需要人工干预的缺憾，更别提智能化的胶印机墨量在线测控技术了。从这方面来讲，技术人员还需要开展更深入的研究工作[6]。

胶印机油墨的精确传递机理的研究止步不前，主要原因是这种有胶印橡皮布、油墨参与其中的接触问题属于复杂的接触力学问题[7]。就橡皮布而言，橡皮布属于粘弹性材料，既有弹性，又有粘性，在滚压接触过程中，会产生蠕性形变，接触区域的压力分布也不均匀，而且随时间而改变。采用简化的研究方法可将橡皮布视作非时变的弹性体来看待，但这不符合橡皮布的物理特性，因此简化该研究得到的结论与实验研究的结果往往有相悖之处(具体内容见本文数值计算部分)。

纳米压痕技术是通过计算机控制载荷连续变化，在线监测压深量，由于施加的是超低载荷，加之监测传感器具有优于1 nm 的位移分辨率，所以可以获得小到纳米级的压深，它特别适用于测量薄层、镀层、微机电系统中的材料等微小体积材料力学性能，可以在纳米尺度上测量材料的各种力学性质，如载荷-位移曲线、弹性模量、硬度、应变、粘弹性或蠕变行为等[8]。纳米压痕技术的载体是纳米压痕仪。纳米压痕仪用于研究片状结构材料、小块材料、功能梯度材料等的力学特性与粘弹性行为的应用研究越来越多[9]。胶印橡皮布是厚度为1.6～2.0 mm且表面平整的片状结构，本文正是通过理论分析与纳米压痕仪实验测定相结合的方法来研究橡皮布的粘弹性行为，然后应用弹流润滑理论建立接触模型，经数值计算研究橡皮布粘弹性行为对印刷油墨传递产生的影响。

1 理论分析

使用纳米压痕仪实验时，压头末端有球形、棱锥形、圆柱平面等不同形状与不同尺度的压头可以选用。在本研究中，考虑到胶印橡皮布的力学特性与组织构造特点，采用末端为球形的压头，因此下面的理论公式都是基于球形压头进行推导的。

关于刚性的压头压入线弹性材料的接触问题，Sneddon[10]给出了压头压力与位移之间的关系式(1)：

(1)

式中P代表压头负载的压力，R代表球形压头球形部分的半径，υ代表泊松比，G是剪切模量，D代表压头末端压入线弹性材料的位移。

刚性的压头压入由线粘弹性材料构成的半空间时，这种接触属于具有移动接触区域的准静态边界值问题[11]。换而言之，压头与半空间的接触边界是随时间而改变的。对于这种问题，Lee和 Radok提出了应用遗传积分算子来解决的方法。将遗传积分算子带入公式(1)中，可以得到给定压头任意加载历程时，具有时间依赖性的压头位移公式(2)：

(2)

式中J(t)代表在t时刻的蠕变柔量。

如果压头加载历程的函数是P(t)=a0t，即斜坡加载，式中a0代表加载函数的斜率。将加载的历程函数P(t)代入公式(2)，得到如下等式：

(3)

粘弹性材料的模型使用广义的Voigt模型[12]，那么蠕变函数的形式为：

(4)

式中J0，J1，…,JN是柔量分量，τ1，τ2，…,τN是滞后时间，N是正整数。

将公式(4)代入公式(3)，可得:

(5)

由于P(t)=a0t，因此公式(5)可以改写为如下形式：

(6)

2 实验测试

2.1 实验主要设备

实验所用纳米压痕仪为英国MicroMaterials公司的Nano Test system，如图2所示。与传统的测试设备相比，纳米压痕仪突出的优势在于其精度，以及排除了测试中人为因素的影响。测试前按要求输入相关参数，随后的测试则由设备自动完成。该纳米压痕仪依据研究者预设加载函数加载，按照设置的采样间隔时间自动记录时间、压头压力、压头位移等实验数据。

图2 纳米压痕仪

2.2 测试过程

1)压痕仪压头尺度的选择

实验首先需要对印刷橡皮布的表面形貌进行研究，选择合适尺度的压头。压头的尺度不能过小。过小尺度的压头，一则会产生“针刺效应”，压头会刺入橡皮布内部；二则所测数据偏差太大，处理难度大，实验意义不大。实验计划测试两种印刷橡皮布，研究中分别被称作橡皮布A与橡皮布B。实验中使用白光干涉仪分别对两种橡皮布表面进行观测，图3为这两种橡皮布的表面形貌影像，每幅影像包括橡皮布表面二维形貌、三维形貌和剖面形貌。经综合考虑，笔者选取的是末端半径为400 μm的球形标准压头。从图3可知，所选压头的尺度不会产生“针刺效应”，数据也具有相对稳定性。

图3 橡皮布的表面形貌影像

2)橡皮布的处理与装卡

压痕实验前，将印刷橡皮布切成40 mm×40 mm的方块状待检测样品，胶粘固定于测样夹具的底座上，静置6 h以上，使其与环境状况一致。用高压气流冲刷清洁橡皮布表面，然后等待实验实测。

3)实验参数设置

压头的加载采用斜坡加载，将加载函数P(t)=0.01tmN输入测试系统，数据采样间隔设置为0.02 s，每0.02 s记录一组压头压力及位移数据。对检测样品上测试点位进行规划，将规划点位输入测试系统。实验测试了两种印刷橡皮布，每种橡皮布检测样品测试了49个不同的点位。启动纳米压痕仪之后，人工的工作就结束了，测试系统会按预设加载曲线加载，每0.02 s记录一组实验数据。当在一个点位位置完成加载历程，会自动定位下一个加载点位，开始加载与记录数据，直至遍历所有规划点位，完成整个实验。实验环境温度为23℃，湿度为50%。

2.3 数据处理及其结果

将得到的实验数据进行处理，得到橡皮布的压力-位移曲线。然后用前面理论推导得到的公式(6)去拟合压力-位移曲线，找到比较理想的拟合参数J0，J1，…,JN与τ1，τ2，…,τN，将它们代入公式(4)，得到橡皮布的蠕变函数。数据的具体处理过程如下。

首先用公式(6)对每个点位的压力-位移曲线的数据进行平滑处理，然后对所有平滑处理后的点位数据进行平均处理，最后用公式(6)来拟合均值后获得的压力-位移曲线，确定拟合参数，得到橡皮布的蠕变函数。

从拟合的效果来看，橡皮布A的拟合曲线的均方根误差是0.000 224 1，橡皮布B的拟合曲线的均方根误差是0.001 843。函数表达式(7)是由拟合所得参数确定的橡皮布A的蠕变函数，函数表达式(8)是由拟合所得参数确定的橡皮布B的蠕变函数。图4所示为这两个蠕变函数的图像。

J(t)=298.5+301.5(1-e-t/1.047)+

212.4(1-e-t/1.880)+283.2(1-e-t/0.340)

(7)

J(t)=184.8+396(1-e-t/0.99)+

0.02(1-e-t/1.68)+154.4(1-e-t/1.00)

(8)

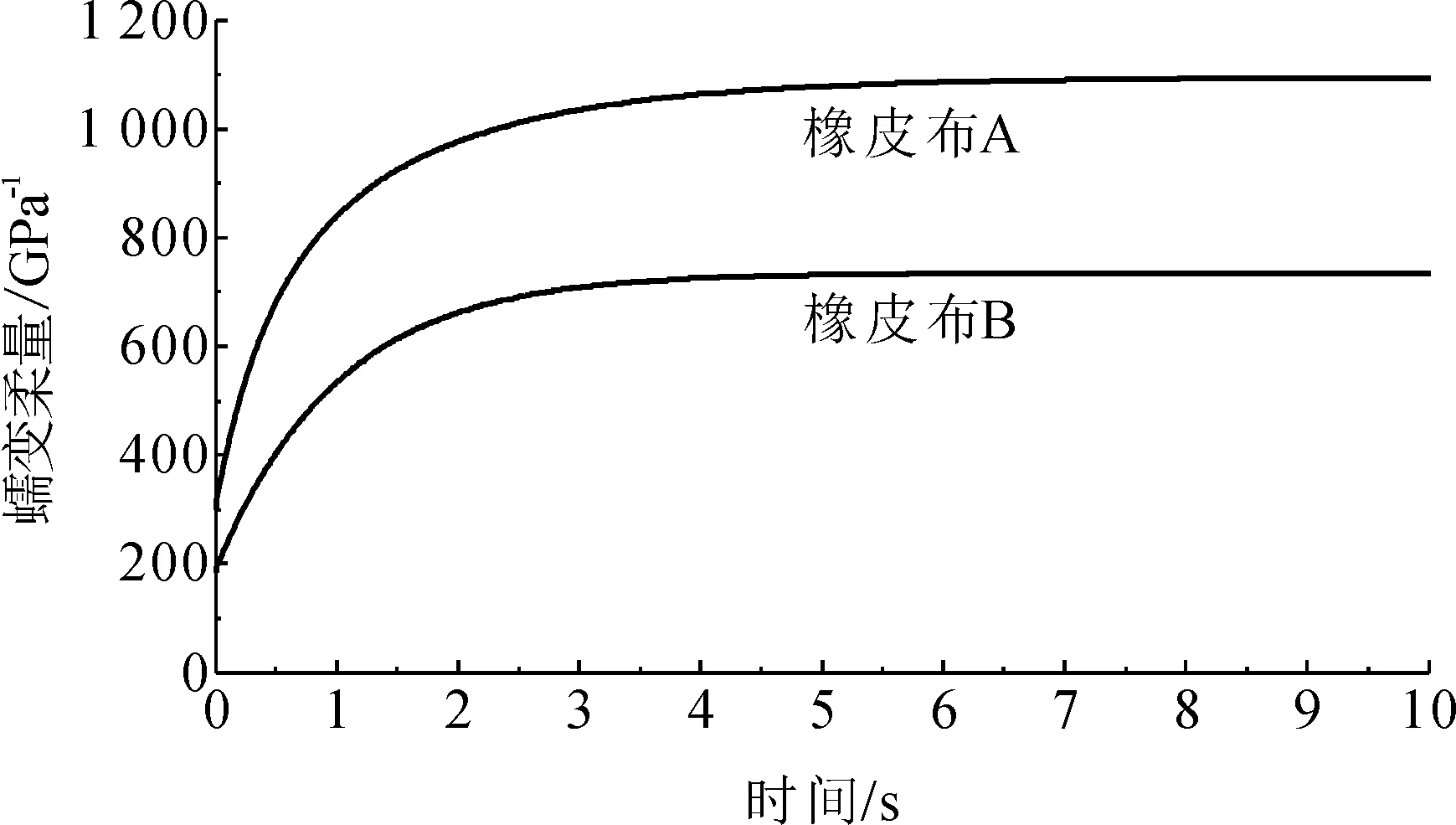
图4 蠕变函数曲线

3 橡皮布蠕变对胶印机油墨传递影响的数值计算

为了研究橡皮布粘弹性对胶印机油墨传递机理的影响，将前文得到的橡皮布蠕变函数引入到胶印机油墨传递的接触理论模型中，进行数值计算。

以弹流润滑理论为基础，以胶印机橡皮滚筒与压印滚筒间的滚压接触为研究对象建立油墨传递的滚压模型。进行必要的理想化假设: 假设油墨为牛顿流体，流体只做层流运动，无涡流及紊流；等温条件(油墨温度为工作环境温度)。建立接触模型的Reynold方程(9)[13]：

(9)

式中p为油膜压力，h为油膜厚度，x为接触区域坐标，η为流体粘度，ρ为流体密度，U为常量。

建立接触模型的载荷平衡方程如下：

(10)

式中,xin、xout分别为油墨滚压接触区域入口、出口处的位置坐标。

建立油墨膜厚方程如下[14]：

(11)

式中,h0为滚筒初始间隙，R为滚筒的当量半径，E′为滚筒的当量弹性模量。

建立等温条件下油墨密度方程如下：

(12)

式中ρ0为环境密度，A、B均为常量。

建立油墨粘度方程如下[15]：

(13)

式中η0为环境粘度，z为粘压系数。

采用多重网格法对模型进行离散和数值计算求解。分两种情况分别进行计算：一种是不考虑橡皮布蠕变行为，将橡皮布作为普通的无时变弹性体来看待实施数值计算；另一种是考虑橡皮布蠕变行为，将前面得到的橡皮布A的蠕变函数表达式(7)应用于数值计算。

图5为计算得到的印刷载荷与印刷速度共同影响下的接触出口处油膜厚度等高线图。对比图5(a)与图5(b)可知：在图5(a)的理想载荷区间(图中虚线所包围区域)，随着印刷速度提高，油膜厚度逐渐变大，而在图5(b)的理想载荷区间内，随着印刷速度提高，油膜厚度逐渐变小。

图5 接触出口处油膜厚度等高线图

而大量的实验数据与使用实践反映出，考虑粘弹性的数值计算结果更加符合胶印机实际传递规律。文献[16]表明油墨转移率随着印刷速度的增加而缓慢减小 。文献[17] 指出：印刷过程中总会由于各种各样的原因不断调节印刷速度,致使印品上的转移墨量不稳定；印刷速度高时密度值下降,反之则大。文献[16]、[17]提及的“油墨转移率”、“(油墨)密度值”在印刷工程领域均是表征印品墨层厚度的概念。“油墨转移率减小”与“密度值下降”均代表“油墨墨层变薄”，这与考虑橡皮布粘弹性时建模、仿真计算的结果是一致的，而与不考虑橡皮布粘弹性行为的仿真计算结果相悖。文献[16]、[17]的研究结果表明考虑橡皮布的粘弹性行为的接触模型能够更加精确地反映油墨的实际传递规律。

4 结 论

在理论分析与纳米压痕技术实验测试的基础上得到了胶印橡皮布的蠕变函数，将其引入到基于弹流润滑理论的胶印机油墨传递接触模型中，采用数值计算的方法研究了印刷橡皮布的粘弹性蠕变行为对胶印机油墨传递机理的影响。

研究结果表明：在胶印机油墨传递精确机理的研究中，橡皮布的粘弹性蠕变行为不可忽视。研究胶印机油墨传递的精确机理，只有依靠理论模型的精细化，才能做到承印物油墨量预测的精确化，才能突破胶印机发展瓶颈，不断提高胶印机的自动化与智能化水平。

参考文献：

[1] Heidelberger Druckmaschinen A G. 100 years of offset printing: innovations, markets, technology[EB/OL]. 2013[2013-07-05]. http://www.docstoc.com/docs/159679082/Years-of-Offset-Printing-Heidelberg.

[2] Helmut Kipphan. Handbook of print media: technologies and production methods[M]. New York: Springer, 2006.

[3] 席瑛，曹从军，夏卫民. 胶印油墨铺展过程的Fluent模拟[J]. 西安理工大学学报, 2013,29(3):343-346.

Xi Ying, Cao Congjun，Xia Weimin. Simulation of ink spreading process of offset printing by Fluent[J]. Journal of Xi’an University of Technology, 2013,29(3):343-346.

[4] 中华人民共和国工业和信息化部. 产业关键共性技术发展指南(2013)[EB/OL]. 2013[2013-09-16]. http://www.miit.gov.cn/n11293472/n11293832/n11293907/n11368223/15626934.html,2013.

[5] 余节约.胶印油墨预置机制与技术的研究[D]．南京：南京林业大学，2012.

Yu Jieyue. Study on the mechanism and technology of offset printing ink preset[D]. Nanjing: Nanjing Forestry University，2012.

[6] 李文育，张二虎，于佳，等. 基于机器视觉的印刷图像色彩在线检测系统设计[J].西安理工大学学报, 2013,29(2): 159-164.

Li Wenyu，Zhang Erhu，Yu Jia，et al. The design of online detection system for printing image color based on machine vision[J]. Journal of Xi’an University of Technology,2013,29(2): 159-164.

[7] Scaraggi M, Persson B N J. Theory of viscoelastic lubrication[J]. Tribology International, 2014,72:118-130.

[8] 洪磊．基于纳米压痕技术与有限元法的粘弹性材料力学特性研究[D]．合肥：安徽大学，2011.

Hong Lei. Research on mechanical characteristic of visco-elastic materials by nano-indentation and FEM[D]. Hefei: Anhui University，2011.

[9] Yu Hualong, Li Zhe, Wang Q Jane. Viscoelastic-adhesive contact modeling: application to the characterization of the viscoelastic behavior of materials[J]. Mechanics of Materials, 2013, 60: 55-65.

[10] Sneddon I N. The relation between load and penetration in the axisymmetic boussinesq problem for a punch of arbitrary profile[J]. International Journal of Engineering and Science, 1965,3:47-57.

[11] Lee E H, Radok J R M. A critical appraisal of the extraction of creep parameters from nanoindentation data obtained at room temperature[J]. Acta Materialia, 2006, 54: 5489-5499.

[12] 何曼君，张红东，陈维孝，等．高分子物理[M]．上海：复旦大学出版社，2006.

[13] 温诗铸，黄平．摩擦学原理[M]．北京：清华大学出版社，2002.

[14] 杨沛然．流体润滑数值分析[M]．北京：国防工业出版社，1998.

[15] 温诗铸，杨沛然．弹性流体动力润滑[M]．北京：清华大学出版社，1992.

[16] 冯长勇．胶印油墨转移的应用研究[D]．西安：西安理工大学，2007.

Feng Changyong. Study on application of offset printing’s ink transfer [D]. Xi’an: Xi’an University of Technology，2007.

[17] 冷彩凤．印刷速度与印刷质量关系的研究[J]．包装工程，2008，29(5):193-194.

Leng Caifeng. Research on printing speed and printing quantity[J]. Packaging Engineering，2008，29(5):193-194.