基于滑模变结构的轮式移动机器人Leader-Follower编队控制
2014-03-27杨延西张浩辛志波
杨延西,张浩,辛志波
(西安理工大学 自动化与信息工程学院,陕西 西安 710048)
在多移动机器人领域编队控制是最重要的,近年来越来越多的学者投身于研究编队控制中。文献[1]研究了近几年单个智能车轨迹跟踪控制算法,并做实验验证反馈线性化和动态反馈线性化控制方法。文献[2]~[18]采用控制,控制算法采用反馈线性化,并扩展到多移动机器人系统中。文献[3]研究了神经网络输出反馈控制。文献[5]提出了将模糊控制与Backstepping相结合进行控制编队,而文献[5]是应用虚结构方法控制队形,主要思想是虚拟一辆智能车,其他车辆跟随这一虚拟车辆。文献[6]中移动机器人之间通信,并应用Backstepping控制方法控制编队队形。文献[7]应用经典PID控制。文献[16]应用滑模变结构控制方法控制机器人编队,文献[17]分别应用反馈线性化和滑模变结构两种控制算法,并对比了两种方法的控制效果。文献[18]基于视觉传感器实现反馈线性化和滑模变结构两种控制算法。
综合国内外相关研究发现应用较多的控制方法为反馈线性化,反馈线性化的基本思想是通过反馈把非线性系统变为线性系统。但模型中有干扰时,反馈线性化并不能达到控制要求,而滑模变结构控制抗干扰能力较强,但由于编队控制模型的控制输入参数是非线性的,仅应用滑模变结构控制其变换过程较为复杂,且根据参考文献[16]和[17]可知,系统的响应速度慢,所以本研究结合反馈线性化和滑模变结构控制,对移动机器人运动学模型进行控制,仿真结果表明本控制方法既增加了系统的鲁棒性又增加了系统的动态响应。
1 移动机器人编队
1.1 基于Leader-Follower编队模型
本研究以两移动机器人为例,建立运动学编队模型,如图1所示,Ri和Rj代表两个移动机器人,下标i、j为两机器人编号,设其中Ri为Leader,其位姿为xi,yi,θi;Rj为Follower,其位姿为xj,yj,θj。Lij为机器人间距,φij为Leader速度方向与Lij之间的相对夹角,d为万向轮到驱动轮的垂直距离。

图1 Leader-Follower模型
由图1易知V、W分别为合速度方向、合角速度方向。可以得到LeaderRi的运动学模型为:
(1)
FollowerRi的运动学模型为:
(2)
式中,vi、vj分别为Leader、Follower的线速度,ωi、ωj分别为Leader、Follower的角速度;γ=βij+ψij,βij=θi-θj。
1.2 反馈线性化控制[2]
本研究指定Leader的运动轨迹,所以本研究主要控制移动机器人队形,由公式(2)可以看出,编队控制模型是非线性系统,反馈线性化成为控制此模型较有效的控制方法,反馈线性化主要思想是把一个非线性系统转化成为一个线性系统,从而应用线性系统的方法来解决非线性系统的问题。以文献[2]为例来说明,文献[2]将运动学模型转换为矩阵表达式形式,即:
(3)
其中,qij为系统输出,uj为机器人Rj的输入,ui为机器人Ri的输入。相关表达式列示为:
qij=[Lijψij]T
uj=[vjωj]T
ui=[viωi]T
通过反馈线性化,Follower控制输入uj为:
uj=A-1(e-Bui)
(4)
其中,e为辅助控制输入,给定为:
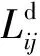
(5)
文献中已给出证明,这里不再赘述。在理想情况下,反馈线性化控制可以达到满意的效果。但当系统存在扰动时,仅简单应用反馈线性化不能确保系统鲁棒性。本研究提出采用反馈线性化和滑模控制结合的方法,增加系统的鲁棒性。
1.3 基于反馈线性化的滑模变结构控制
滑模变结构控制与常规控制的根本区别在于控制的不连续性,即一种使系统“结构”随时间变化的开关特性。该控制特性可以迫使系统在一定特性下沿规定的状态轨迹做小幅度、高频的上下运动,也就是所谓的滑动模态或“滑模”运动。这种滑动模态是可以设计的,且与系统的参数及扰动有关。这样,处于滑模运动的系统就具有很好的鲁棒性。

从理论角度,由于滑动模态可以按需要设计,而且系统的滑模运动与控制对象的参数变化和系统的外干扰无关,一次滑模变结构控制系统的鲁棒性要比一般常规的连续系统强。然而,滑模变结构控制在本质上的不连续开关特性将会引起系统抖振。实际上,抖振是必然存在的,而且消除了抖振也就消除了变结构控制的抗扰动能力,因此,消除抖振是不可能的,只能在一定程度上削弱。本研究中,采用饱和函数代替符号函数,可大大减弱抖动。饱和函数为:
(6)
参数δ影响控制量,δ如果太大,就会削弱滑模函数的作用,δ如果太小,饱和函数有可能达不到减小抖振的效果。所以仿真中δ应取较小的正数。
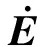
由于系统为一阶系统,滑模函数设计为:
(7)
其中,c1>0、c2>0。
设计控制器为:
uj=A-1(α-Bui)
(8)
式中:
其中c=[c1c2], sat(·)为饱和函数,pinv(·)代表求矩阵c的广义逆。
证明:定义Lyapunov函数为:
(9)
并将uj带入,则有:
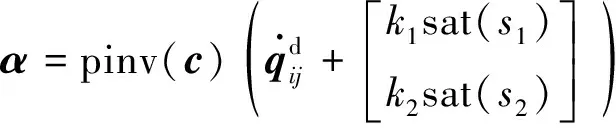
(10)
其中,

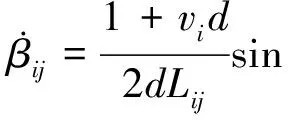
2 仿真结果
本研究仿真主要分为三个部分,第一部分验证本方法的正确性,第二部分讨论本方法的抗干扰性,第三部分将本算法加入硬件智能车平台。
2.1 本研究方法的正确性

编队模型为:
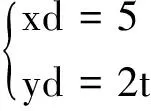
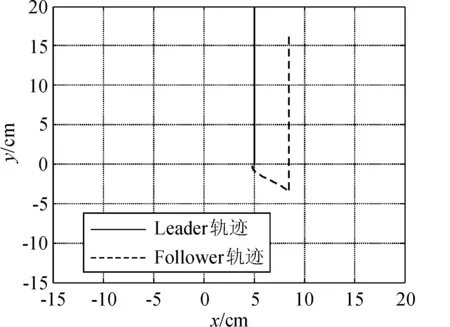
图2 移动机器人的线形轨迹
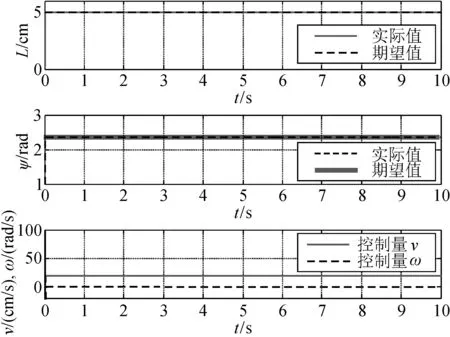
图3 模型状态及控制输出
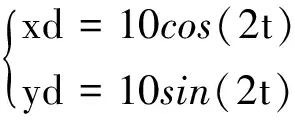
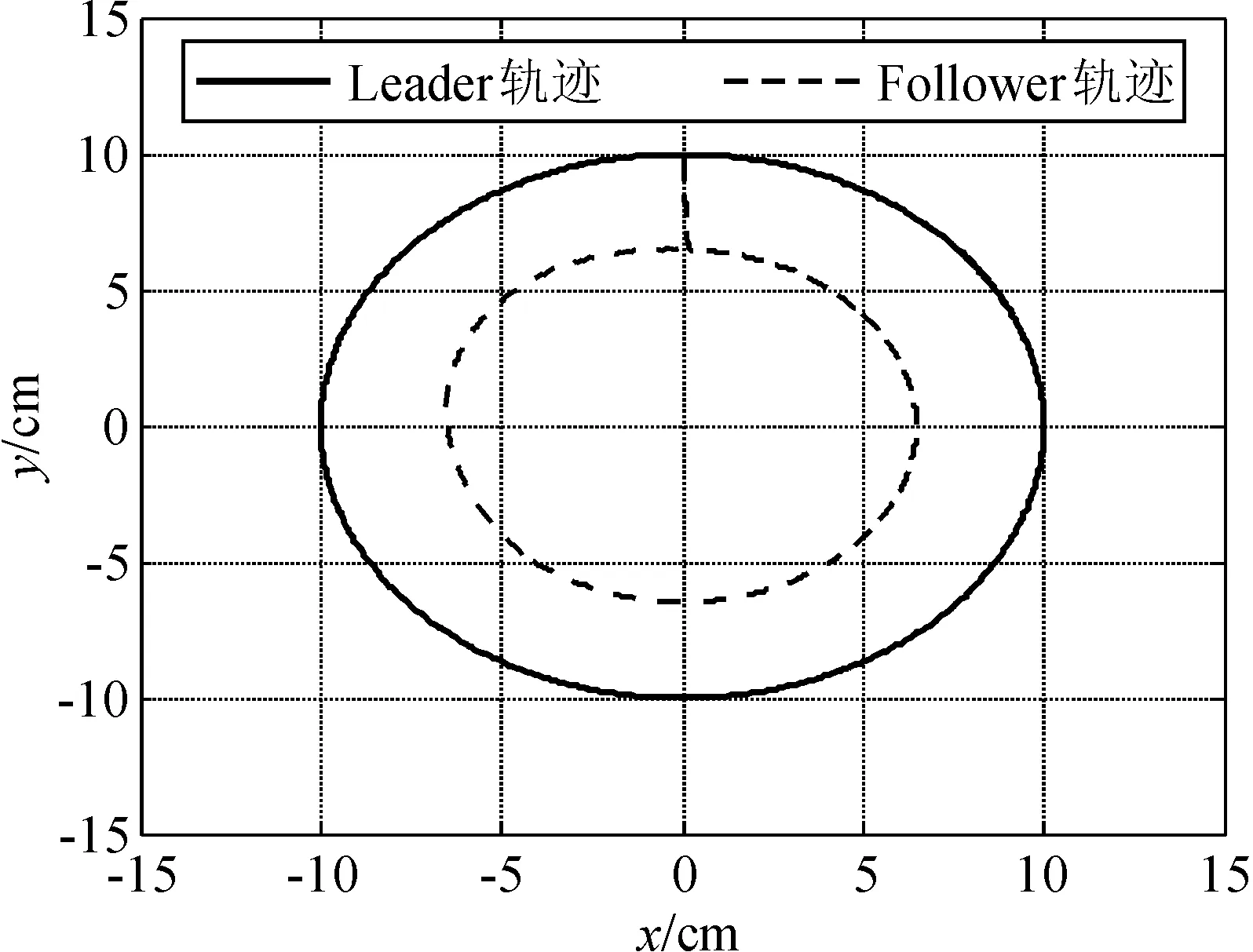
图4 移动机器人的圆形轨迹

图5 基于反馈线性化的滑模变结构控制
假定系统无干扰、系统模型准确,仿真结果表明无论是线性编队还是圆形编队本方法都可以有效控制并快速稳定在给定值。图5(a)采用符号函数,控制输出呈现高频振荡。为使系统稳定,控制量高速震荡,因为本系统要控制移动机器人直流电机,控制输出的高频震动会损坏电机,为消除高频震动,图5(b)采用饱和函数代替符号函数,控制输出抖振基本消除。

图6 三个机器人圆形编队估计

图7 跟随机器人模型状态及控制输出
由以上仿真可知,编队控制适用于多个移动机器人同时跟随领航机器人。这样就扩展为多移动机器人编队控制。
通过上面3个仿真结果,与文献[16]相比,本研究基于反馈线性化的滑模变结构控制算法提高了系统的动态响应,同时提高了系统的鲁棒性。
2.2 本研究方法的抗干扰性能

1)当存在系统扰动时,即模型为:
其中,d(t)=[5sin(2t); 5cos(2t)]为系统扰动。反馈线性化参数值为k1=50,k2=10,本方法参数值为k1=1.2,k2=1.2,c1=0.001,c2=0.001,δ1=0.0015,δ2=0.0009,两种控制仿真如图8及图9所示。

图8 反馈线性化控制结果

图9 基于反馈线性化的滑模变结构控制
仿真结果表明,当系统模型存在干扰时,如图8所示,反馈线性化控制效果明显变差,不能达到控制要求,而本控制方法如图9,系统无稳态误差,但控制输出存在一定的抖振,因为是采用滑模变结构控制,所以完全消除抖动也就消除了系统的抗干扰能力。
2)当控制输入存在扰动时,即:
uj=uj+Δ
其中,Δ是均值为15,方差为0.5的随机数向量,即:
反馈线性化参数值为k1=40,k2=20,本研究方法参数值为k1=1,k2=1,c1=0.002,c2=0.0015,δ1=0.0015,δ2=0.001,仿真结果如图10及图11所示。
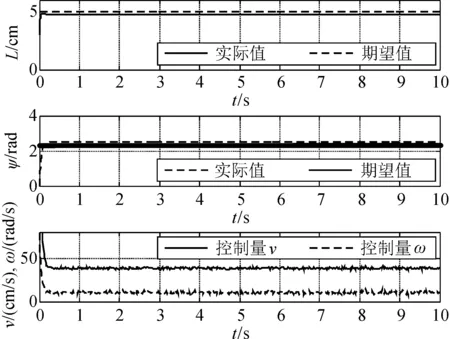
图10 反馈线性化控制结果

图11 基于反馈线性化的滑模变结构控制
图10仿真结果表明,当系统控制输入加入噪声时,系统存在稳态误差,而图11中,本研究方法可以快速达到给定值且不存在稳态误差。
2.3 硬件平台验证本文算法
本研究在室内进行两个智能车编队试验,试验环境选择空旷的实验室,即试验场地不存在障碍。试验周围环境可以是任意的,由于本研究将颜色空间转换到HSV空间中,并选择红色作为识别颜色,所以背景中有其他颜色可以直接滤掉。自制智能车速度的最大值为400 mm/s,驱动轮与万向轮间距d=115 mm,为加快智能车处理图像速度,智能车摄像头输出160×120大小图像,平均每秒可以处理10帧左右图像数据,数据图像不稳定的主要原因是背景复杂度不一样,背景简单时处理速度快,相应地,背景复杂时处理速度偏慢。


图12 两辆智能车实验结果


图13 三辆智能车实验结果
实验结果表明,本算法可以用于实际中传感器较少的智能车控制。该算法相对于传统滑模控制算法相对稳定,在编队控制中能达到控制要求,并在传感器较少且低控制主频的硬件平台中简单实现。
3 结 论
1)对于智能机器人编队系统采用反馈线性化控制,在模型存在干扰的情况下,不能达到控制要求;而仅采用滑模变结构控制方法,系统的响应速度慢,并且变换过程较为复杂。本研究提出结合反馈线性化和滑模变结构控制,对移动机器人运动学模型l-φ进行控制,仿真结果表明,本研究控制方法既增加了系统的鲁棒性又增加了系统的动态响应。
2)为消弱滑动模态的抖振,控制律中用饱和函数替换了符号函数。
3)在硬件平台传感器较少的条件下,实现了简单的小车直线编队,并取得了比较稳定的效果。
参考文献:
[1] Luca A D, Oriolo G, Vendittelli M. Control of wheeled mobile robots: an experimental overview[J]. Lecture Notes in Control and Information Sciences, 2001,270: 181-226.
[2] Aveek K, Fierro R. A vision-based formation control framework[J]. IEEE Transactions on Robotics and Automation, 2002, 18: 813-825.
[3] Dierks T, Jagannathan S. Neural network output feedback control of robot formations[J]. IEEE Transactions on Systems, Man, and Cybernetics—Part B: Cybernetics, 2010,40: 383-399.
[4] Wu Kongyi, Huo W. Backstepping-based direct adaptive fuzzy formation control of uncertain mobile robots [C]//2010 8th IEEE international conference on control and automation, Xiamen:China, 2010: 9-11.
[5] Ghommam J, Mehrjerdi H, Saa M. Leader-follower based formation control of nonholonomic robots using the virtual vehicle approach [C]//Proceedings of the 2011 IEEE International Conference on Mechatronics, Istanbul, Turkey, 2011: 13-15.
[6] Wang Zhuping, Mao Ying, Chen Guangmou, et al. Leader-follower and communication based formation control of multi-robots [C]//Proceedings of the 10th World Congress on Intelligent Control and Automation , Beijing, 2012: 6-8.
[7] Choi I S, Choij S, Chung W J. Leader-follower formation control without information of heading angle [C]//IEEE/SICE International Symposium on System Integration (SII)Kyushu University, Fukuoka, Japan, 2012: 16-18.
[8] Wu Lijuan, Wang Hui. Multi-robot formation control and simulation [C]//2013 25th Chinese Control and Decision Conference (CCDC), Beijing, 2013: 25-27.
[9] 刘金琨. 滑模变结构控制MATLAB仿真 [M] . 北京:清华大学出版,2012.
[10] 程代展.应用非线性控制[M].北京,机械工业出版社,北京,2006.
[11] Emrani S, Dirafzoon A. Talebi H A. Leader-follower formation control of autonomous underwater vehicles with limited communications[J]. Control Applications (CCA), 2011 IEEE International Conference on USA ,2011: 921-926.
[12] Wang Can. Formation control of multiple robot systems with motion synchronization concept[D]. Hong Kong, City University of Hong Kong,2009.
[13] Chen Jian. Multi-robot formation control: a receding-horizon leader-follower framework[D]. Hong Kong, City University of Hong Kong, 2009.
[14] Golkar M A. Trajectory tracking and formation control of a platoon of mobile robots[D]. Canada, Concordia University.
[15] lyas Eker. Sliding mode control with PID sliding surface and experimental application to an electromechanical plant [J]. ISA Transactions, 2006: 109-118.
[16] 俞辉,王永骥.非完整移动机器人编队的滑模控制[J],机器人,2006 ,28(4):428-432.
Yu Hui, Wang Yongji. Sliding mode control for nonholonomic mobile robot formation[J]. Robot, 2006 , 28(4):428-432.
[17] 黄小起.多移动机器人编队控制的研究[D].沈阳:东北大学,2009.
Huang Xiaoqi. Research on formation control for multiple mobile robots[D]. Shenyang: Northeastern University, 2009.
[18] 贾晓燕.基于视觉的移动机器人编队控制[D].沈阳:沈阳航空航天大学, 沈阳,2011.
Jia Xiaoyan. Formation control of mobile robots based on visual servo[D]. Shenyang: Shenyang Aerospace University,Shenyang,2011.
[19] 张金学,掌名.非完整机器人Leader-Follower编队控制器设计[J]. 智能计算机与应用,2011,1(4):20-22.
Zhang Jinxue, Zhang ming. Design of leader-follower formation controller for nonholonomic mobile robots[J]. Intelligent Computer and Applications,2011,1(4):20-22.
[20] 俞志英,郭戈,钱方.新的基于反馈线性化的车辆编队控制[J]. 大连海事大学学报,2013,39(1):123-127.
Yu Zhiying, Guo Yi,Qian Fang. Novel vehicle formation control based on input-output feedback linearization[J]. Journal of Dalian Maritime University,2013,39(1):123-127.
