直拉法硅晶体生长中单晶炉坩埚内熔体的数值模拟
2014-03-27弋英民张潼刘丹
弋英民,张潼,刘丹
(西安理工大学 自动化与信息工程学院,陕西 西安 710048)
大尺寸、高品质硅单晶是制造微细纳米级集成电路芯片的关键材料,目前我国全部依赖进口。硅单晶炉作为生长电子级硅单晶材料的主要设备,其工艺复杂,技术集成度高,实现困难,在集成电路生产流程中处于首要地位。因此,针对制备单晶硅的各种基础研究和仿真模拟成为了学者们研究的热点。单晶硅按生长方法分有直拉法和区熔法等[1],直拉法也称CZ法,目前广泛应用于晶体制造领域。在CZ法制备单晶硅的过程中,影响晶体质量的因素有坩埚内的硅熔体流动[2]、熔体内杂质分布[3]以及晶体生长面弯月面的形状[4]等。使用计算机模拟晶体的生长环境在晶体制备的仿真中起到了重要的作用,为了衡量仿真算法的正确性,文献[5]提出了Wheeler标准问题,Wheeler标准问题是验证仿真算法正确与否的检验标准。
为了能够模拟晶体的生长情况,一般采用专用软件或者编程实现。文献[6]和[7]采用FEMAG-CZ对单晶炉内的热场和氧浓度分布进行了模拟;文献[8]采用CGSIM对晶体中的微缺陷进行了模拟研究;文献[9]使用Fortran编程,利用Petrov-Galerkin有限元法实现了不同物性参数对晶体生长的影响的模拟;文献[10]也使用通用编程软件,模拟了晶体的生长过程,并通过了Wheeler标准的验证。然而,专用软件需要大量的授权费用,使用通用软件编程需要较高的编程功底和理论水平,因此本文研究使用通用的有限元软件来实现晶体生长相关的数值模拟。
本文采用Fluent 6.3,利用有限容积法结合三阶迎风QUICK离散格式模拟了单晶炉中坩埚内熔体的流场和热场,并用Wheeler标准检验了算法的有效性。对坩埚直径为600 mm的熔体进行了自然对流下的流场、热场以及杂质场的数值模拟。
1 数值模型和物性参数
直拉法晶体生长的简化结构如图1所示。

图1 晶体生长结构简化图
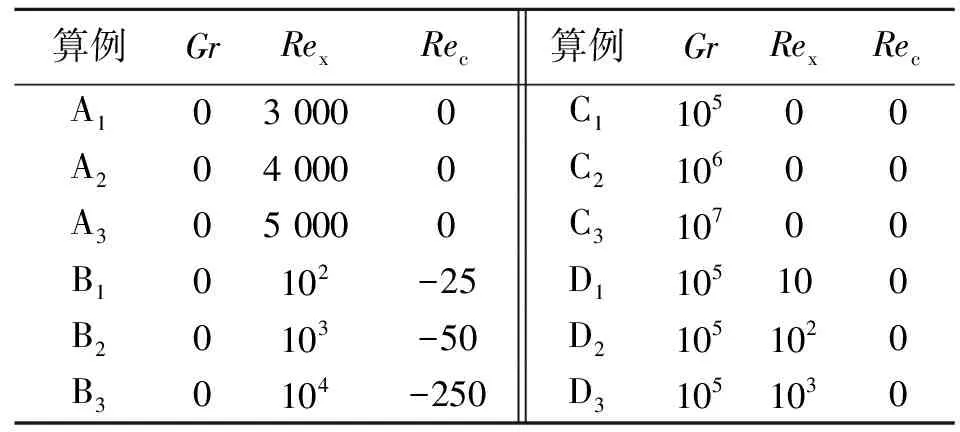
假设坩埚和晶体为同轴圆柱,坩埚半径为Rc,坩埚角速度为Ωc,坩埚内熔体高度为H,晶体半径为Rx(Rx 模拟中假定:①晶体等径生长;②熔体流动和换热是轴对称的;③熔体与晶体界面的自由表面为平面;④忽略熔体自由表面张力和旋转时界面的变化;⑤熔体为轴对称的不可压缩的牛顿流体;⑥不考虑磁场;⑦熔体内的流动为层流;⑧坩埚和生长界面处的流动满足无滑移条件,浮升力满足Bousinesq假设。除密度外,其它物性参数均为常数,熔体的流动和传热满足N-S方程和能量方程。 该模型引入无量纲变量: (1) 式中带*标的变量为有量纲变量,(r,z)为质点坐标;u、v、w分别为质点的轴向速度、径向速度和周向速度;p为压力,T为温度;μ为熔体的粘性系数;ρ为熔体密度;g为重力加速度。 基于之前的假设,无量纲的控制方程为: (2) (3) (4) (5) (6) 本文所采用熔体模型的边界条件为: (7) 相应的,模型中的无量纲参数定义如下: (8) 式中,α为熔体高度与半径之比;β为晶体与熔体半径之比;Pr为普朗特数;Gr为格拉斯霍夫数;Rex和Rec分别是因晶体和坩埚旋转产生的雷诺数。 仿真中采用的硅熔体的物性参数如表1所示[10]。 表1 物性参数表 在1989年召开的北约晶体生长计算模拟大会上,大会主席Wheeler提出了四个测试问题,即Wheeler标准问题。这些标准问题包括四组情况:A组只考虑晶体旋转;B组考虑晶体和坩埚共同旋转;C组只考虑自然对流,晶体坩埚不旋转;D组考虑自然对流和晶体旋转,坩埚不旋转。每组又分三个不同的算例,Wheeler标准问题的参数如表2所示。本文计算了表2中的12组算例。 表2 Wheeler标准问题参数 本文使用Fluent 6.3[11]进行数值模拟,采用层流模型,压力和速度的解耦合用Fluent 6.3中的SIMPLE算法,扩散项差分采用二阶截差中心差分格式,对流项差分采用三阶截差QUICK格式,压力插值采用PRESTO!格式。对Wheeler标准问题的12个算例进行了数值模拟。 算例A结果的流函数如图2所示。在这组算例中,熔体内部只有一个由晶体旋转产生的一个顺时针的涡,熔体沿轴线向上运动,直至晶体边界,然后流向坩埚侧壁,晶体附近的流体由于粘性的作用和晶体一起旋转,产生从轴心指向坩埚壁的离心力,在离心力的作用下,熔体流向坩埚壁,遇到坩埚壁阻挡,被迫下流。转速将涡流的中心移向坩埚侧壁,偏向右上角,并发生形变。同时,速度最快的区域从左上角移至右下角,速度最小的区域在左下角扩大。 图2 算例A的流函数图 在本组算例中,随着晶体转动速度的增加,流函数变大,这说明涡流强度增加。算例A1、A2、A3的流函数最大值分别为8.79E-5、1.18E-4、1.47E-4。 算例B结果的流函数如图3所示。在算例B中,熔体内部出现两个方向相反的涡流,左上角的顺时针涡流是由晶体旋转形成的,右下角的逆时针涡流是由坩埚旋转造成的;随着晶体旋转速度和坩埚旋转速度的同时增大,虽然晶体转速远大于坩埚转速,但是右下角的涡流仍主导着整个流场;晶体生长的理想条件是熔体区域只有一个涡流,显然,这样的情况是不利于晶体生长的。 图3 算例B的流函数图 在本组算例中,随着晶体转动速度和坩埚转动速度的增加,流函数变大,说明涡流强度显著增加。算例B1、B2、B3的流函数最大值分别为8.25E-7、1.86E-6、3.92E-5。加入晶体和坩埚旋转是为了平衡自然对流产生的涡流,但晶体和坩埚的转速过大,产生的涡流强度过大,也对晶体等径生长带来扰动,因此晶体和坩埚的转速应控制在一定范围之内。 算例C中只有浮升力引起的自然对流,熔体内部由一个逆时针的涡占据,随着Gr数的增大,涡流也在变大,最大速度移向坩埚侧壁,涡流的中心几乎没有移动位置。算例C结果的流函数图如图4所示。Gr数在108时,层流模型无法得到收敛的解,证明层流模型不适用,Gr数在108以上的数量级时,应该使用湍流模型。 图4 算例C的流函数图 算例D结果的流函数图如图5所示。算例D相比算例C加上了晶体旋转,结果加上晶体旋转的自然对流和只有自然对流的情况,流函数不管是在形状上,还是在数值上都没有什么变化,和C组的几乎一样。 图5 算例D的流函数图 通过Wheeler标准问题检验后,证明此方法可用,于是,本文将此方法应用于大直径硅晶体,对坩埚半径为300 mm内的硅熔体,进行自然对流下的流场、热场和氧浓度的数值模拟。熔体高度与半径之比α=0.6;晶体与熔体半径之比β=0.4。 图6为坩埚半径为300 mm时,硅熔体在自然对流下的流函数图。可以看出,流函数的基本形状和层流模型的基本相同,是充满整个熔体区域的一个逆时针大涡,但是涡心更偏向坩埚侧壁,此涡是由于坩埚底部和侧壁的温度比熔体高,坩埚壁附近区域的熔体受热后,密度变小,在浮升力的作用下,沿着侧壁上升,然后在自由表面和生长界面处受冷,密度变大,下沉至坩埚底部,从而形成完整的涡流。 图6 硅熔体流函数图 图7为坩埚半径为300 mm时,硅熔体在自然对流下的等温图。低缺陷晶体生长的温度条件是在整个晶体生长过程中固液交界面保持平坦,这要求等温线近似垂直于生长方向,即等温线比较平坦。图7中,靠近晶体生长面的等温线比较平坦,随着远离晶体生长界面,等温线变得更为陡峭。自然对流的湍流会加剧温度的波动,而温度的波动是产生生长条纹的重要原因,因此要获得高品质单晶硅,控制其温度波动是关键。 图7 硅熔体等温图 图8显示的是在自然对流作用下坩埚半径为300 mm的硅熔体中的氧原子浓度分布图。可以看出,在熔体内部的大部分区域,氧原子浓度都很小。并且,由于涡流在自然对流的作用下,沿坩埚壁经由自由表面再流向对称轴中心,因此一部分氧杂质也会从自由表面挥发出去,在图中就可以看出大部分的氧杂质聚集在坩埚底部和侧壁。如果熔体内的流动加强,那么氧原子杂质有可能会来不及挥发而被带入熔体,从而形成熔体内的杂质,因此抑制自然对流的流动强度对降低熔体内的氧杂质至关重要。 图8 硅熔体氧浓度图 根据本研究结论,通过在直径300 mm硅单晶炉修改拉晶的SOP表有关参数,进行不同SOP温度参数下的拉晶实验如图9所示。 图9 在不同拉晶SOP参数下的晶棒 由图9可以看出,在晶体生长界面处温度波动大,会导致生长处的晶体无法成晶,甚至断裂。而当控制晶体生长界面(弯月面)温度为硅熔体成晶温度1 420℃±0.1℃时,可以长出完美的硅单晶。 本文通过Fluent6.3对Wheeler标准问题中的12个算例进行了数值计算,结果表明,使用Fluent计算的结果与文献[10]中的基本一致。本文的仿真实验结果表明,对于直径600 mm坩埚必须控制合适的晶转和埚转范围,以保证晶体生长,控制温度的波动可以抑制生长条纹,抑制自然对流的可以降低熔体内的氧杂质含量。本研究下一步将在自然对流下增加晶体和坩埚旋转,并增加间壁对氧浓度的抑制方面的研究。 参考文献: [1] 蒋荣华,肖顺珍. 半导体硅材料的进展与发展趋势[J].四川有色金属, 2000,3:1-7. Jiang Ronghua,Xiao Shunzhen. Progress and development trend of semiconductor Si materials[J]. Sichuan Nonferrous Metals,2000,3:1-7. [2] 宇慧平,隋允康,张峰翊,等. 紊流模型模拟分析旋转对提拉大直径单晶硅的影响[J]. 人工晶体学报, 2004,33(5): 835-840. Yu Huiping,Sui Yunkang,Zhang Fengyi, et al. Numerical simulation on the effect of rotation in a czochralski silicon crystal growth with a turbulence model[J]. Journal of Synthetic Crystal, 2004,33(5): 835-840. [3] Ren Bingyan,Zhao Long,Zhao Xiuling, et al. Effects of argon gas flow rate and guide shell on oxygen concentration in czochralski silicon growth [J]. Rare Metals, 2006, 25(1): 7-10. [4] 滕冉,戴小林,肖清华,等. 大直径硅单晶生长过程中固/液界面形状及熔体流动的数值分析[J]. 人工晶体学报,2013,42(4): 611-615. Teng Ran,Dai Xiaolin,Xiao Qinghua, et al. Numerical simulation of melt/crystal interface and melt flow during large diameter single silicon crystal growth[J]. Journal of Synthetic Crystal, 2013,42(4): 611-615. [5] Wheeler A A. Four test problems for the numerical simulation of flow in czochraski crystal growth [J]. Journal of Crystal Growth,1990,102(4):691-695. [6] 王庆,张婷曼. 基于FEMAG-CZ热场仿真软件的单晶炉热场分析[J]. 计算机光盘软件与应用, 2011,17: 65-66. Wang Qing,Zhang Tingman. Single crystal furnace thermal field analysis on FEMAG-CZ thermal field simulation software[J]. Computer CD Software and Applications, 2011,17: 65-66. [7] 常麟,周旗钢,戴小林,等. CUSP磁场对直拉硅单晶氧浓度分布影响的数值模拟[J].稀有金属,2011,35(6): 909-915. Chang Lin,Zhou Qigang,Dai Xiaolin, et al. Numerical simulation of CUSP magnetic field on oxygen concentration distribution in CZ-Si crystal growth[J]. Chinese Journal of Rare Metals, 2011,35(6): 909-915. [8] 曾庆凯,关小军,潘忠奔,等. Ф400mm直拉硅单晶生长过程中氧浓度对微缺陷影响的数值模拟[J]. 人工晶体学报,2011,40(5):1150-1156. Zeng Qingkai,Guan Xiaojun,Pan Zhongben, et al. Simulation of microdefect with different oxygen concentration in Ф400 mm CZ silicon crystal growth[J]. Journal of Synthetic Crystal,2011,40(5): 1150-1156. [9] 李友荣,魏东海,余长军,等. 物性参数对硅单晶Czochralski生长过程的影响[J]. 热科学与技术,2006,5(4): 351-355. Li Yourong,Wei Donghai,Yu Changjun, et al. Effects of thermophysical properties on silicon single crystal czochraski growth processes[J]. Journal of Thermal Science and Technology,2006,5(4): 351-355. [10] 宇慧平. MCZ大直径单晶体生长的数值模拟及控制参数优化[D]. 北京:北京工业大学,2005. Yu Huiping. The numerical simulation of the large diameter MCZ crystal growth and the optimization of the operational parameters[D]. Beijing:Beijing University of Technology,2005. [11] 李国栋,哈岸英,钟小彦,等. 基于FLUENT 的渗流场数值模拟分析[J]. 西安理工大学学报,2011,27(3): 317-320. Li Gudong,Ha Anying,Zhong Xiaoyan, et al. Numerical simulation of seepage field based on FLUENT[J]. Journal of Xi’an University of Technology, 2011,27(3): 317-320.

2 Wheeler标准化问题
3 数值模拟及分析








4 结 论
