全光纤分光转动拉曼测温激光雷达探测性能优化

李仕春，华灯鑫，宋跃辉，石晓菁, 乐静

(西安理工大学 机械与精密仪器工程学院，陕西 西安 710048)

温度是气象学中描述大气状态的重要参数之一，对气象预报、大气物理及气候研究具有重要意义。近几十年来，转动拉曼激光雷达作为强有力的测量大气温度廓线的手段之一，得到了快速发展[1-3]。但是，由于其传统分光系统重量大、调整复杂，限制了转动拉曼激光雷达系统的机载及星载应用。光纤Bragg光栅(FBG)具有良好光谱分光特性，目前已广泛应用于通信及传感领域[4]，国际上已有FBG应用于差分吸收激光雷达的相关研究报道[5]。笔者所在课题组近几年开展了全光纤分光转动拉曼测温激光雷达的相关研究[6-7]，研究全光纤转动拉曼分光系统的可行性，结果表明系统耦合效率和FBG分光特性是该分光系统的关键技术。

本文在实验室现有干涉滤光片分光的拉曼激光雷达系统平台上，结合单模光纤耦合器和FBG分光器等关键光学器件加工工艺水平，针对耦合效率和FBG光谱特性等关键技术问题进行优化分析。由于FBG结构参数加工时连续可调[8]，以激光雷达的统计温度误差为优化目标，构建全光纤分光转动拉曼测温激光雷达的优化数学模型，优化FBG的性能参数和结构参数。利用通信领域空间光与单模光纤耦合的有关研究成果[9]，设计基于GRIN透镜的望远镜耦合系统[10]，仿真分析其近场耦合效率和激光雷达系统性能参数。

1 全光纤分光激光雷达系统

全光纤分光转动拉曼测温激光雷达系统结构如图1所示。系统采用Nd:YAG种子注入激光器作为激励光源，其工作波长为532.25 nm，输出脉冲的能量为300 mJ，重复频率为20 Hz，光斑直径为9 mm，光束发散角为0.5 mrad，激光束经5倍准直扩束后，垂直射入大气，接收系统采用Dall-Kirkham式卡塞格林望远镜，直径为250 mm，将望远镜接收的大气回波信号通过耦合系统接入单模光纤，然后传输给全光纤分光系统，滤出的高低量子数的拉曼信号分别由光电倍增管(PMT)光电转换，经光子计数器统计后输入计算机进行数据处理和温度反演。

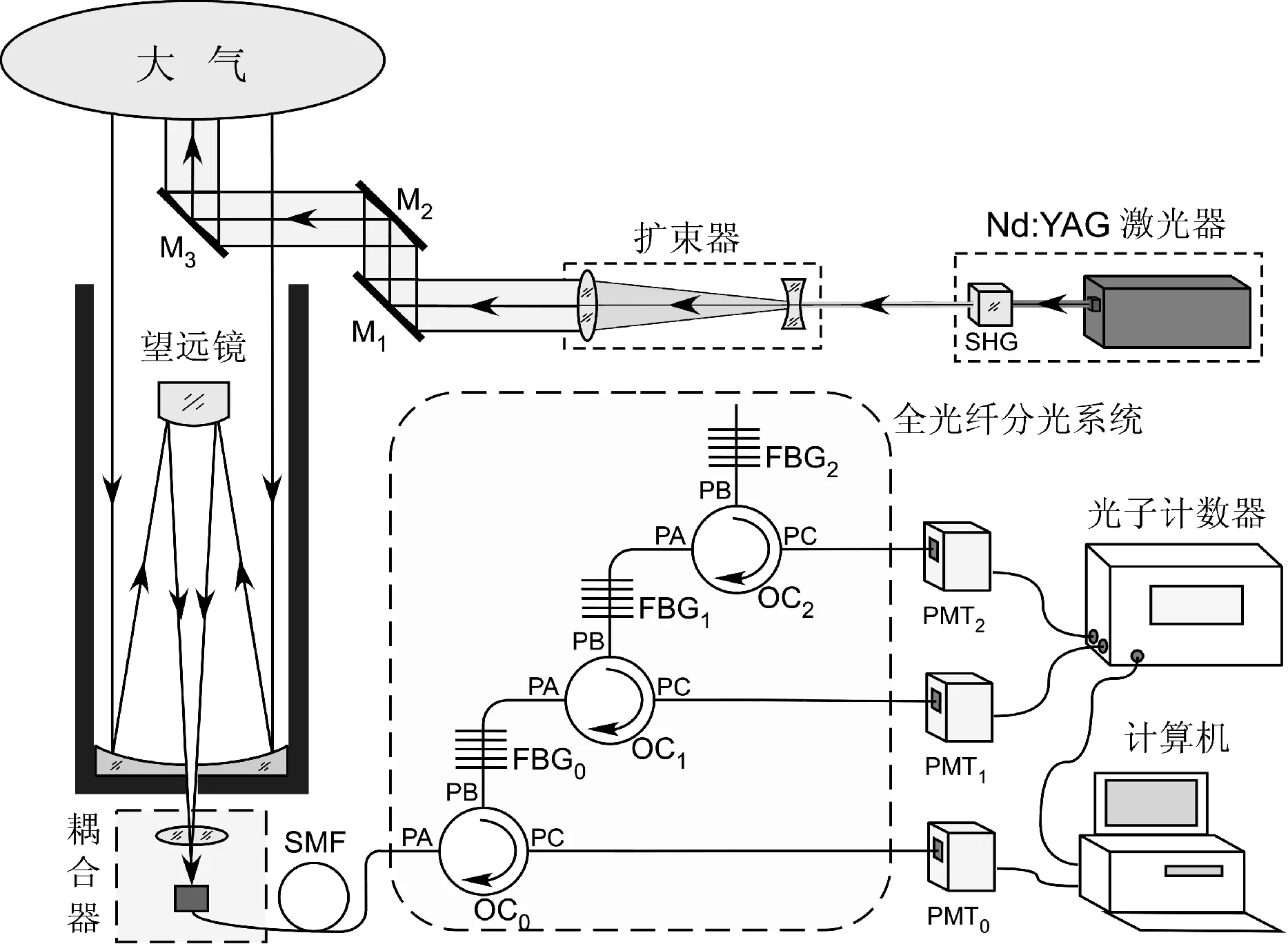
图1 全光纤分光拉曼测温激光雷达系统原理图

2 激光雷达系统优化数学模型

转动拉曼测温激光雷达的工作原理是高低量子数的转动拉曼散射截面对温度的依赖性，即较低量子数的谱线强度随温度升高而降低，而较高量子数的谱线强度随温度升高而增加，故可利用带有温度信息的两个拉曼信号强度比来反演大气温度[1]，通常采用具有高温度灵敏度的转动量子数为6和14的纯转动拉曼谱线进行系统搭建[2-3]。为保证较高的系统输出信噪比，需要分光通道具有一定带宽，但由于附近拉曼谱线的温度灵敏度较低，同样会降低系统测量精度，所以需要综合考虑分光系统中心波长及带宽等参数对温度灵敏度和系统信噪比的影响，进行分光系统关键参数的优化设计。

拉曼测温激光雷达回波信号功率为[1-3]：

(1)

式中，K为系统常数，P0为光源激光脉冲功率，c为光速，Y(z)为系统几何重叠因子，β(z)表示大气分子(主要为N2和O2)的后向散射系数，且β(z)=N(z)·σ，σ为大气分子拉曼后向散射截面，αλT(z)和αλR(z)分别为大气对发射波长λT和接收波长λR的消光系数。

假设高低量子数通道的光谱传输函数分别为HH(λ)和HL(λ)，则同时滤出多条谱线的高低量子数通道的信号强度比可表示为：

(2)

可看出，耦合效率对R(T,z)的影响较小，而高低量子数通道的光谱传输影响较大。为反演大气温度信息，需建立R(T,z)与T(z)之间的数学关系，通常假设具有如下的拟合函数[2]：

R(T,z)=exp[-A·T-2(z)-

B·T-1(z)-C]

(3)

式中，z为探测高度，A、B、C为激光雷达系统常数，可利用无线电探空仪等其它数据进行标定。

为了对系统性能进行优化和评价，需综合考虑系统灵敏度及信噪比，通常定义系统灵敏度为[11]：

(4)

系统的信噪比，即拉曼通道信号强度比R(T,z)的信噪比，依据误差理论，通常可由高低量子数两个转动拉曼通道的信噪比进行合成，即：

(5)

式中，SNRH(z)和SNRL(z)分别为高、低量子数拉曼通道的信噪比。故拉曼激光雷达系统的统计温度误差通常表示为[1,11]：

ET(z)=SNR-1(z)·S-1(z)

(6)

由式(6)可看出，统计温度误差综合了系统的信噪比和灵敏度的影响，本文将该公式作为系统探测性能优化的目标函数。

3 FBG分光系统参数优化设计

激光雷达系统的望远镜，除接收到携带温度信息的转动拉曼信号外，同时也接收到气溶胶产生的米散射和大气分子产生的瑞利散射回波信号，它们可用来反演大气气溶胶的光学特性等，但对于转动拉曼测温激光雷达则是干扰信号，由于转动拉曼散射截面通常比瑞利散射小3～4个数量级，理论计算表明，系统需要对以米散射、瑞利散射等为主的噪声信号提供7个数量级以上的抑制[6-7]，设计的分光系统见图1，本文通过对系统的统计温度误差进行数值分析，优化设计均匀FBG的关键参数，以便搭建更合理的光纤Bragg光栅加工系统。

FBG可看作光纤折射率的一种微扰结构，依据耦合模理论，单模光纤均匀FBG反射率为[8]：

(7)

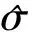
由于切趾FBG加工要求较高，故采用较简单的均匀FBG实现分光系统设计。因FBG两端折射率突变，形成法布里-珀罗(F-P)效应，光栅反射谱两边会产生很多旁瓣，这会降低系统的滤光效果，但是通过使旁瓣峰值与相应拉曼谱线进行匹配，可有选择地让信号和噪声通过，而抑制相邻拉曼谱线间的噪声，提高分光系统的信噪比。不同的FBG参数，可得到不同的FBG反射光谱特性，而FBG的中心波长和半峰值带宽性能参数可综合反映FBG的Bragg波长、平均折射率变化、光栅长度等结构参数。若考虑直接对FBG结构参数进行优化，则优化仿真计算比较复杂，在此采用两级优化方案。首先，以FBG中心波长和半峰值全带宽为参数构建高斯型反射光谱函数，以1.5 km高度处式(6)的统计温度误差为优化目标，对FBG的中心波长和半峰值带宽参数进行优化。然后，以优化后的FBG的中心波长和半峰值带宽为参照，构建FBG结构参数的初始值，再以1.5 km高度处式(6)的统计温度误差为优化目标，对Bragg波长、平均折射率变化、光栅长度等参数进行优化。

由于式(6)的统计温度误差是随高度变化的函数，这不利于进行优化计算，但是理论上该函数通常随高度单调变化，故此处采用某一特定高度(1.5 km)进行优化设计，认为其结果对其它高度成立。另外，因该系统主要用于测量边界层温度，故选用1.5 km高度的统计温度误差作为优化目标进行数值计算(如图2所示)。

图2 FBG中心波长和半峰值带宽优化等高线图

图2(a)表示优化目标误差随FBG1和FBG2中心波长(λ1和λ2)的变化情况，可看出FBG1中心波长在530.5 nm附近的变化梯度较小，而在531.5 nm左右的变化梯度较大，这主要是由于此时FBG1的反射谱比较接近激光发射波长，米散射和瑞利散射信号增加较快导致的，而FBG2由于距离激光发射波长较远，两个方向的变化梯度相差不大。

图2(b)表示优化目标误差随FBG1和FBG2半峰值带宽的变化情况，FBG1的半峰值带宽Δλ1优化值位于0.97 nm附近，两边梯度相差不大，而FBG2半峰值带宽Δλ2优化值位于1.68 nm左右，两边梯度相差不大，但明显比FBG1的梯度小很多。通过优化得出的FBG1和FBG2参数为FBG1的中心波长和半峰值带宽分别为531.0 nm和0.97 nm，FBG2的中心波长和半峰值带宽分别为528.5 nm和1.68 nm。

然后，以上述优化结果作为FBG结构参数的初始设置，以1.5 km高度的统计温度误差作为优化目标，对FBG的Bragg波长、折射率变化、光栅长度等结构参数进行优化(如图3所示)。

图3 FBG1和FBG2关键结构参数优化

图3(a)和(b)分别给出了温度误差随两个FBG的Bragg波长变化情况，图3(c)和(d)分别给出了温度误差随平均折射率变化值变化的情况，图3(e)和(f)分别给出了温度误差随光栅长度变化情况，表1给出了三个FBG优化的结构参数。

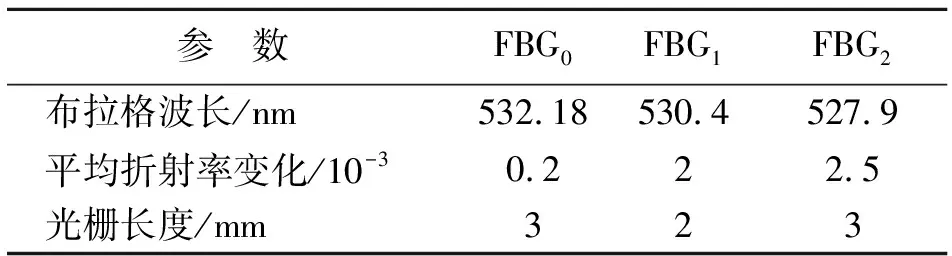
表1 全光纤转动拉曼分光系统FBG结构参数

另外，可看出Bragg波长和平均折射率变化在优化值两边误差逐渐增加，而光栅长度则变化较为平坦；6幅图的曲线变化均有振荡，这主要是由于光谱函数旁瓣与拉曼谱线的匹配效应导致的，因此在构建实验系统时最好设置相应的应变调谐机构。

4 望远镜耦合系统优化及系统性能仿真

望远镜耦合系统的效率，对全光纤拉曼测温激光雷达的实现和性能参数的评价是至关重要的。为了准确评估系统的性能参数指标，需要对耦合效率进行局部优化[12-13]。

图4(a)给出了一种耦合效率较高的结构图，L1是望远镜的等效透镜，L2是附加透镜，聚焦光路通过GRIN透镜耦合进单模光纤，可获得较高的耦合效率。增加L2的目的是调整望远镜耦合系统的实际焦距，以期对光路的耦合效率进行优化。卡塞格林望远镜的中心遮挡直径为50 mm时，不同焦距的耦合效率随高度变化的关系如图4(b)所示。从图中可看出，随着焦距变小，则近场的耦合效率越高，但是远场的耦合效率则降低，因为该系统的测量范围目前主要集中于2 km以下[7]，故选择焦距的长度为1 m。

利用美国标准大气模型数据和实测的西安大气气溶胶分布曲线，仿真得到系统的式(5)信噪比及式(6)统计温度误差曲线如图5所示。从图5可看出，考虑耦合系统耦合效率后，激光雷达的性能有所降低；1.5 km高度处未考虑耦合系统耦合效率(即耦合效率为1)时，统计温度误差为1.1 K，而考虑耦合系统耦合效率时，统计温度误差为1.3 K。

图4 望远镜耦合系统结构及其耦合效率

图5 激光雷达的信噪比及误差曲线

5 结 语

利用美国标准大气模型和西安的气溶胶后向散射测得结果，建立了全光纤转动拉曼测温激光雷达参数优化的数学模型，并以1.5 km高度的统计温度误差为优化目标，分两步实现了全光纤转动拉曼激光雷达分光系统的FBG结构参数的优化设计，最后结合望远镜耦合系统的优化结果，对系统的性能指标进行了数值仿真，结果表明设计的全光纤分光转动拉曼激光雷达系统在1.5 km高度处的统计温度误差可达1.3 K。

参考文献：

[1] Behrendt A, Reichardt J. Atmospheric temperature profiling in the presence of clouds with a pure rotational Raman lidar by use of an interference-filter based polychromator[J]. Applied Optics, 2000, 39(9): 1372-1378.

[2] 苏嘉, 张寅超, 赵曰峰, 等. 双光栅纯转动拉曼测温激光雷达单色仪的光学设计[J]. 中国激光, 2007, 34(1): 92-96.

Su Jia, Zhang Yinchao, Zhao Yuefeng, et al. Optical design of double grating monochromator of a pure rotational Raman-lidar[J]. Chinese Journal of Laser, 2007, 34(1): 92-96.

[3] Mao Jiandong, Hua Dengxin, Wang Yufeng, et al. High accuracy temperature profiling of the atmospheric boundary layer using an ultraviolet rotational Raman lidar[J]. Optics Communication, 2009, 282(15): 3113-3118.

[4] Hill K O, Meltz G. Fiber Bragg grating technology fundamentals and overview[J]. Journal of Lightwave Technology, 1997, 15(8): 1263-1276.

[5] Vann L B, DeYoung R J, Mihailov S J, et al. Narrowband fiber-optic phase-shifted Fabry-Perot Bragg grating filters for atmospheric water vapor lidar measurements[J]. Applied Optics, 2005, 44(34): 7371-7377.

[6] Mao Jiandong, Hu Liaolin, Hua Dengxin, et al. Pure rotational Raman lidar with fiber Bragg grating for temperature profiling of the atmospheric boundary layer[J]. Optica Applicata, 2008, 38(4): 715-726.

[7] 毛建东, 华灯鑫, 胡辽林, 等. 全光纤拉曼测温激光雷达分光系统设计[J]. 光学学报, 2010, 30(1): 7-13.

Mao Jiandong, Hua Dengxin, Hu Liaolin, et al. Design of spectroscopic filter of all-fiber rotational Raman lidar for temperature profiling[J]. Acta Optica Sinica, 2010, 30(1): 7-13.

[8] Erdogan T. Fiber grating spectra[J]. IEEE Journal of Lightwave Technology, 1997, 15 (8): 1277- 1294.

[9] Dikmelik Y, Davidson F M. Fiber-coupling efficiency for free-space optical communication through atmospheric turbulence[J]. Applied Optics, 2005, 44(23): 4946-4952.

[10] Li Shichun, Hua Dengxin, Wang Yufeng, et al. Analysis of telescope coupling efficiency for all-fiber spectroscopic Raman lidar[C]. 6th ISPEMI, Hangzhou, China, 2010. SPIE 7544: 75444.

[11] Hua D, Uchida M, Kobayashi T. UV Rayleigh-Mie lidar for daytime temperature profiling of the troposphere[J]. Applied Optics, 2005, 44(7): 1315-1322.

[12] 苏嘉, 张寅超, 胡顺星, 等. 多条转动拉曼谱线雷达测量对流层大气温度[J]. 光谱学与光谱分析, 2008, 28(8): 1781-1785.

Su Jia, Zhang Yinchao, Hu Shunxing, et al. Obtaining aerosol backscattering coefficient using pure rotational Raman spectrum[J]. Spectroscopy and Spectral Analysis, 2008, 28(8): 1781- 1785.

[13] 苏嘉, 张寅超, 刘玉丽, 等. 双光栅转动拉曼雷达带宽对反演大气温度的影响[J]. 大气与环境光学学报, 2007, 2(2): 114-118.

Su Jia, Zhang Yinchao, Liu Yuli, et al. Influence of bandwidth of double grating rotational Raman-lidar on atmospheric temperature’s reversion[J]. Journal of Atmospheric and Environment Optics, 2007, 2(2): 114-118.